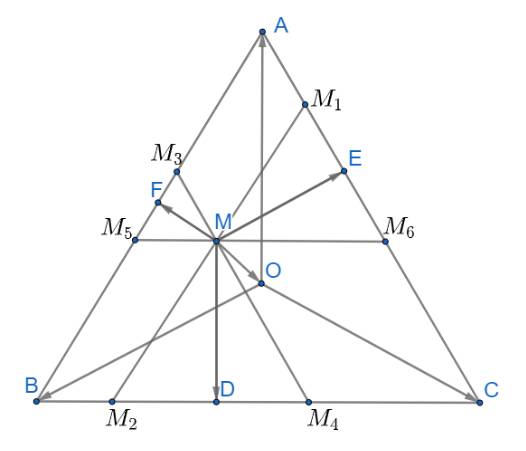
Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{2}\overrightarrow {MO} \)
\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \left( {\overrightarrow {MO} + \overrightarrow {OD} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OE} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OF} } \right)\)
Qua M kẻ các đường thẳng \({M_1}{M_2}//AB;{M_3}{M_4}//AC;{M_5}{M_6}//BC\)
Từ đó ta có: \(\widehat {M{M_1}{M_6}} = \widehat {M{M_6}{M_1}} = \widehat {M{M_4}{M_2}} = \widehat {M{M_2}{M_4}} = \widehat {M{M_3}{M_5}} = \widehat {M{M_5}{M_3}} = 60^\circ \)
Suy ra các tam giác \(\Delta M{M_3}{M_5},\Delta M{M_1}{M_6},\Delta M{M_2}{M_4}\) đều
Áp dụng tính chất trung tuyến \(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)(với M là trung điểm của BC) ta có:
\(\overrightarrow {ME} = \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right);\overrightarrow {MD} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right);\overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
\( \Rightarrow \overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
Ta có: các tứ giác \(A{M_3}M{M_1};C{M_4}M{M_6};B{M_2}M{M_5}\) là hình bình hành
Áp dụng quy tắc hình bình hành ta có
\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_3}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_5}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_4}} + \overrightarrow {M{M_6}} } \right)\)
\( = \frac{1}{2}\overrightarrow {MA} + \frac{1}{2}\overrightarrow {MB} + \frac{1}{2}\overrightarrow {MC} = \frac{1}{2}\left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)\)
\( = \frac{1}{2}\left( {\left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OC} } \right)} \right)\)
\( = \frac{1}{2}\left( {3\overrightarrow {MO} + \left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)} \right) = \frac{3}{2}\overrightarrow {MO} \) (đpcm)
Vậy \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{2}\overrightarrow {MO} \)
Đúng 0
Bình luận (0)
Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB.
Chứng minh rằng 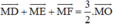
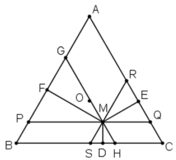
Ta có:
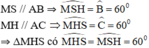
⇒ ΔMHS đều.
MD ⊥ SH nên MD là đường cao đồng thời là trung tuyến của ΔMHS.
⇒ D là trung điểm của HS
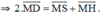
Chứng minh tương tự ta có:
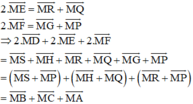
(Vì các tứ giác BSMP, HMQC, MRAG là hình bình hành)
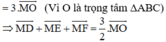
Đúng 1
Bình luận (0)
Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đền BC, AC, AB. Chứng minh rằng :
\(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}=\dfrac{3}{2}\overrightarrow{MO}\)
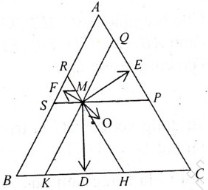
Qua M kẻ các đường thẳng song song với các cạnh của tam giác
A1B1 // AB; A2C2 // AC; B2C1 // BC.
Dễ thấy các tam giác MB1C2; MA1C1;MA2B2 đều là các tam giác đều. Ta lại có MD 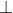 B1C2 nên MD cũng là trung điểm thuộc cạnh B1C2 của tam giác MB1C2
B1C2 nên MD cũng là trung điểm thuộc cạnh B1C2 của tam giác MB1C2
Ta có 2 =
= 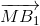 +
+ 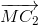
Tương tự: 2 =
= 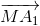 +
+ 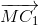
2 =
= 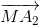 +
+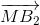
=> 2(  +
+ +
+ ) = (
) = (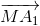 +
+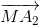 ) + (
) + (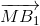 +
+ 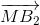 ) + (
) + (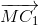 +
+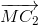 )
)
Tứ giác là hình bình hành nên
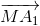 +
+ 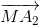 =
= 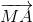
Tương tự: 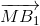 +
+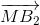 =
= 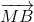
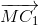 +
+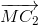 =
= 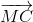
=> 2(  +
+ +
+ ) =
) = 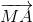 +
+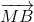 +
+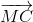
vì O là trọng tâm bất kì của tam giác và M là một điểm bất kì nên
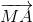 +
+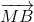 +
+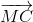 = 3
= 3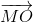 .
.
Cuối cùng ta có:
2(  +
+ +
+ ) = 3
) = 3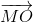 ;
;
=>  +
+ +
+ =
= 
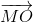
Đúng 0
Bình luận (0)
Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng :
\(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}=\dfrac{3}{2}\overrightarrow{MO}\)
Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng vecto md+me+mf=3/2mo( k dùng phương pháp kẻ song song ạ)
Cho \(\Delta ABC\) đều có O là trọng tâm và 1 điểm M tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. CMR : \(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}=\frac{3}{2}\overrightarrow{MO}\).
Cho tam giác ABC đều, M là điểm bất kì thuộc miền trong tam giác. Gọi D, E, F lần lượt là hình chiếu vuông góc của M lên các cạnh BC, AB, AC và I là tâm đường tròn nội tiếp tam giác ABC. Tìm giá trị của k biết rằng \(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}=k\overrightarrow{MI}\)
Cho tam giác ABC có
B
A
C
⏜
60
0
,
A
C
b
,
A
B
c
b
c
. Đường kính EF của đường tròn ngoại tiếp tam giác ABC vuông góc...
Đọc tiếp
Cho tam giác ABC có B A C ⏜ = 60 0 , A C = b , A B = c b > c . Đường kính EF của đường tròn ngoại tiếp tam giác ABC vuông góc với BC tại M (E thuộc cung lớn BC). Gọi I và J là chân đường vuông góc hạ từ E xuống các đường thẳng AB và AC. Gọi H và K là chân đường vuông góc hạ từ F xuống các đường thẳng AB và AC.
c) Tính độ dài cạnh BC và bán kính đường tròn ngoại tiếp tam giác ABC theo b, c.

c)
K ẻ B N ⊥ A C N ∈ A C . B A C ⏜ = 60 0 ⇒ A B N ⏜ = 30 0 ⇒ A N = A B 2 = c 2 ⇒ B N 2 = A B 2 − A N 2 = 3 c 2 4 ⇒ B C 2 = B N 2 + C N 2 = 3 c 2 4 + b − c 2 2 = b 2 + c 2 − b c ⇒ B C = b 2 + c 2 − b c
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, R là bán kính đường tròn ngoại tiếp tam giác ABC. Xét tam giác đều BCE có R = O E = 2 3 E M = 2 B C 3 3.2 = 1 3 . 3 b 2 + c 2 − b c
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC , điểm M nằm trong tam giác ABC sao cho góc MBA bằng góc MCA. Gọi D và E lần lượt là chân đường vuông góc hạ từ M xuống AB và AC , I và H lần lượt là trực tâm của tam giác ADE và ABC , P và Q lần lượt là giao điểm của DM với BH và Em với CH . CMR
a) Góc BMP bằng góc CMQ
b) Ba điểm H,I,M thẳng hàng
cho tam giác cân ABC ( AB = AC ) từ điểm M tùy ý trên cạnh BC , kẻ MD , MF lần lượt vuông góc với AB và AC kẻ đường cao BA của tam giác ABC , gọi D' là điểm đối xứng của D qua BC . Chứng minh :
a) tính góc BD'M
b) MD+MF= BH















