Question

Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đền BC, AC, AB. Chứng minh rằng :

                \(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}=\dfrac{3}{2}\overrightarrow{MO}\)

Answer 1

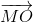
Qua M kẻ các đường thẳng song song với các cạnh của tam giác

A₁B₁ // AB; A₂C₂ // AC; B₂C₁ // BC.

Dễ thấy các tam giác MB₁C₂; MA₁C₁;MA₂B₂ đều là các tam giác đều. Ta lại có MD 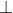B₁C₂ nên MD cũng là trung điểm thuộc cạnh B₁C₂ của tam giác MB₁C₂

Ta có 2 = +

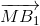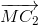
Tương tự: 2 = +

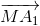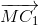
2 = +

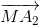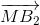
=> 2( ++) = (+) + ( + ) + (+)

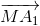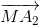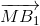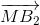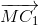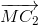Tứ giác là hình bình hành nên

+ =

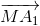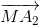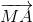
Tương tự: + =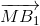

+ =

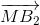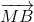
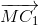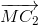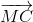
=> 2( ++) = ++

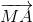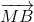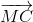
vì O là trọng tâm bất kì của tam giác và M là một điểm bất kì nên

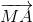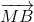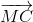++ = 3.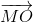

Cuối cùng ta có:

2( ++) = 3;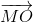

=> ++ =