a: \(=x^2-12x+36\)

b: \(=x^3+9x^2+27x+27\)

A.x=6

b.x=-3

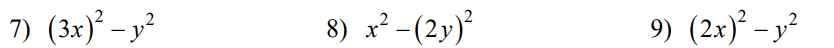
\(7)\)  \(\left(3x\right)^2-y^2=\left(3x-y\right)\left(3x+y\right)\)

\(8)\)  \(x^2-\left(2y\right)^2=\left(x-2y\right)\left(x+2y\right)\)

\(9)\)  \(\left(2x\right)^2-y^2=\left(2x-y\right)\left(2x+y\right)\)

\(a,\left(\sqrt{x}-6\right)\left(\sqrt{x}+6\right)\)

\(\sqrt{x}^2-6^2\)

\(x-36\)

\(b,\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)\)

\(\left(2\sqrt{x}\right)^2-1\)

\(4x-1\)

\(\left(\sqrt{x}-6\right)\left(6+\sqrt{x}\right)\)

\(=\left(\sqrt{x}-6\right)\left(\sqrt{x}+6\right)\)

\(=\left(\sqrt{x}\right)^2-6^2\)

\(=x-36\)

b.\(\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)\)

\(=\left(2\sqrt{x}\right)^2-1^2\)

\(=4x-1\)

Trả lời:

a, \(\left(\sqrt{x}-6\right)\left(6+\sqrt{x}\right)=\left(\sqrt{x}\right)^2-6^2=x-36\)

b, \(\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)=\left(2\sqrt{x}\right)^2-1^2=4x-1\)

a: Ta có: \(\left(x+y\right)^3-\left(x-y\right)^3\)

\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3\)

\(=6x^2y+2y^3\)

\(\left(x+y\right)^3-\left(x-y\right)^3\)

\(=\left(x+y-x+y\right)^3+3\left(x+y\right)\left(x-y\right)\left(x+y-x+y\right)\)

\(=8y^3+6y\left(x^2-y^2\right)\)

\(=8y^3+6x^2y-6y^3\)

\(=2y^3+6x^2y\)

\(=x^3+9x^2+27x+27\)

\(\left(x+y\right)^3=x^3+3x^2y+3xy^2-y^3\)

\(\left(x-y\right)^3=x^3-3x^2y+3xy^2-y^3\)

\(\left(2y-3\right)^3=8y^3-36y^2+54y-27\)

a: Ta có: \(\left(x+y\right)^3-\left(x-y\right)^3\)

\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3\)

\(=6x^2y+2y^3\)

a) \((a+y)^3=a^3+3a^2y+3ay^2+y^3\)

b) \((x-b)^3=x^3-3x^2b+3xb^2-b^3\)

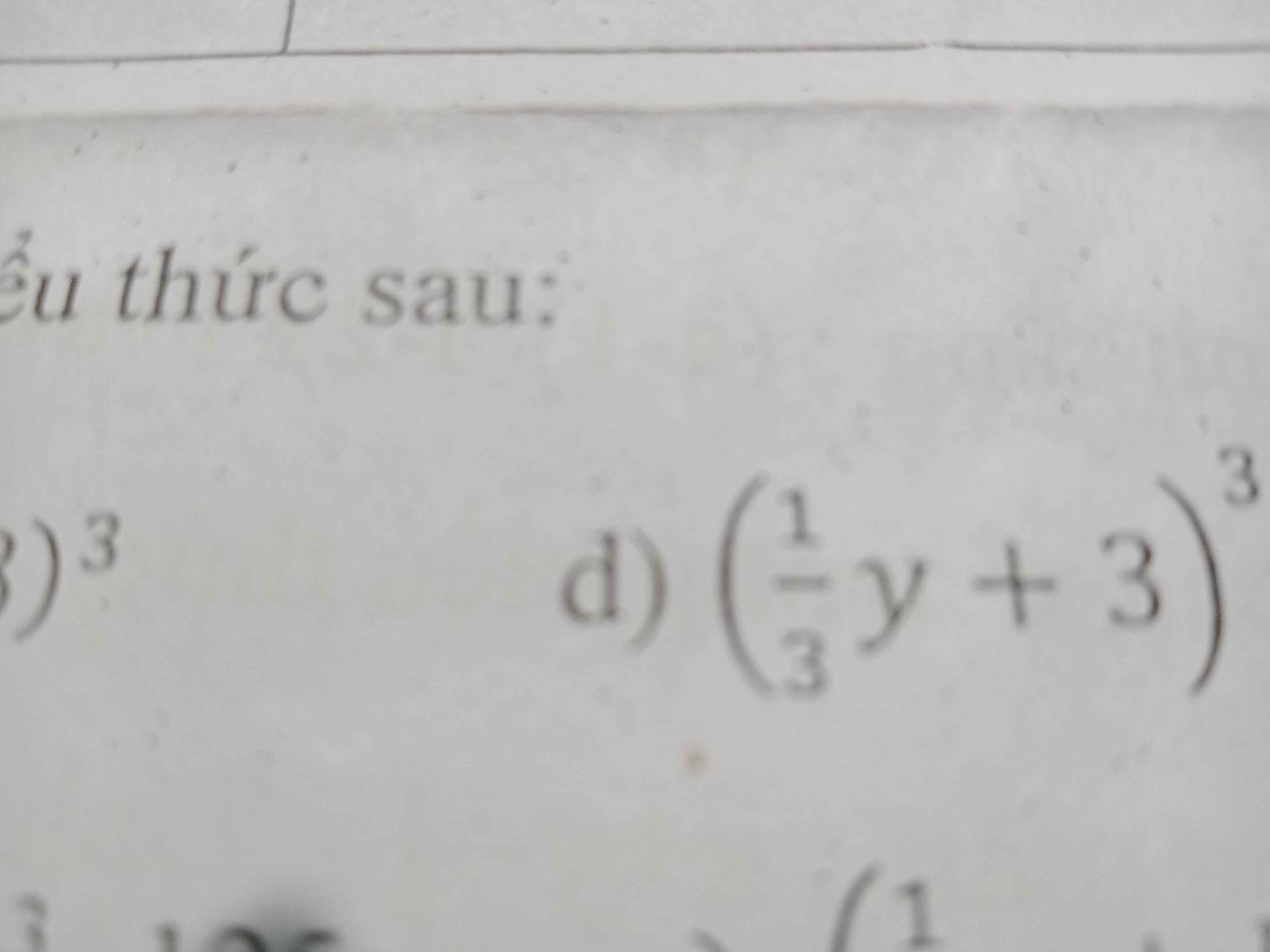
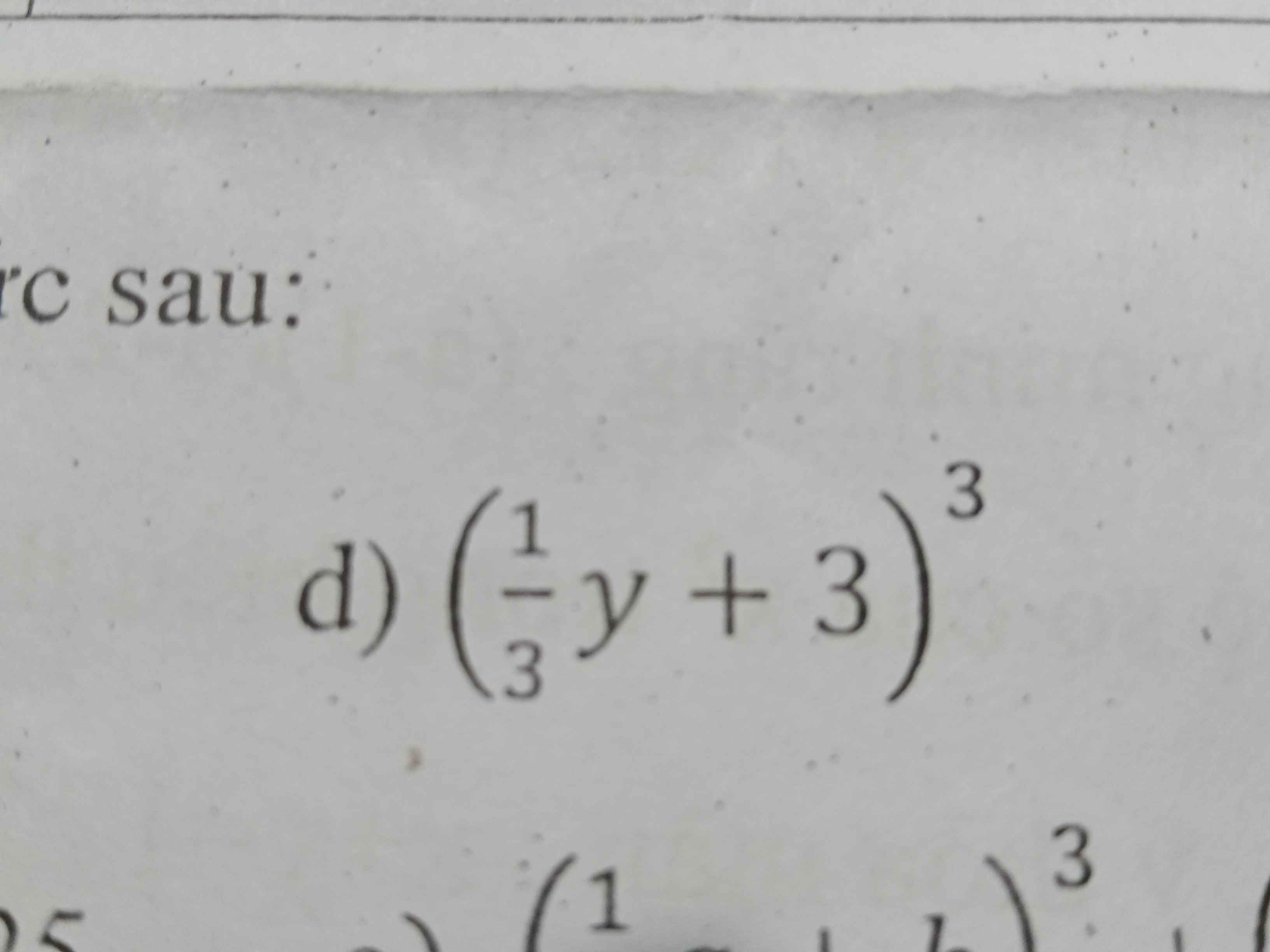
(1𝑦/3+3)^3

(𝑦/3+3)^3

(𝑦/3+3⋅3/3)^3

(𝑦+3⋅3/3)^3

(𝑦+9/3)^3

\(\left(\dfrac{1}{3}y+3\right)^3=\dfrac{1}{27}y^3+y^2+9y+27\)

\(a,\left(x+2\right)^2=x^2+4x+4\\ b,\left(x-1\right)^2=x^2-2x+1\\ c,\left(x^2+y^2\right)^2=x^4+2x^2y^2+y^4\)

a) = x² + 4x + 4

b) = x² - 2x + 1

c) x⁴ + 2x²y² + y⁴