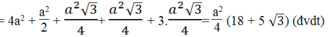Cho tam giác ABC vuông ở A có AC= 2AB; đường cao AH, trung tuyến AM. Vẽ tia phân giác At của góc BAC, vẽ đường thẳng Bx vuông với At lần lượt cắt AH, At, AM, AC ở P, I, Q, F. Vẽ Cy vuông với At tại E
a.CM: ABEF là hình thoi
b.CM: APEQ là hình thoi
Cho tam giác ABC vuông tại A và có BC = 2AB, AB = a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều AGC. Tính các góc B, C, cạnh AC và diện tích tam giác ABC.
Gọi M là trung điểm của BC, ta có:
AM = MB = 1/2 BC = a (tính chất tam giác vuông)
Suy ra MA = MB = AB = a
Suy ra ∆ AMB đều ⇒ ∠ (ABC) = 60 0
Mặt khác: ∠ (ABC) + ∠ (ACB) = 90 0 (tính chất tam giác vuông)
Suy ra: ∠ (ACB) = 90 0 - ∠ (ABC) = 90 0 – 60 0 = 30 0
Trong tam giác vuông ABC, theo Pi-ta-go, ta có: B C 2 = A B 2 + A C 2
⇒ A C 2 = B C 2 - A B 2 = 4 a 2 - a 2 = 3 a 2 ⇒ AC = a 3
Vậy S A B C = 1/2 .AB.AC
= 1 2 a . a 3 = a 2 3 2 ( đ v d t )
Cho Tam giác ABC vuông góc tại A , có BC =2AB=20cm ở phía ngoài Tam giác vẽ hình vuông BCDE, các tam giác đều ABF, ACG a, Tính góc B , góc C , cạnh AC , Diện tính ABC b, Chứng Minhh FA vg góc với BE và CG . tính Diện tính FAG và FBE
a: \(\widehat{C}=30^0\)
\(\widehat{B}=60^0\)
\(AC=\sqrt{20^2-10^2}=10\sqrt{3}\left(cm\right)\)
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=5\cdot10\sqrt{3}=50\sqrt{3}\left(cm^2\right)\)
Cho tam giác ABC vuông ở A và có BC=2AB=2a;a=17.56cm. Ở phía ngoài tam giác ABC vẽ hình vuông BCDEl, tam giác đều ABF và ACG. tính diện tích các tam giác AGF và BEF.
thiếu cái gì?
cái này chỉ là 1 phần trong bài, mấy phần kia biết làm rồi
Cho tam giác ABC vuông tại A, BC=2AB. Giải tam giác ABC biết AC=4a
Ta có:
\(sinC=\dfrac{AB}{BC}=\dfrac{AB}{2AB}=\dfrac{1}{2}\)
\(\Rightarrow\widehat{C}=30^o\)
Mà: \(\widehat{C}+\widehat{B}=90^o\Rightarrow\widehat{B}=90^o-\widehat{C}=90^o-30^o=60^o\)
Xét tam giác ABC vuông tại A có:
\(sinB=\dfrac{AC}{BC}=\dfrac{4a}{BC}\)
\(\Rightarrow BC=\dfrac{4a}{sinB}=\dfrac{4a}{sin60^o}=\dfrac{4a}{\dfrac{\sqrt{3}}{2}}=\dfrac{8a}{\sqrt{3}}=\dfrac{8\sqrt{3}a}{3}\)
\(\Rightarrow AC=\dfrac{1}{2}BC=\dfrac{1}{2}\cdot\dfrac{8\sqrt{3}}{3}=\dfrac{8\sqrt{3}}{6}a=\dfrac{4\sqrt{3}}{3}a\)
Xét ΔABC vuông tại A có sin C=AB/BC=1/2
nên góc C=30 độ
=>góc B=90-30=60 độ
Xét ΔABC vuông tại A có sin B=AC/BC
=>4a/BC=sin60
=>\(BC=4a:sin60=\dfrac{8}{3}\sqrt{3}\cdot a\)
=>\(AC=\dfrac{1}{2}\cdot BC=\dfrac{4}{3}\cdot\sqrt{3}\cdot a\)
Cho tam giác ABC vuông tại A. Có góc B = 60 độ. Tia phân giác góc B cắt AC ở D. Kẻ KC vuông góc với tia BD ở K
a) Tính số đo hóc ABD, góc ACB?
b) CMR: AB=CK
c) Tam giác AKB = Tam giác KAC
d) BC = 2AB
a
gốc BAD=30*; góc ACB=30*
b
chứng minh ▲KCB=▲ABC
=>> AB=CK
c
chứng minh tương tự như câu b
d
xét ▲ABC vuông tạ A => cos60*=AB/BC
=>> BC=2AB
Cho tam giác ABC vuông tại A có AC = 2AB . Lấy D là trung điểm của AC,Đường trung tuyến AM,cho AB=3cm tính diện tích tam giác ABM,ram giác ACN
Ta có: AC=2AB
=>\(AC=2\cdot3=6\left(\operatorname{cm}\right)\)
ΔABC vuông tại A
=>\(S_{ABC}=\frac12\cdot AB\cdot AC=\frac12\cdot3\cdot6=9\left(\operatorname{cm}^2\right)\)
M là trung điểm của BC
=>\(BM=\frac{BC}{2}\)
=>\(S_{ABM}=\frac92=4,5\left(\operatorname{cm}^2\right)\)
Cho tam giác ABC vuông tại B, có AC = 2AB. Tia phân giác của góc A cắt BC tại M, qua M kẻ đường vuông góc với AC tại H
cho tam giác abc vuông tại a có bc=2ab. tia phân giác góc b cắt ac tại .a, chứng minh bd=cd b, tính góc b và góc c của tam giác abc
a: Kẻ DK\(\perp\)BC
Xét ΔBAD vuông tại A và ΔBKD vuông tại K có
BD chung
\(\widehat{ABD}=\widehat{KBD}\)
Do đó: ΔBAD=ΔBKD
=>BA=BK
mà \(BA=\dfrac{1}{2}BC\)
nên \(BK=\dfrac{1}{2}CB\)
=>K là trung điểm của BC
Xét ΔDBC có
DK là đường cao
DK là đường trung tuyến
Do đó: ΔDBC cân tại D
b: ΔDBC cân tại D
=>\(\widehat{DBC}=\widehat{DCB}\)
mà \(\widehat{DBC}=\dfrac{1}{2}\cdot\widehat{ABC}\)
nên \(\widehat{ACB}=\dfrac{1}{2}\cdot\widehat{ABC}\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\dfrac{1}{2}\cdot\widehat{ABC}+\widehat{ABC}=90^0\)
=>\(\dfrac{3}{2}\cdot\widehat{ABC}=90^0\)
=>\(\widehat{ABC}=90^0:\dfrac{3}{2}=90^0\cdot\dfrac{2}{3}=60^0\)
\(\widehat{ACB}=\dfrac{1}{2}\cdot\widehat{ABC}=\dfrac{1}{2}\cdot60^0=30^0\)
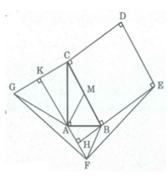
Cho tam giác ABC vuông tại A và có BC = 2AB, AB = a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều AGC. Tính diện tích tứ giác DEFG
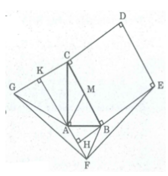
S B C D E = B C 2 = 2 a 2 = 4 a 2 (dvdt)
Trong tam giác vuông BHA, theo Pi-ta-go, ta có: A H 2 + B H 2 = A B 2
⇒ B H 2 = A B 2 - A H 2 = a 2 - a 2 / 4 = 3 a 2 / 4 ⇒ BH = (a 3 )/2
S
A
B
F
= 1/2 BH.FA = 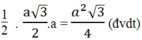
Trong tam giác vuông AKG, theo Pi-ta-go, ta có: A C 2 = A K 2 + K C 2
⇒ A K 2 = A C 2 - K C 2 = 3 a 2 - 3 a 2 / 4 = 9 a 2 / 4 ⇒ AK = 3a/2 (đvdt)
S
A
C
G
= 1/2 AK.CG = 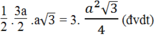
S D E F G = S B C D E + S F B E + S FAB + S F A G + S A C G + S A B C