Tham khảo:

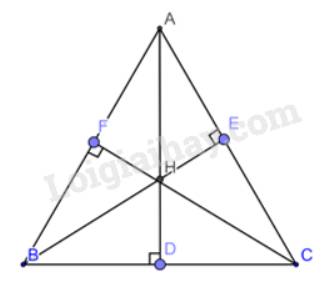
Xét tam giác BFC và tam giác BEC có :

BC chung

FC = BE

\(\widehat {BFC} = \widehat {BEC} = {90^o}\)

 ( cạnh huyền – cạnh góc vuông)

\( \Rightarrow \widehat C = \widehat B\) ( 2 góc tương ứng ) (1)

Xét tam giác CFA và tam giác ADC ta có :

CF = AD

AC chung

\(\widehat {ADC} = \widehat {AFC} = {90^o}\)

(cạnh huyền – cạnh góc vuông)

\( \Rightarrow \widehat C = \widehat A\)(2 góc tương ứng ) (2)

Từ (1) và (2) \( \Rightarrow \widehat C = \widehat A = \widehat B\) \( \Rightarrow \)Tam giác ABC là tam giác đều do có 3 góc bằng nhau 

giúp mình câu b với các bạn ơi

Xét tứ giác BFEC co góc BFC=góc BEC=90 độ

nên BFEC là tứ giác nội tiếp

Xét tứ giác MNEF có goc FME=góc FNE=90 độ

nên MNEF là tứ giác nội tiếp

=>góc AMN=góc AEF=góc ABC

=>MN//BC

b: góc HID+góc HKD=180 độ

=>HIDK nội tiếp

=>góc HIK=góc HDK

=>góc HIK=góc HCB

=>góc HIK=góc HEF

=>EF//IK

a: Xét ΔCDA vuông tại D và ΔCEB vuông tại E có

góc DCA chung

=>ΔCDA đồng dạng với ΔCEB

=>CD/CE=CA/CB

=>CD*CB=CA*CE và CD/CA=CE/CB

b; Xét ΔCDE và ΔCAB có

CD/CA=CE/CB

góc C chung

=>ΔCDE đồng dạng với ΔCAB

c:

Xét ΔCAB có

AD,BE là đường cao

AD cắt BE tại H

=>H là trực tâm

=>CH vuông góc AB tại F

góc CEB=góc CFB=90 độ

=>CEFB nội tiếp

=>góc CEF+góc CBF=180 độ

mà góc CEF+góc AEF=180 độ

nên góc AEF=góc CBA

=>góc AEF=góc CED

Theo định lý sin ta có:

\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinA=\dfrac{1}{2}\cdot4\cdot8\cdot sin30^o=8\left(cm^2\right)\)

Mà: ΔAEC vuông tại E ta có:

\(AE=sinA\cdot AC=sin30^o\cdot8=4\left(cm\right)\)

ΔABD vuông tại D nên ta có:

\(AD=sinA\cdot AB=sin30^o\cdot4=2\left(cm\right)\)

Theo định lý sin ta có:

\(S_{AED}=\dfrac{1}{2}\cdot AE\cdot AD\cdot sinA\)

\(\Rightarrow S_{AED}=\dfrac{1}{2}\cdot4\cdot2\cdot sin30^o=2\left(cm^2\right)\)

a) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có 

\(\widehat{FAC}\) chung

Do đó: ΔAEB\(\sim\)ΔAFC(g-g)

Suy ra: \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)

hay \(AE\cdot AC=AF\cdot AB\)(ĐPCM)

b)

Ta có: \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)(cmt)

nên \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)

Xét ΔAEF và ΔABC có 

\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)(cmt)

\(\widehat{FAE}\) chung

Do đó: ΔAEF\(\sim\)ΔABC(c-g-c)

d) Xét ΔBFC vuông tại F và ΔBDA vuông tại D có 

\(\widehat{FBD}\) chung

Do đó: ΔBFC\(\sim\)ΔBDA(g-g)

Suy ra: \(\dfrac{BF}{BD}=\dfrac{BC}{BA}\)(Các cặp cạnh tương ứng tỉ lệ)

hay \(BF\cdot BA=BD\cdot BC\)

Xét ΔBEC vuông tại E và ΔADC vuông tại D có 

\(\widehat{BCE}\) chung

Do đó: ΔBEC\(\sim\)ΔADC(g-g)

Suy ra: \(\dfrac{CE}{CD}=\dfrac{CB}{CA}\)(Các cặp cạnh tương ứng tỉ lệ)

hay \(CE\cdot CA=CB\cdot CD\)

Ta có: \(BF\cdot BA+CE\cdot CA\)

\(=BC\cdot BD+BC\cdot CD\)

\(=BC\left(BD+CD\right)\)

\(=BC\cdot BC=BC^2\)(Đpcm)