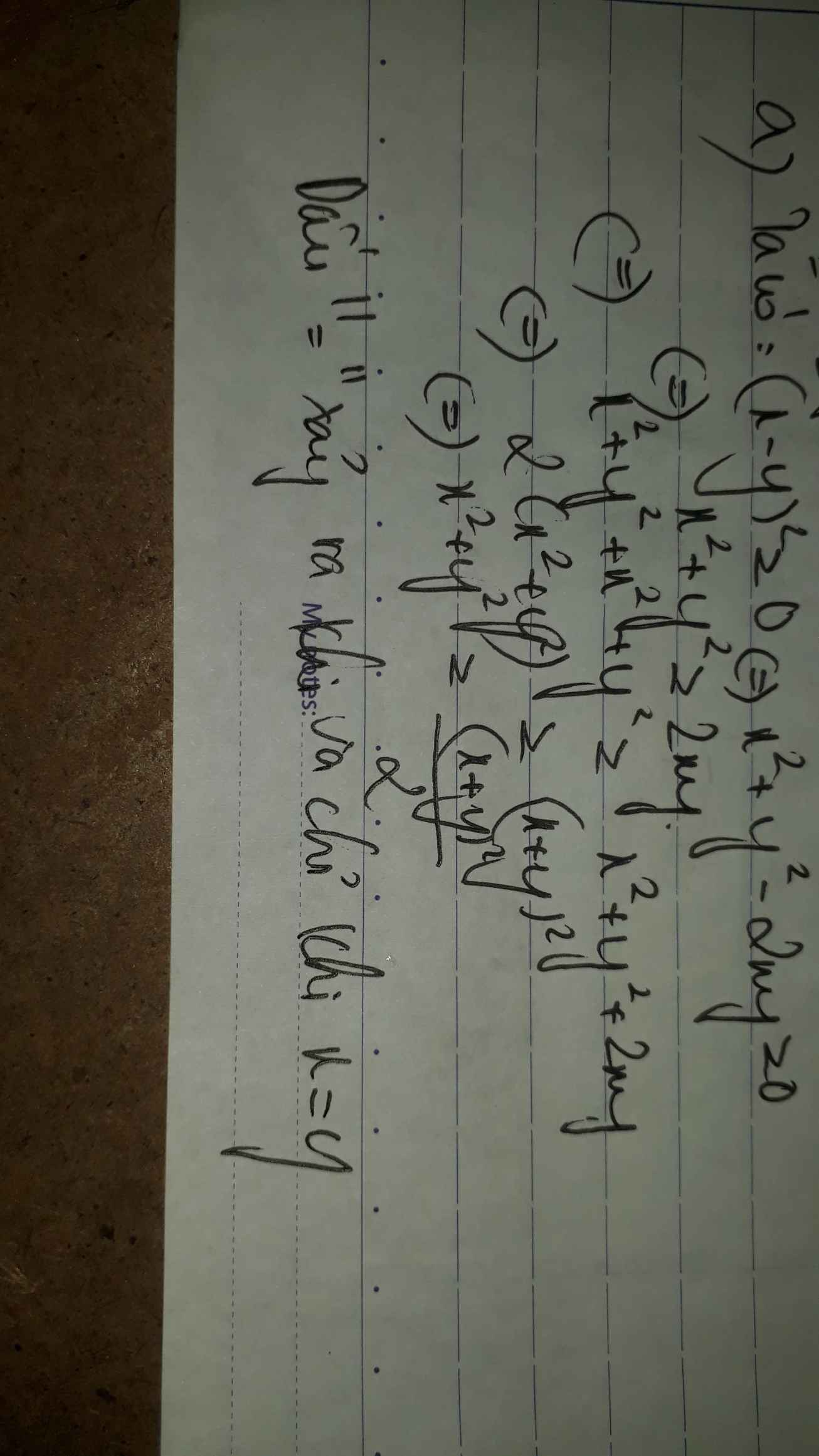a) \(x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)

\(\Leftrightarrow2x^2+2y^2\ge\left(x+y\right)^2\Leftrightarrow x^2+y^2\ge2xy\)

\(\Leftrightarrow x^2-2xy+y^2\ge0\Leftrightarrow\left(x-y\right)^2\ge0\left(đúng\right)\)

b) \(x^3+y^3\ge\dfrac{\left(x+y\right)^3}{4}\)

\(\Leftrightarrow4x^3+4y^3\ge\left(x+y\right)^3\Leftrightarrow3x^3+3y^3\ge3x^2y+3xy^2\)

\(\Leftrightarrow3x^2\left(x-y\right)-3y^2\left(x-y\right)\ge0\)

\(\Leftrightarrow3\left(x-y\right)\left(x^2-y^2\right)\ge0\Leftrightarrow3\left(x-y\right)^2\left(x+y\right)\ge0\left(đúng\right)\)

a: Ta có: \(x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)

\(\Leftrightarrow2x^2+2y^2-x^2-2xy-y^2\ge0\)

\(\Leftrightarrow x^2-2xy+y^2\ge0\)

\(\Leftrightarrow\left(x-y\right)^2\ge0\)(luôn đúng)

Dễ thấy:

     \(VT\ge\left(x+y\right)^2+1-\dfrac{\left(x+y\right)^2}{4}=\dfrac{3\left(x+y\right)^2}{4}+1\)

Áp dụng Cô-si:

     \(\dfrac{3\left(x+y\right)^2}{4}+1\ge2\sqrt{\dfrac{3\left(x+y\right)^2}{4}.1}=\sqrt{3}\left|x+y\right|\ge\sqrt{3}\left(x+y\right)\)

Do đó:

     \(\left(x+y\right)^2+1-xy\ge\sqrt{3}\left(x+y\right),\forall x,y\in R\)

bài lớp 10 bất đẳng thức mấy chú k hiểu là đúng r -______-''

hc o nha cho đó mk dg hc chi vaxma tốc độ

bài này linh tinh quá ko hiểu

giải:

-Xét hiệu 2 vế:

\(2\left(x^2+y^2\right)-\left(x+y\right)^2\)

\(=2x^2+2y^2-x^2-2xy-y^2\)

\(=x^2-2xy+y^2\)

\(=\left(x-y\right)^2\)

Xảy ra đẳng thức khi và chỉ khi x=y

-CHÚC BẠN HỌC TỐT

2(x² + y²) \(\ge\) (x + y)²

\(\Leftrightarrow\) 2(x² + y²) - (x + y)² \(\ge\) 0 (Trừ cả hai vế với (x + y)²)

\(\Leftrightarrow\) 2x² + 2y² - x² - 2xy - y² \(\ge\) 0

\(\Leftrightarrow\) x² - 2xy + y² \(\ge\) 0

\(\Leftrightarrow\) (x - y)² \(\ge\) 0

Vì (x - y)² \(\ge\) 0 nên 2(x² + y²) \(\ge\) (x + y)²

Chúc bn học tốt!!

với mọi x,y ta luôn có:
\(x^2+y^2\ge2xy\left(1\right)\)

cộng cả 2 vế bđt cho \(x^2+y^2\)

\(\left(1\right)\Leftrightarrow x^2+y^2+x^2+y^2\ge x^2+y^2+2xy\)

hay \(2\left(x^2+y^2\right)\ge\left(x+y\right)^2\)

\(\Rightarrow\)đpcm

Em thử ạ!Em không chắc đâu.Hơi quá sức em rồi

Ta có: \(VT=\Sigma\frac{x^3}{z+y+yz+1}=\Sigma\frac{x^3}{z+y+\frac{1}{x}+1}\)

\(=\Sigma\frac{x^4}{xz+xy+1+x}=\frac{x^4}{xy+xz+x+1}+\frac{y^4}{yz+xy+y+1}+\frac{z^4}{zx+yz+z+1}\)

Áp dụng BĐT Cauchy-Schwarz dạng Engel,suy ra:

\(VT\ge\frac{\left(x^2+y^2+z^2\right)^2}{\left(x+y+z\right)+2\left(xy+yz+zx\right)+3}\)

\(\ge\frac{\left(\frac{1}{3}\left(x+y+z\right)^2\right)^2}{\left(x+y+z\right)+\frac{2}{3}\left(x+y+z\right)^2+3}\) (áp dụng BĐT \(a^2+b^2+c^2\ge\frac{\left(a+b+c\right)^2}{3};ab+bc+ca\le\frac{\left(a+b+c\right)^2}{3}\))

Đặt \(t=x+y+z\ge3\sqrt{xyz}=3\) Dấu "=" xảy ra khi x = y = z

Ta cần chứng minh: \(\frac{\frac{t^4}{9}}{\frac{2}{3}t^2+t+3}\ge\frac{3}{4}\Leftrightarrow\frac{t^4}{9\left(\frac{2}{3}t^2+t+3\right)}=\frac{t^4}{6t^2+9t+27}\ge\frac{3}{4}\)(\(t\ge3\))

Thật vậy,BĐT tương đương với: \(4t^4\ge18t^2+27t+81\)

\(\Leftrightarrow3t^4-18t^2-27t+t^4-81\ge0\)

Ta có: \(VT\ge3t^4-18t^2-27t+3^4-81\)

\(=3t^4-18t^2-27t\).Cần chứng minh\(3t^4-18t^2-27t\ge0\Leftrightarrow3t^4\ge18t^2+27t\)

Thật vậy,chia hai vế cho \(t\ge3\),ta cần chứng minh \(3t^3\ge18t+27\Leftrightarrow3t^3-18t-27\ge0\)

\(\Leftrightarrow3\left(t^3-27\right)-18\left(t-3\right)\ge0\)

\(\Leftrightarrow\left(t-3\right)\left(3t^2+9t+27\right)-18\left(t-3\right)\ge0\)

\(\Leftrightarrow\left(t-3\right)\left(3t^2+9t+9\right)\ge0\)

BĐT hiển nhiên đúng,do \(t\ge3\) và \(3t^2+9t+9=3\left(t+\frac{3}{2}\right)^2+\frac{9}{4}\ge\frac{9}{4}>0\)

Dấu "=" xảy ra khi t = 3 tức là \(\hept{\begin{cases}x=y=z\\xyz=1\end{cases}}\Leftrightarrow x=y=z=1\)

Chứng minh hoàn tất

Em sửa chút cho bài làm ngắn gọn hơn.

Khúc chứng minh: \(4t^4\ge18t^2+27t+81\)

\(\Leftrightarrow4t^4-18t^2-27t-81\ge0\)

\(\Leftrightarrow\left(t-3\right)\left(4t^3+12t^2+18t+27\right)\ge0\)

BĐT hiển nhiên đúng do \(t\ge3\Rightarrow\hept{\begin{cases}t-3\ge0\\4t^3+12t^2+18t+27>0\end{cases}}\)

Còn khúc sau y chang :P Lúc làm rối quá nên không nghĩ ra ạ!

Áp dụng BĐT cosi ta có

\(\frac{x^3}{\left(1+y\right)\left(1+z\right)}+\frac{1+z}{8}+\frac{1+y}{8}\ge\frac{3}{4}x\)

\(\frac{y^3}{\left(1+x\right)\left(1+z\right)}+\frac{1+x}{8}+\frac{1+z}{8}\ge\frac{3}{4}y\)

\(\frac{z^3}{\left(1+y\right)\left(1+x\right)}+\frac{1+y}{8}+\frac{1+x}{8}\ge\frac{3}{4}z\)

Khi đó 

\(VT\ge\frac{3}{4}\left(x+y+z\right)-\frac{1}{4}\left(x+y+z\right)-\frac{3}{4}=\frac{1}{2}\left(a+b+c\right)-\frac{3}{4}\)

Mà \(x+y+z\ge3\sqrt[3]{xyz}=3\)

=> \(VT\ge\frac{3}{2}-\frac{3}{4}=\frac{3}{4}\)(ĐPCM)

Dấu bằng xảy ra khi x=y=z=1

Ô hay, em vừa tìm ra một cách chứng minh cho BĐT (2) nè:

Do x, y, z có vai trò hoán vị vòng quanh, không mất tính tổng quát giả sử \(y=min\left\{x,y,z\right\}\)

\(VT-VP=\frac{27y\left(y-z\right)^2+\left(4x+16z-11y\right)\left(y+z-2x\right)^2}{4}\ge0\)

Cái này gọi là mò:D