Cho \(\Delta\) ABC có góc BAC = 32 độ ; AB = AC = 8 cm . Vẽ góc DAC kề với góc BAC sao cho DAC = 44 độ và CD = 6 cm .
a, Tính BC
b, Tính góc ADC
c, Khoảng cách từ B đến AD ?
Cho tam giác ABC có góc BAC = 60 độ,BAC < ABC. Trong góc ABC vẽ tia Bx sao cho CBx = 60 độ.Trên tia Bx lấy điểm D sao cho BD = Bc. Trên cạnh AC lấy E sao cho AB = AE
Chứng minh rằng \(\Delta BAD=\Delta BEC\)
Lưu ý: Viết gt,kết luận và chứng minh.
Help me!
ò đợi 6h tối nay sẽ có lời giải nhá :)) Phương đi học đây
hình tự vẽ nha
Xét tam giác ABE có AB = AE => tam giác ABE cân tại A
mà góc A = 60độ => tam giác ABE là tam giác đều
=> AE = AB = BE và góc ABE = 60độ
Ta cũng có góc CBD = 60độ => góc ABE = góc CBD (1)
Ta có :
+) góc ABE = góc ABD + góc EBD (2)
+) góc CBD = góc CBE + góc EBD (3)
Từ (1)(2)(3) => góc ABD = góc CBE
Xét tam giác BAD và tam giác BEC có :
BD = BC ( gt )
góc ABD = góc CBE ( cmt )
AB = BE ( cmt )
=> tam giác BAD = tam giác BEC ( c-g-c )
=> đpcm
Cho tam giác ABC và điểm M thuộc cạnh BC thỏa mãn \(\Delta AMB = \Delta AMC\)(Hình 32). Chứng minh rằng:
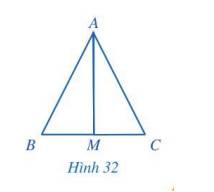
a) M là trung điểm của đoạn thẳng BC.
b) Tia AM là tia phân giác của góc BAC và \(AM \bot BC\).
a) Ta có:\(\Delta AMB = \Delta AMC\)nên AB = AC, MB = MC nên M là trung điểm của đoạn thẳng BC.
b) Ta có:\(\Delta AMB = \Delta AMC\)nên \(\widehat {AMB} = \widehat {AMC},\widehat {MAB} = \widehat {MAC},\widehat {MBA} = \widehat {MCA}\).
Vậy tia AM là tia phân giác của góc BAC vì \(\widehat {MAB} = \widehat {MAC}\).
Ta thấy:\(\widehat {AMB} = \widehat {AMC}\)mà ba điểm B, M, C thẳng hàng nên \(\widehat {BMC} = 180^\circ \).
\(\Rightarrow \widehat {AMB} = \widehat {AMC} = \dfrac{1}{2}.\widehat {BMC} = \dfrac{1}{2}.180^\circ = 90^\circ \). Vậy \(AM \bot BC\).
Cho Δ ABC , AB=15cm, góc BAC = 32 độ , góc ACB = 42 độ, đường cao AH. Tính AH, BH, HC
CÁC BÀI TOÁN VỀ QUAN HỆ TRONG 1 \(\Delta\):
Bài 1: Cho \(\Delta\)ABC có góc A=góc B=28 độ. Kẻ AD vuông góc với BC tại điểm D. Tính các góc BAD, ACB, CAD.
Bài 2: Cho \(\Delta\)ABC điểm D nằm trong A, so sánh 2 góc BAC và BDC.
Mk đang cần gấp lắm! Các bạn giải hộ mk nha!!!
\(\Delta\)ABC,góc B>C,đường cao AH và phân giác của góc BAC cắt BC tại D. Góc HAD =15 độ ; 3B=5C
Tính góc BAC
+) Tam giác AHD vuông tại H => góc ADH + HAD = 90o => ADH + 15o = 90o => góc ADH = 75o
Mà góc ADH là góc ngoài của tam giác ADC tại D nên góc ADH = DAC + C = A / 2 + C (Do AD là p/g của góc BAC)
=> A/ 2 + C = 75o => A + 2.C = 150o
Mà góc A + B + C = 180o => (A + B + C) - (A + 2.C) = 180o - 150o => B - C = 30o
Mặt khác, 3.B = 5.C => B/5 = C/3 => B/5 = C/3 = (B - C)/(5 - 3) = 30o/2 = 15o => B = 15o.5 = 75o ; C = 45o
=> góc BAC = 180o - (75o + 45o) = 60o
Dễ đối với lớp 7
khó đối với lớp < 7
Tam giác \(ABC\) có \(AB = 6cm,AC = 8cm,BC = 10cm\). Đường phân giác của góc \(BAC\) cắt cạnh \(BC\) tại \(D\).
a) Tính độ dài các đoạn thẳng \(DB\) và \(DC\).
b) Tính tỉ số diện tích giữa \(\Delta ADB\) và \(\Delta ADC\).
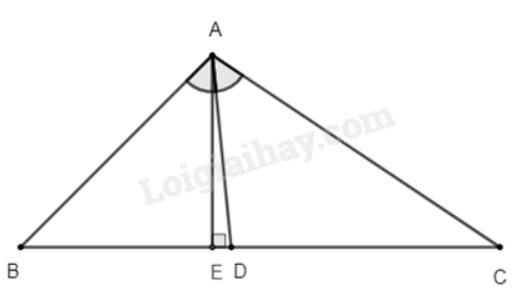
a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 10 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{10 - BD}} = \frac{6}{8} \Leftrightarrow 8BD = 6.\left( {10 - BD} \right) \Rightarrow 8BD = 60 - 6BD\)
\( \Leftrightarrow 8BD + 6BD = 60 \Leftrightarrow 14BD = 60 \Rightarrow BD = \frac{{60}}{{14}} = \frac{{30}}{7}\)
\( \Rightarrow DC = 10 - \frac{{30}}{7} = \frac{{40}}{7}\)
Vậy \(BD = \frac{{30}}{7}cm;DC = \frac{{40}}{7}cm\).
b) Kẻ \(AE \bot BC \Rightarrow AE\) là đường cao của tam giác \(ABC\).
Vì \(AE \bot BC \Rightarrow AE \bot BD \Rightarrow AE\)là đường cao của tam giác \(ADB\)
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = \frac{1}{2}BD.AE\)
Vì \(AE \bot BC \Rightarrow AE \bot DC \Rightarrow AE\)là đường cao của tam giác \(ADC\)
Diện tích tam giác \(ADC\) là:
\({S_{ADC}} = \frac{1}{2}DC.AE\)
Ta có: \(\frac{{{S_{ADB}}}}{{{S_{ADC}}}} = \frac{{\frac{1}{2}AE.BD}}{{\frac{1}{2}AE.CD}} = \frac{{BD}}{{DC}} = \frac{{\frac{{30}}{7}}}{{\frac{{40}}{7}}} = \frac{3}{4}\).
Vậy tỉ số diện tích giữa \(\Delta ADB\) và \(\Delta ADC\) là \(\frac{3}{4}\).
Cho\(\Delta\)ABC có g nửaóc B=50 độ.Trên tia đối của tia AB lấy điểm O.Trên nửa mặt phẳng bờ không chứa C bờ AB vẽ góc xOB=50 độ
a) Chứng minh rằng : Ox // BC
b) Qua A vẽ d//BC,Chứng minh rằng:góc ABC + góc BAC + góc ACB=180 độ
Cho tam giác ABC có góc BAC=60 độ và góc BAC< góc ABC .Trong tam giác ABC vẽ tia Bx sao cho góc CBx=60 độ. Trên tia Bx lấy điểm D sao cho BD=DC. CMR: AC=AB
Bài 1. Cho tam giác ABC có AB<AC. Tia phân giác của góc BAC cắt BC ở D. Trên tia AC lấy E sao cho AE=AB. Gọi M là giao điểm của AB và DE. Chứng minh rằng
a) \(\Delta ABD=\Delta AED\)
b) \(\Delta DBM=\Delta DEC\)
Lời giải:
a. Xét tam giác $ABD$ và $AED$ có:
$AB=AE$ (gt)
$\widehat{BAD}=\widehat{EAD}$ (tính chất tia phân giác)
$AD$ chung
$\Rightarrow \triangle ABD=\triangle AED$ (c.g.c)
b.
Từ tam giác bằng nhau phần a suy ra $BD=ED$ và $\widehat{ABD}=\widehat{AED}$
$\Rightarrow 180^0-\widehat{ABD}=180^0-\widehat{AED}$
$\Rightarrow \widehat{DBM}=\widehat{DEC}$
Xét tam giác $DBM$ và $DEC$ có:
$\widehat{BDM}=\widehat{EDC}$ (đối đỉnh)
$BD=ED$ (cmt)
$\widehat{DBM}=\widehat{DEC}$ (cmt)
$\Rightarrow \triangle DBM=\triangle DEC$ (g.c.g)
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: Ta có: ΔABD=ΔAED
nên \(\widehat{ABD}=\widehat{AED}\)
mà \(\widehat{MBD}=180^0-\widehat{ABD}\)
và \(\widehat{CED}=180^0-\widehat{AED}\)
nên \(\widehat{MBD}=\widehat{CED}\)
Xét ΔMBD và ΔCED có
\(\widehat{MBD}=\widehat{CED}\)
DB=DE
\(\widehat{BDM}=\widehat{EDC}\)
Do đó: ΔMBD=ΔCED
Cho hình vẽ, biết AB//DE
a) chứng minh rằng ACD=BAC+CDE
b)tính góc ACD biết góc ABC=60độ, góc CDE=32 độ
?? C lấy đâu ra vậy bạn ?