Giải chi tiết giúp mình bài này hộ với ạ
(√27 - 3√2 +2√6) : 3√3

Những câu hỏi liên quan
có ai biết giải bài này không hộ mình với mong các bạn giúp cho ( giải chi tiết hộ mình nhé, xin cảm ơn)Bài 22: rút gọn1, sqrt{3-sqrt{5}} 2, sqrt{7+3sqrt{5}}3, sqrt{9+sqrt{17}}-sqrt{9-sqrt{17}}-2Bài 26: giải các phương trình sau 1, /3-2x/2sqrt{5} →( dấu này / / là dấu giá trị tuyệt đối nha mn2, sqrt{x^2}12 3, sqrt{x^2-2x+1}7
Đọc tiếp
có ai biết giải bài này không hộ mình với mong các bạn giúp cho ( giải chi tiết hộ mình nhé, xin cảm ơn)
Bài 22: rút gọn
1, \(\sqrt{3-\sqrt{5}}\) 2, \(\sqrt{7+3\sqrt{5}}\)
3, \(\sqrt{9+\sqrt{17}}-\sqrt{9-\sqrt{17}}-2\)
Bài 26: giải các phương trình sau
1, /3-2x/=\(2\sqrt{5}\) →( dấu này '/ /' là dấu giá trị tuyệt đối nha mn
2, \(\sqrt{x^2}=12\) 3, \(\sqrt{x^2-2x+1}=7\)
có ai biết giải bài này không hộ mình với mong các bạn giúp cho ( giải chi tiết hộ mình nhé, xin cảm ơn)Bài 22: rút gọn1, sqrt{3-sqrt{5}} 2, sqrt{7+3sqrt{5}}3, sqrt{9+sqrt{17}}-sqrt{9-sqrt{17}}-sqrt{2}Bài 26: giải các phương trình sau 1, /3-2x/2sqrt{5} →( dấu này / / là dấu giá trị tuyệt đối nha mn)2, sqrt{x^2}12 3, sqrt{x^2-2x+1}74, sqrt{left(x-1right)^2}x+3
Đọc tiếp
có ai biết giải bài này không hộ mình với mong các bạn giúp cho ( giải chi tiết hộ mình nhé, xin cảm ơn)
Bài 22: rút gọn
1, \(\sqrt{3-\sqrt{5}}\) 2, \(\sqrt{7+3\sqrt{5}}\)
3, \(\sqrt{9+\sqrt{17}}-\sqrt{9-\sqrt{17}}-\sqrt{2}\)
Bài 26: giải các phương trình sau
1, /3-2x/=\(2\sqrt{5}\) →( dấu này '/ /' là dấu giá trị tuyệt đối nha mn)
2, \(\sqrt{x^2}=12\) 3, \(\sqrt{x^2-2x+1}=7\)
4, \(\sqrt{\left(x-1\right)^2}=x+3\)
22,
1, Đặt √(3-√5) = A
=> √2A=√(6-2√5)
=> √2A=√(5-2√5+1)
=> √2A=|√5 -1|
=> A=\(\dfrac{\sqrt{5}-1}{\text{√2}}\)
=> A= \(\dfrac{\sqrt{10}-\sqrt{2}}{2}\)
2, Đặt √(7+3√5) = B
=> √2B=√(14+6√5)
=> √2B=√(9+2√45+5)
=> √2B=|3+√5|
=> B= \(\dfrac{3+\sqrt{5}}{\sqrt{2}}\)
=> B= \(\dfrac{3\sqrt{2}+\sqrt{10}}{2}\)
3,
Đặt √(9+√17) - √(9-√17) -\(\sqrt{2}\)=C
=> √2C=√(18+2√17) - √(18-2√17) -\(2\)
=> √2C=√(17+2√17+1) - √(17-2√17+1) -\(2\)
=> √2C=√17+1- √17+1 -\(2\)
=> √2C=0
=> C=0
26,
|3-2x|=2\(\sqrt{5}\)
TH1: 3-2x ≥ 0 ⇔ x≤\(\dfrac{-3}{2}\)
3-2x=2\(\sqrt{5}\)
-2x=2\(\sqrt{5}\) -3
x=\(\dfrac{3-2\sqrt{5}}{2}\) (KTMĐK)
TH2: 3-2x < 0 ⇔ x>\(\dfrac{-3}{2}\)
3-2x=-2\(\sqrt{5}\)
-2x=-2√5 -3
x=\(\dfrac{3+2\sqrt{5}}{2}\) (TMĐK)
Vậy x=\(\dfrac{3+2\sqrt{5}}{2}\)
Đúng 0
Bình luận (0)
2, \(\sqrt{x^2}\)=12 ⇔ |x|=12 ⇔ x=12, -12
3, \(\sqrt{x^2-2x+1}\)=7
⇔ |x-1|=7
TH1: x-1≥0 ⇔ x≥1
x-1=7 ⇔ x=8 (TMĐK)
TH2: x-1<0 ⇔ x<1
x-1=-7 ⇔ x=-6 (TMĐK)
Vậy x=8, -6
4, \(\sqrt{\left(x-1\right)^2}\)=x+3
⇔ |x-1|=x+3
TH1: x-1≥0 ⇔ x≥1
x-1=x+3 ⇔ 0x=4 (KTM)
TH2: x-1<0 ⇔ x<1
x-1=-x-3 ⇔ 2x=-2 ⇔x=-1 (TMĐK)
Vậy x=-1
Đúng 1
Bình luận (2)
Ai giúp mình bài này với ạ!!! Giải chi tiết hộ mình nhé! Mình cảm ơn ạ!!!
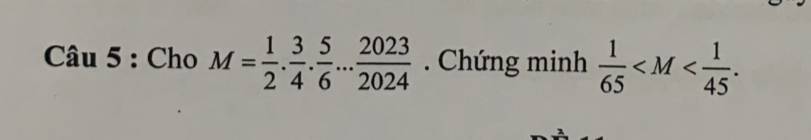
có ai biết giải ko giải hộ mình mấy bài này với ( giải chi tiết hộ mình nhé)1, 2sqrt{3+sqrt{5-sqrt{13+sqrt{48}}}}2, sqrt{6+2sqrt{5-sqrt{13+sqrt{48}}}}3, sqrt{4+sqrt{5sqrt{3+}5sqrt{48-10sqrt{7+4sqrt{3}}}}}4, sqrt{30-2sqrt{16+6sqrt{11+4sqrt{4-2sqrt{3}}}}}5, dfrac{left(5sqrt{3}+sqrt{50}right)left(5-sqrt{24}right)}{sqrt{75}-5sqrt{2}}6, sqrt{4+sqrt{8}.sqrt{2+sqrt{2}}}.sqrt{2-sqrt{2+sqrt{2}}}7, sqrt{8sqrt{3}-2sqrt{25sqrt{12}+4sqrt{192}}}
Đọc tiếp
có ai biết giải ko giải hộ mình mấy bài này với ( giải chi tiết hộ mình nhé)
1, \(2\sqrt{3+\sqrt{5-\sqrt{13+\sqrt{48}}}}\)
2, \(\sqrt{6+2\sqrt{5-\sqrt{13+\sqrt{48}}}}\)
3, \(\sqrt{4+\sqrt{5\sqrt{3+}5\sqrt{48-10\sqrt{7+4\sqrt{3}}}}}\)
4, \(\sqrt{30-2\sqrt{16+6\sqrt{11+4\sqrt{4-2\sqrt{3}}}}}\)
5, \(\dfrac{\left(5\sqrt{3}+\sqrt{50}\right)\left(5-\sqrt{24}\right)}{\sqrt{75}-5\sqrt{2}}\)
6, \(\sqrt{4+\sqrt{8}.\sqrt{2+\sqrt{2}}}.\sqrt{2-\sqrt{2+\sqrt{2}}}\)
7, \(\sqrt{8\sqrt{3}-2\sqrt{25\sqrt{12}+4\sqrt{192}}}\)
\(\sqrt{13+\sqrt{48}}=\sqrt{13+\sqrt{4.12}}=\sqrt{13+2\sqrt{12}}=\sqrt{\left(\sqrt{12}+1\right)^2}\)
\(=\sqrt{12}+1=2\sqrt{3}+1\)
\(\Rightarrow\sqrt{5-\sqrt{13+\sqrt{48}}}=\sqrt{5-2\sqrt{3}-1}=\sqrt{4-2\sqrt{3}}=\sqrt{\left(\sqrt{3}-1\right)^2}\)
\(=\sqrt{3}-1\)
\(\Rightarrow\sqrt{3+\sqrt{5-\sqrt{13+\sqrt{48}}}}=\sqrt{3+\sqrt{3}-1}=\sqrt{2+\sqrt{3}}\)
\(\Rightarrow\sqrt{\dfrac{4+2\sqrt{3}}{2}}=\sqrt{\dfrac{\left(\sqrt{3}+1\right)^2}{2}}=\dfrac{\sqrt{3}+1}{\sqrt{2}}\)
\(\Rightarrow2\sqrt{3+\sqrt{5-\sqrt{13+\sqrt{48}}}}==2.\dfrac{\sqrt{3}+1}{\sqrt{2}}=\sqrt{6}+\sqrt{2}\)
2) biến đổi khúc sau như câu 1:
\(\Rightarrow\sqrt{6+2\sqrt{5-\sqrt{13+\sqrt{48}}}}=\sqrt{6+2\left(\sqrt{3}-1\right)}=\sqrt{4+2\sqrt{3}}\)
\(=\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3}+1\)
Đúng 2
Bình luận (3)
4) Ta có: \(\sqrt{30-2\sqrt{16+6\sqrt{11+4\sqrt{4-2\sqrt{3}}}}}\)
\(=\sqrt{30-2\sqrt{16+6\sqrt{11+4\left(\sqrt{3}-1\right)}}}\)
\(=\sqrt{30-2\sqrt{16+6\sqrt{7+4\sqrt{3}}}}\)
\(=\sqrt{30-2\sqrt{16+6\left(2+\sqrt{3}\right)}}\)
\(=\sqrt{30-2\sqrt{28+6\sqrt{3}}}\)
\(=\sqrt{30-2\left(3\sqrt{3}+1\right)}\)
\(=\sqrt{28-6\sqrt{3}}=3\sqrt{3}-1\)
Đúng 1
Bình luận (0)
5) Ta có: \(\dfrac{\left(5\sqrt{3}+\sqrt{50}\right)\left(5-\sqrt{24}\right)}{\sqrt{75}-5\sqrt{2}}\)
\(=\dfrac{5\left(\sqrt{3}+\sqrt{2}\right)\left(\sqrt{3}-\sqrt{2}\right)^2}{\sqrt{75}-5\sqrt{2}}\)
\(=\dfrac{5\left(\sqrt{3}-\sqrt{2}\right)}{5\left(\sqrt{3}-\sqrt{2}\right)}=1\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời


Giải chi tiết 2 bài này giúp mình với ạ
1b
2a
3c
4b
5d
6a
7d
8b
9c
10a
--------------
1 tomb
2its
3 wonders
4 pyramid
5 reveal
6 scientific
7 found
8 ordinary
Đúng 3
Bình luận (0)

Giúp mình giải 2 bài này với ạ, giải chi tiết dùm mình nhé. Cảm ơn nhiều!!!!
2:
1+cot^2a=1/sin^2a
=>1/sin^2a=1681/81
=>sin^2a=81/1681
=>sin a=9/41
=>cosa=40/41
tan a=1:40/9=9/40
Đúng 1
Bình luận (0)

Giúp mình bài này với ạ, chi tiết càng tốt ạ <3
a: Xét ΔBAC có BI/BA=BE/BC
nên EI//AC và EI=1/2AC
=>EI vuông góc AB
DE vuông góc AB tại trung điểm của DE
=>D đối xứng E qua AB
b: Xét tứ giác DECA co
DE//CA
DE=CA(=2EI)
Do đó: DECA là hình bình hành
c: Xét tứ giác ADBE có
I là trung điểm chung của AB và DE
EA=EB
=>ADBE là hình thoi
e: Để ADBE là hình vuông thì góc AEB=90 độ
=>góc ABC=45 độ
Đúng 2
Bình luận (0)
Bạn tự vẽ hình nhé.
a) Do \(E\) đối xứng với \(D\) qua \(I\), do đó \(I\) là trung điểm của \(DE\) hay \(ID=IE\).
Ta cũng có : \(E\) là trung điểm của \(BC\), \(I\) là trung điểm của \(AB\) ⇒ \(IE\) là đường trung bình của \(\Delta ABC\) ⇒ \(IE // AC\). Lại có : \(AB\perp AC\) (giả thiết), vì vậy, \(IE\perp AB\).
Từ đó, suy ra \(AB\) là đường trung trực của \(DE\) hay \(D\) đối xứng với \(E\) qua \(AB\) (điều phải chứng minh).
b) Do \(IE\) là đường trung bình của \(\Delta ABC\) (chứng minh trên) nên \(IE=\dfrac{1}{2}AC\) và \(IE//AC\). Mặt khác, \(IE=\dfrac{1}{2}DE\). Suy ra được \(\dfrac{1}{2}AC=\dfrac{1}{2}DE\) hay \(AC=DE\). Suy ra, \(ADEC\) là hình bình hành (điều phải chứng minh).
c) Do \(I\) là trung điểm của \(DE\) (chứng minh trên) và của \(AB\) (giả thiết), suy ra \(ADBE\) là hình bình hành. Lại có \(AB\perp DE\) (do \(AB\) là đường trung trực của \(DE\) (chứng minh trên)). Suy ra, \(ADBE\) là hình thoi.
Do \(ADBE\) là hình thoi nên \(AE=EB=BD=DA=10(cm)\). Do đó, chu vi của hình thoi \(ADBE\) là \(C=AE+EB+BD+DA=4AE=4.10=40\left(cm\right)\).
d) Để hình thoi \(ADBE\) là hình vuông thì \(\hat{E}=90^o\) hay \(AE\) là đường cao của \(\Delta ABC\). Mà \(AE\) lại là đường trung tuyến của \(\Delta ABC\) (do \(E\) là trung điểm của \(BC\)). Để điều đó xảy ra thì \(\Delta ABC\) phải thêm điều kiện cân tại \(A\).
Đúng 1
Bình luận (0)
Giúp mình bài này với :(x+2)(x+5)<0
Giải chi tiết hộ mình nhé
(x + 2)(x + 5) < 0
Th1: x + 2 > 0 => x > -2
x + 5 < 0 => x < -5
=> Vô lý
Th2: x + 2 < 0 => x < -2
x + 5 > 0 => x > -5
=> -5 < x < -2
Đúng 0
Bình luận (0)
Ta có : (x+2)(x+5)<0
=> x+2 và x+5 là hai số nguyên trái dấu
mà x+5 > x+2
=> \(\hept{\begin{cases}x+5>0\\x+2< 0\end{cases}}\)
=> \(\hept{\begin{cases}x>-5\\x< 2\end{cases}}\)
=> \(-5< x< 2\)
=> \(x\in\left\{-4;-3;-2;-1;0;1\right\}\)
~ học tốt nha ~
Đúng 0
Bình luận (0)
Mọi người giải giúp mình với nha,giải chi tiết hộ mình với ạh,cảm ơn mọi người nhiều!
\(\dfrac{4x+2}{4x-2}\)+\(\dfrac{3-6x}{6x-6}\)
\(\dfrac{4x+2}{4x-2}+\dfrac{3-6x}{6x-6}\left(dkxd:x\ne\dfrac{1}{2};x\ne1\right)\)
\(=\dfrac{2\left(2x+1\right)}{2\left(2x-1\right)}+\dfrac{3\left(1-2x\right)}{6\left(x-1\right)}\)
\(=\dfrac{2x+1}{2x-1}+\dfrac{1-2x}{2\left(x-1\right)}\)
\(=\dfrac{2x+1}{2x-1}+\dfrac{1-2x}{2x-2}\)
\(=\dfrac{\left(2x+1\right)\left(2x-2\right)}{\left(2x-1\right)\left(2x-2\right)}+\dfrac{\left(1-2x\right)\left(2x-1\right)}{\left(2x-1\right)\left(2x-2\right)}\)
\(=\dfrac{4x^2-2x-2}{\left(2x-1\right)\left(2x-2\right)}+\dfrac{-4x^2+4x-1}{\left(2x-1\right)\left(2x-2\right)}\)
\(=\dfrac{4x^2-2x-2-4x^2+4x-1}{\left(2x-1\right)\left(2x-2\right)}\)
\(=\dfrac{2x-3}{\left(2x-1\right)\left(2x-2\right)}\)
\(=\dfrac{2x-3}{4x^2-6x+2}\)
Đúng 3
Bình luận (0)





















