a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)

b: ΔACB vuông tại A có AH là đường cao

nên AB^2=BH*BC

a: BC=10cm

b: Xét ΔABC vuông tại A và ΔHBA vuông tại H có

góc B chung

Do đó:ΔABC\(\sim\)ΔHBA

Suy ra: AB/HB=BC/BA=AC/HA=10/6=5/3

c: AH=4,8cm

BH=3,6cm

BẠN CÓ THỂ TRA THAY VÌ HỎI ĐC KO

thui hong cần nữa, hong cíu thì thui tui tự làm liu liu 

tham khảo

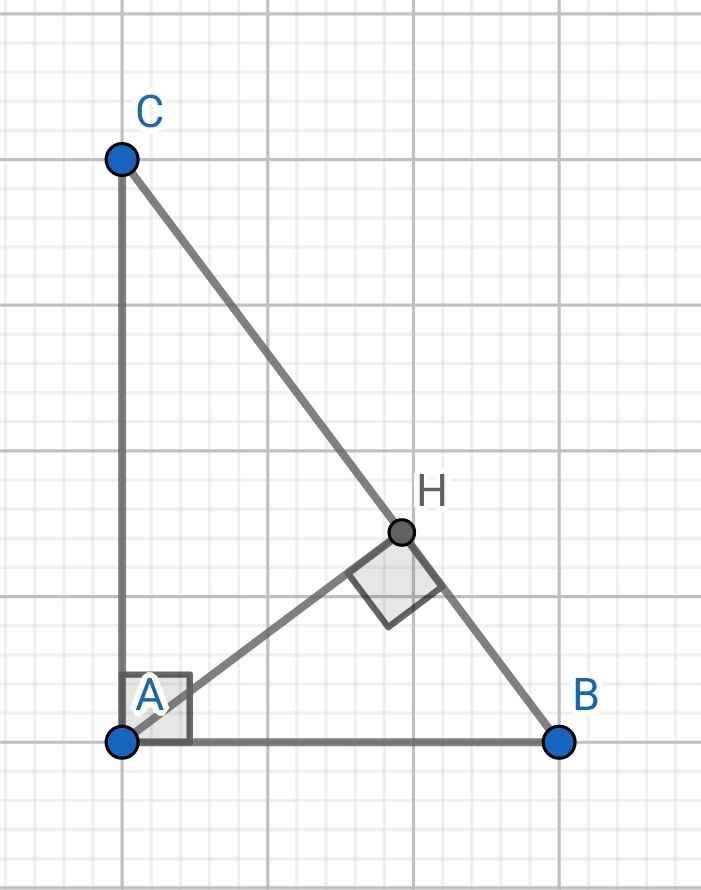
a) Xét hai tam giác vuông: ∆ABC và ∆HBA có:

∠B chung

⇒ ∆ABC ∽ ∆HBA (g-g)

b) ∆ABC vuông tại A (gt)

⇒ BC² = AB² + AC² (Pytago)

= 6² + 8²

= 100

⇒ BC = 10

Do ∆ABC ∽ ∆HBA (cmt)

⇒ AC/AH = BC/AB

⇒ AH = AB.AC/BC

= 6.8/10

= 4,8 (cm)

∆ABH vuông tại H

⇒ AB² = AH² + BH² (Pytago)

⇒ BH² = AB² - AH²

= 6² - (4,8)²

= 12,96

⇒ BH = 3,6 (cm)

a) Ta có:

- Góc A của tam giác ABC là góc vuông, nên ta có thể tính được độ dài đoạn thẳng AH bằng cách sử dụng định lí Pythagoras: AH = sqrt(AB^2 + AC^2) = sqrt(6^2 + 8^2) = 10.

- Góc A của tam giác ABC cũng là góc giữa đường cao AH và cạnh huyền BC, nên ta có thể tính được tỉ số giữa độ dài đoạn thẳng AH và độ dài cạnh huyền BC: AH/BC = AC/AB = 8/6 = 4/3.

- Từ tỉ số này, ta có thể suy ra rằng tam giác ABC đồng dạng với tam giác HBA (vì cả hai tam giác có cùng một góc và tỉ số giữa các cạnh tương ứng bằng nhau).

b) Để tính độ dài các cạnh BC, AH, BH, ta có thể sử dụng các công thức sau:

- Độ dài cạnh BC: BC = AB/AC * AH = 6/8 * 10 = 15/2 = 7.5.

- Độ dài đoạn thẳng BH: BH = sqrt(AH^2 - AB^2) = sqrt(10^2 - 6^2) = 8.

- Độ dài đoạn thẳng AH đã được tính ở trên: AH = 10.

Vậy độ dài các cạnh BC, AH, BH lần lượt là 7.5cm, 10cm, 8cm.

a) Xét ΔHBA vuông tại H và ΔABC vuông tại A có 

\(\widehat{B}\) chung

Do đó: ΔHBA\(\sim\)ΔABC(g-g)

b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=6^2+8^2=100\)

hay BC=10(cm)

Vậy: BC=10cm

b) Ta có: ΔHBA\(\sim\)ΔABC(cmt)

nên \(\dfrac{AH}{CA}=\dfrac{AB}{BC}\)(Các cặp cạnh tương ứng tỉ lệ)

hay \(\dfrac{AH}{8}=\dfrac{6}{10}=\dfrac{3}{5}\)

\(\Leftrightarrow AH=\dfrac{3\cdot8}{5}=\dfrac{24}{5}=4,8\left(cm\right)\)

Vậy: AH=4,8cm

a, \(\Delta\) HBA và \(\Delta\) ABC:

^B - chung

^H = ^A= 90⁰ => tg HBA đồng dạng ABC.

b, Vì tam giác BHA đồng dạng tg ABC:

=> \(\frac{AB}{HB}=\frac{BC}{AB}\Rightarrowđpcm\)

c, ADTC tia phân giác:

\(\Rightarrow\frac{AB}{AC}=\frac{BI}{IC}\Rightarrow\frac{BI}{AB}=\frac{IC}{AC}\)

ADTC dãy tỉ số bằng nhau 

\(\frac{BI}{AB}=\frac{IC}{AC}=\frac{BI+IC}{AB+AC}=\frac{BC}{AB+AC}=\frac{10}{6}+8=\frac{5}{7}\)

\(\Leftrightarrow\hept{\begin{cases}BI=\frac{5}{7}.6=4,3\\IC=\frac{5}{7}.8=5,7\end{cases}}\)