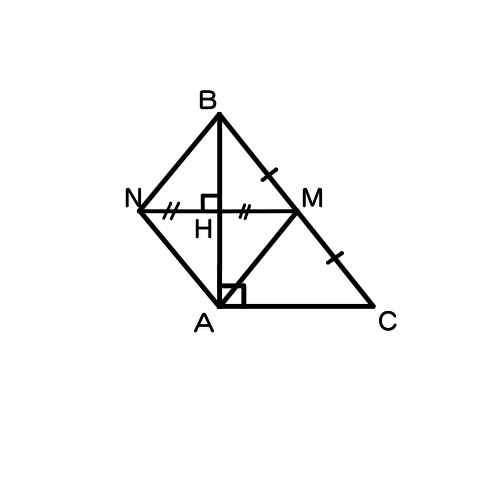
Cho hình vẽ: Trong đó HB//ME, HA//MN. Chứng minh A đối xứng với B qua O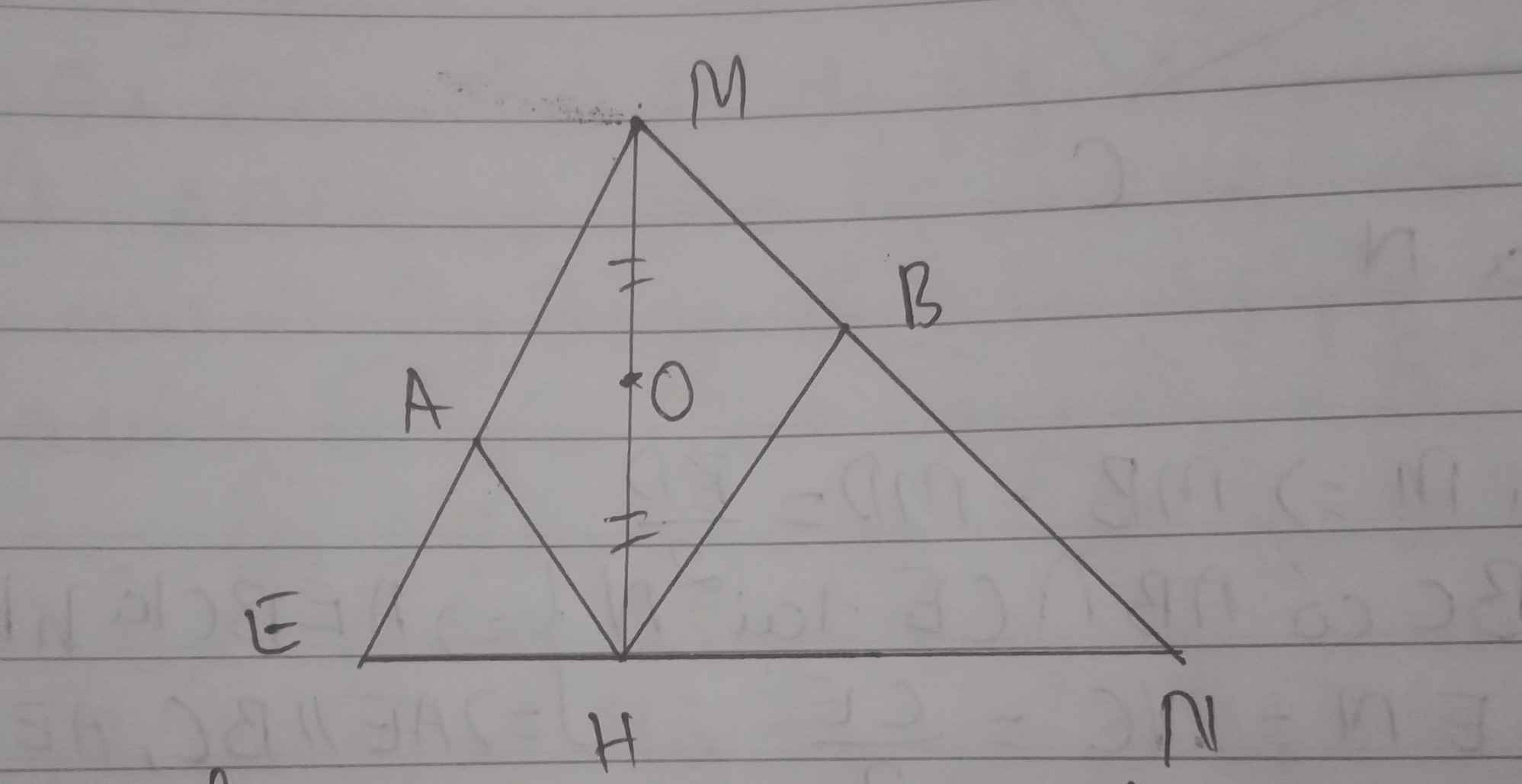

Những câu hỏi liên quan
Cho tam giác MEN, điểm H thuộc EN, O là trung điểm của MH. Biết HB//ME, HA//MN. Chứng minh rằng: A đối xứng với B qua O
Cho tam giác ABC vuông tại A , trung tuyến AM .Lấy N đối xứng với M qua AB .Gọi H là giao điểm của AB và MN . Chứng minh
a, MN//AC
b, HA=HB, MN=AC
c, ACBN là hình thang
a/ - Do N đối xứng với M qua AB => AB là đường trung trực của MN hay AB ⊥ MN
- AB ⊥ AC (△ABC vuông tại A)
=> MN // AC (đpcm)
b/ Xét △HBM và △HBN :
- HB chung
- Góc BHM = Góc BHN = 90o (gt)
- HN = HM (gt)
=> △HBM = △HBN (c.g.c)
=> BN = BM
Tứ giác ANBM có BN = BM hay hai cạnh kề bằng nhau => Tứ giác ABNM là hình thoi
Vậy : HA = HB (đpcm)
- Do tứ giác ANBM là hình thoi => AN = BM
Mà BM = CM (trung tuyến AM) => AN = MC (1)
Hình thoi ANBM có AN // BM => AN // MC (2)
Từ (1) và (2), suy ra tứ giác ANMC là hình bình hành
Vậy MN = AC (đpcm)
c/ Do AN // MB (ABNM là hình thoi), AN // MC (cmt)
=> AN // BC
Vậy: Tứ giác ACBN là hình thang (đpcm).
Đúng 0
Bình luận (0)
a) Ta có: NM⊥AB(gt)
AC⊥AB(gt)
Do đó: MN//AC(Định lí 1 từ vuông góc tới song song)
b) Xét ΔABC có
M là trung điểm của BC(gt)
MH//AC(cmt)
Do đó: H là trung điểm của AB(Định lí 1 về đường trung bình của tam giác)
Suy ra: HA=HB
Xét ΔBAC có
H là trung điểm của AB(cmt)
M là trung điểm của BC(gt)
Do đó: HM là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: \(HM=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)
mà \(HM=\dfrac{MN}{2}\)(H là trung điểm của MN)
nên AC=MN
Đúng 0
Bình luận (0)
Cho ABC nội tiếp (O) và trực tâm H. Kẻ đường kính AD a) Chứng minh rằng BHCD là hình hành b) Gọi E là điểm đối xứng của H qua O. Chứng minh rằng vecto HA + HB + HC = Vecto HE
Gọi BE, CF, AN là đường cao của TAM GIÁC ABC
Vì BE//DC⇒BH//DC(1)
CF//BD⇒CD//BH(2)
Từ (1)và(2)⇒BHCD là hình bình hành
Đúng 0
Bình luận (0)
Cho tam giác ABC nội tiếp trong đường tròn tâm O. Gọi G,H lần lượt là trọng tâm, trực tâm của tam giác ABC, D là điểm đối xứng với B qua O. a. Chứng minh AHCD là hình bình hành. Suy ra overrightarrow{HA}+overrightarrow{HB}+overrightarrow{HC}2overrightarrow{HO}. b. Chứng minh: overrightarrow{OA}+overrightarrow{OB}+overrightarrow{OC}overrightarrow{OH}. Suy ra O,G,H thẳng hàng. Giúp mình với ạ
Đọc tiếp
Cho tam giác ABC nội tiếp trong đường tròn tâm O. Gọi G,H lần lượt là trọng tâm, trực tâm của tam giác ABC, D là điểm đối xứng với B qua O. a. Chứng minh AHCD là hình bình hành. Suy ra \(\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}=2\overrightarrow{HO}\). b. Chứng minh: \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OH}\). Suy ra O,G,H thẳng hàng. Giúp mình với ạ
Cho góc xOy, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy.
a) Chứng minh rằng OB = OC
b) Tính số đo góc xOy để B đối xứng với C qua O
cho tam giác NPQ vuông tại M trong đó MA ,ME là đường trung tuyến khi là trung điểm của MQ, D đối xứng với E qua I
a, chứng minh tứ giác MEQD là hình thoi
b, vẽ K là điểm đối xứng với M qua E .chứng minh tam giác MQK vuông
BT1 : Cho hình bình hành MNPQ . Vẽ K đối xứng với N qua M . Vẽ I đối xứng với N qua P .
a) Chứng minh MPQK là hình bình hành
b) Chứng minh MPIK là hình bình hành
c) Chứng minh K đối xứng với I qua O
BT2 : Cho tam giác NMP. Lấy A thuộc MN , B thuộc MP. Qua A vẽ đường thẳng song song với MP cắt NP ở K. Qua B vẽ đường thẳng song song với MN cắt NP ở K.
a) Chứng minh AKBM là hình bình hành.
b) Chứng minh A đối xứng với B qua O với O là trung điẻm của MK .
Đọc tiếp
BT1 : Cho hình bình hành MNPQ . Vẽ K đối xứng với N qua M . Vẽ I đối xứng với N qua P .
a) Chứng minh MPQK là hình bình hành
b) Chứng minh MPIK là hình bình hành
c) Chứng minh K đối xứng với I qua O
BT2 : Cho tam giác NMP. Lấy A thuộc MN , B thuộc MP. Qua A vẽ đường thẳng song song với MP cắt NP ở K. Qua B vẽ đường thẳng song song với MN cắt NP ở K.
a) Chứng minh AKBM là hình bình hành.
b) Chứng minh A đối xứng với B qua O với O là trung điẻm của MK .
Bài 1 :
a) Vì tứ giác MNPQ là hình bình hành nên MN // QPhay MK // QP ; MN = QP
mà MN = MK ( vì K đối xứng với N qua M )
=> QP = MK và QP // MK
=> Tứ giác MPQK là hình bình hành
b) Đề sai : Sửa lại : Tứ giác MPIQ là hình bình hành
Vì tứ giác MPQK là hình bình hành nên MP = KQ
Có : PQ // NK ; PI = NP
=> QI = QK mà QK = MP nên MP = QI và MP // QI ( MP // KQ )
=> Tứ giác MPIQ là hình bình hành
c) Sửa đề nhé : \(K\) đối xứng với I qua Q
Có : KQ = QI (cmt)
=> K đối xứng với I qua Q
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, M là trung điểm của BC, vẽ N đối xứng với M qua AB. Gọi H là giao điểm của AB và MN a) c/m: MN ∥AC. b) C/m: HA = HB. c) C/m: MN = AC. d) ACMH là hình gì?
a: Ta có: N và M đối xứng nhau qua AB
nên AB là đường trung trực của MN
Suy ra: AB⊥MN tại H và H là trung điểm của MN
hay MN//AC
b: Xét ΔABC có
M là trung điểm của BC
MH//AC
Do đó: H là trung điểm của AB
hay HA=HB
Đúng 0
Bình luận (0)
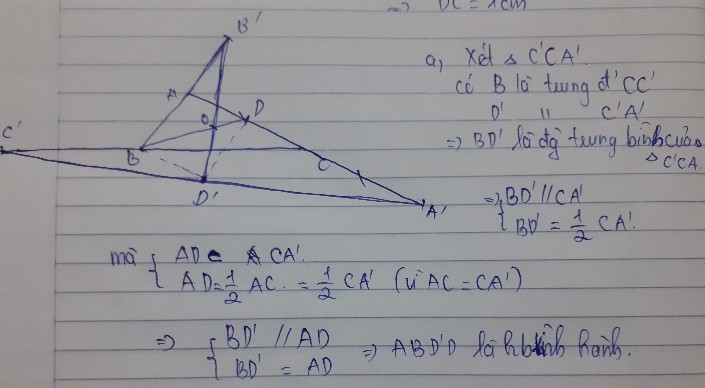
Cho tam giác ABC. vẽ A’ đối xứng với A qua C, vẽ B’ đối xứng với B qua A, vẽ C’ đối xứng với C qua B. D và D’ lần lượt là trung điểm của AC và A’C’ Chứng minh rằng ABD’D là hình bình hành Gọi O là giao điểm các trung tuyến BD và B’D’. chứng minh rằng O là trọng tâm của cả hai tam giác ABC và A’B’C’( làm ơn giúp mình, xin cảm ơn)