bạn ơi hình như thiếu đề ko có số đo tính sao dc

Mình đang cần gấp ai giải được mình k cho các bạn phải tự vẽ hình

đoạn AM chiếm 2/3 cạnh AB và cạnh AN chiếm 2/3 cạnh AC.Nên sAMN=2/3 sABC

AE đc chia làm 3 phần và AK chiếm 2 phần như thế .Nên AK nhỏ hơn AE.và AK=2/3 AE

a)   Xét   \(\Delta ABC\) và   \(\Delta HAC\) có:

\(\widehat{BAC}=\widehat{AHC}=90^0\)

\(\widehat{ABC}=\widehat{HAC}\)  do cùng phụ với góc BAH )

suy  ra:    \(\Delta ABC~\Delta HAC\)

b)  Áp dụng định lý Pytago ta có:

    \(BC^2=AB^2+AC^2\)

\(\Leftrightarrow\)\(BC^2=6^2+8^2=100\)

\(\Leftrightarrow\)\(BC=\sqrt{100}=10\)

  Áp dụng hệ thức lượng ta có:

 \(AH=\frac{AB.AC}{BC}=\frac{6.8}{10}=4,8\)cm

\(CH=\frac{AC^2}{BC}=\frac{8^2}{10}=6,4\)cm

  \(BH=BC-HC=10-6,4=3,6\)cm

\(BC\) \(\subset\)\(\left(SBC\right)\)

Tìm giao tuyến của của \(\left(OMN\right)\)và \(\left(SBC\right)\):

 \(N\)là điểm chung thứ nhất

Ta có : \(MO\)\(\subset\)\(\left(AMO\right)\)\(\equiv\)\(\left(SAH\right)\)với \(H=AO\)\(\cap\) \(BC\)

\(\left(SAH\right)\)\(\cap\) \(\left(SBC\right)\)= \(SH\)

Trong \(\left(SAH\right)\): \(MO\)\(\cap\) \(SH\)= \(K\)

\(K\)là điểm chung thứ 2.

Vậy \(\left(OMN\right)\)\(\cap\)\(\left(SBC\right)\)= \(NK\)

Trong \(\left(SBC\right):\)\(NK\)\(\cap\)\(BC\)= \(P\)

Vậy \(\left(OMN\right)\)\(\cap\) \(BC\)= \(P\)

Ta có N thuộc (OMN)

C thuộc đường thẳng BC 

Mà N trùng với C => N là giao điểm của (OMN) và BC

BC$\subset$(SBC) 

Tìm giao tuyến của (OMN) và (SBC):

  N là điểm chung thứ nhất.

Ta có: MO $\subset$ (AMO) $\equiv$ (SAH) với H= AO $\cap$ BC.

(SAH) $\cap$ (SBC) = SH

Trong (SAH): MO $\cap$ SH = K

K là điểm chung thứ 2.

Vậy  (OMN) $\cap$ (SBC) = NK

Trong (SBC): NK $\cap$ BC = P.

Vậy  (OMN) $\cap$ BC = P.

a: Xét ΔAMD và ΔCMB có

MA=MC

góc AMD=góc CMB

MD=MB

=>ΔAMD=ΔCMB

b: Xét ΔABC và ΔCDA có

AB=CD

BC=DA

AC chung

=>ΔABC=ΔCDA

c: Sửa đề: MF vuông góc BC

Xét ΔMBF và ΔMDE có

MB=MD

góc MBF=góc MDE

BF=DE

=>ΔMBF=ΔMDE

=>góc MFB=90 độ

=>MF vuông góc BC

d: ΔMFB=ΔMED

=>góc FMB=góc EMD

=>góc EMD+góc DMF=180 độ

=>M,E,F thẳng hàng

a: Xét ΔBAD và ΔBED có

BA=BE

góc ABD=góc EBD
BD chung

=>ΔBAD=ΔBED

=>AD=ED

b: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có

DA=DE

AF=EC

=>ΔDAF=ΔDEC

=>góc ADF=góc EDC

=>E,D,F thẳng hàng

c: BA=BA

DA=DE

=>BD là trung trực của AE

AD=DE
DE<DC

=>AD<DC

a)xét tg ABD và tg CBD có:

+ AB=BE(gt)

+ góc ABD = EBD (BD là phân giác)

+BD chung

=>tg ABD= tg EBD(c.gc)

b) vì tg ABD=tgEBD 

=> AD=DE và góc BAD = BED (=90 độ)

=> DE ⊥ BC

=> tg DEC có DC là cạnh huyền =>DC>ED mà ED=AD => DC>AD

c)xét tg BFE và tg BCA có:

+ Góc E = A (=90 độ)

+góc B chung

+ BE=BA

=>tg BFE =tg BCA (gcg)

=>BF=BC 

=> tg BFC cân tại B

vì S là td FC

=>BS vừa là trung tuyến vừa là đường cao

=>BS⊥FC (1)

tg BFC có: D là giao của 2 đg cao CA và FE

=> D là trực tâm => BD ⊥ FC (2)

từ 1 và 2 => B,D,S thẳng hàng

Sửa đề: AB = BE (không phải AB = AE)

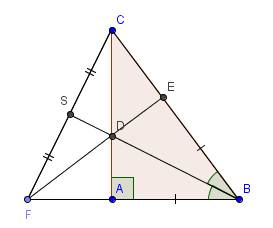
Gởi hình vẽ trước, đi công việc, tí sửa sau

Xét ∆ABD và ∆EBD có:

∠ABD = ∠EBD (do BD là phân giác của ∠B)

BD chung

AB = BE (gt)

⇒ ∆ABD = ∆EBD (c-g-c)

b) Do ∆ABD = ∆EBD (cmt)

⇒ ∠BAD = ∠BED (hai góc tương ứng)

⇒ ∠BED = 90⁰

⇒ ∠CED = 90⁰

⇒ ∆CED vuông tại E

⇒ CD là cạnh huyền nên là cạnh lớn nhất

⇒ CD > DE (1)

Do ∆ABD = ∆EBD (cmt)

⇒ AD = DE (hai cạnh tương ứng) (2)

Từ (1) và (2) ⇒ CD > AD

c) Xét hai tam giác vuông:

∆ABC và ∆EBF có:

AB = BE (gt)

∠B chung

⇒ ∆ABC = ∆EBF (cạnh góc vuông - góc nhọn kề)

⇒ BC = BF (hai cạnh tương ứng)

⇒ ∆BCF cân tại B

Lại có BD là phân giác của ∠B

⇒ BD cũng là đường trung tuyến của ∆BCF

Mà S là trung điểm FC

⇒ B, D, S thẳng hàng