Bài 1 : Cho 2 hình chữ nhật ABCD và AMNP có chung đỉnh A, đỉnh B thuộc MN và điểm P thuộc cạnh CD. CHỨng minh rằng Sabcd = Samnp

Những câu hỏi liên quan
Cho hình chữ nhật ABCD . Trên cạnh AB lấy 5 điểm và trên cạnh CD lấy 6 điểm . Nối đỉnh C và đỉnh D với mỗi điểm thuộc cạnh AB. Nối đỉnh A và đỉnh B với mỗi điểm thuộc cạnh CD . Hỏi có bao nhiêu tam giác có các đỉnh nằm trên các cạnh của hình chữ nhật được tạo thành
Cho hình chop SABCD có đáy ABCD là hình chữ nhật có độ dài cạnh AB=3a,AD=2a.Hình chiếu của đỉnh S trên mẳng phẳng đáy (ABCD) là H thuộc cạnh AB sao cho AH=2BH.Gọi M là trung điểm của cạnh BC, độ dài cạnh SCính thể tích khối chop SABCD và khoảng cách của SA và DM.
Câu hỏi của Nguyễn Bình Nguyên - Toán lớp 12 | Học trực tuyến
Đúng 0
Bình luận (1)
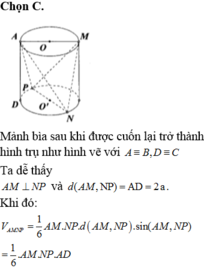
Có một mảnh bìa hình chữ nhật ABCD với AB4a, AD2a. Người ta đánh dấu M là trung điểm của AB, N và P là các điểm thuộc CD sao cho DN CP a. Sau đó người ta cuốn mảnh bìa lại sao cho cạnh BC trùng với cạnh AD tạo thành một hình trụ. Tính thể tích của tứ diện AMNP với các đỉnh A, M, N, P nằm trên hình trụ vừa tạo thành
Đọc tiếp
Có một mảnh bìa hình chữ nhật ABCD với AB=4a, AD=2a. Người ta đánh dấu M là trung điểm của AB, N và P là các điểm thuộc CD sao cho DN = CP = a. Sau đó người ta cuốn mảnh bìa lại sao cho cạnh BC trùng với cạnh AD tạo thành một hình trụ. Tính thể tích của tứ diện AMNP với các đỉnh A, M, N, P nằm trên hình trụ vừa tạo thành
![]()
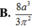
![]()
![]()
Cho hình vuông ABCD và tứ giác MNPQ có 4 đỉnh thuộc 4 cạnh của hình vuông. Chứng minh rằng: Diện tích hình vuông ABCD = AC/4 ( MN+NP+QP+QM ).
Bài 1 : Cho hình vuông ABCD có cạnh bằng 3 cm . Chứng minh rằng : 4 đỉnh của hình vuông ABCD cùng nằm trên 1 đường tròn . Hãy tính bán kính đường tròn đó Bài 2 : Cho tam giác nhọn ABC . Vẽ đường tròn tâm O , bán kính BC , nó cắt các cạnh AB, AC theo thứ tự ở D và E a)CMR: CD vuông góc với AB , BE vuông góc với AC b) gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc BCBài 3:Cho hình thang ABCD , AB//CD, ABCD , có góc Cgóc D60 độ , CD2AD . Chứng minh 4 điểm A, B, C, D cùng thuộc 1 đường trò...
Đọc tiếp
Bài 1 : Cho hình vuông ABCD có cạnh bằng 3 cm . Chứng minh rằng : 4 đỉnh của hình vuông ABCD cùng nằm trên 1 đường tròn . Hãy tính bán kính đường tròn đó
Bài 2 : Cho tam giác nhọn ABC . Vẽ đường tròn tâm O , bán kính BC , nó cắt các cạnh AB, AC theo thứ tự ở D và E
a)CMR: CD vuông góc với AB , BE vuông góc với AC
b) gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc BC
Bài 3:Cho hình thang ABCD , AB//CD, AB<CD , có góc C=góc D=60 độ , CD=2AD . Chứng minh 4 điểm A, B, C, D cùng thuộc 1 đường tròn. Tính diện tích đường tròn đó biết CD=4cm
Bài 4:Cho tam giác ABC vuông tại A. Trên AB, AC lần lượt lấy các điểm D, E . Gọi M, N, P, Q lần lượt là trung điểm của DE , EB, BC, CD. Chứng minh 4 điểm M, N, P, Q cùng thuộc 1 đường tròn
@ Trần Ngọc Huyền @ Em lần sau nhớ chia bài ra đăng nhiều lần nhé! .
Đúng 0
Bình luận (0)
Đồng ý với cô Nguyễn Thị Linh Chi
Đăng nhiều thế mới nhìn đã choáng
Cho tam giác ABC cố định. Xét các hình chữ nhật có 2 đỉnh trên cahj BC, hai đỉnh còn lại thuộc 2 cạnh kia của tam giác. Chứng minh rằng tâm của các hình chữ nhật này thuộc 1 đoạn thẳng cố định
Gọi AH là đường cao của tam giác ABC.
Gọi MNPQ là hình chữ nhật thỏa mãn điều kiện đề bài. Gọi O là tâm hình chữ nhật MNPQ.
Gọi E, F, D, G lần lượt là trung điểm của QM, PN, AH và BC. Khi đó O là trung điểm EF.
Gọi F' là giao điểm của PN và CD. Áp dụng định lý Talet ta có:
\(\frac{PF'}{AD}=\frac{FC}{CD}=\frac{F'N}{DH}\) mà AD = DH nên PF' = F'N hay F' là trung điểm của PN. Vậy F' trùng F hay F thuộc DC. Tương tự E thuộc DB.
Gọi O' là giao điểm của EF với DG. Áp dụng định lý Ta let ta có:
\(\frac{EO'}{BG}=\frac{DO'}{DG}=\frac{O'F}{GC}\) mà BG = GC nên EO' = O'F hay O' là trung điểm EF.
Từ đó suy ra O' trùng O hay O thuộc DG. Do A, B, C cố định nên DG cố định,.
Vậy tâm hình chữ nhật luôn nằm trên đoạn thẳng DG.
Đúng 0
Bình luận (0)
tâm hình chữ nhật luôn nằm trên đường thẳng dc
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 1:Chứng minh rằng trung điểm 4 cạnh của 1 hình chữ nhật là đỉnh của hình thoi
Bài 2:Chứng minh rằng trung điểm các cạnh của 1 hình thoi là đỉnh cao của 1 hình chữ nhật
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
Đúng 1
Bình luận (0)
Cho hình chữ nhật ABCD và M, N tương ứng là trung điểm của các cạnh AB, CD (H7.25). Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một hypebol có hai tiêu điểm là M và N.
Ta có: \(AM = BM = CN = DN,AN = BN = CM = DM\). Từ đó suy ra
\(\left| {AM - AN} \right| = \left| {BM - BN} \right| = \left| {CM - CN} \right| = \left| {DM - DN} \right| \).
Và \(\left| {AM - AN} \right| <MN\) (bất đẳng thức trong tam giác)
Vậy bốn điểm \(A,B,C,D\) cùng thuộc một đường hyperbol với M,N là hai tiêu điểm.
Đúng 0
Bình luận (0)
Cho hình vuông ABCD và tứ giác MNPQ có 4 đỉnh thuộc 4 cạnh của hình vuông.
a. Chứng minh rằng\(S_{ABCD}\le\frac{AC}{4}\left(MN+NP+PQ+QM\right)\)
b. Xác điịnh vị trí điểm M, N, P, Q để chu ci tứ giác MNPQ nhỏ nhất.