1) a) Cho ΔABC cân tại A, \(\widehat{B}\)=75o37'19''. Gọi I là trung điểm của AB. Tính \(\widehat{ACI}\) = ?

Những câu hỏi liên quan
1) a) Cho \(\Delta ABC\) cân tại A, \(\widehat{B}=75^o37'19''.\) Gọi I là trung điểm của AB. Tính \(\widehat{ACI}\) = ?
b) Cho \(\Delta ABC\) có AC=35cm, \(\widehat{B}=60^o\) , \(\widehat{C}=50^o\) . Tính chu vi , diện tích \(\Delta ABC\)
1.Cho ΔABC vuông tại A.widehat{B}50o.Có BC5cm,AB3cma)Tính số đo widehat{C}.Tính độ dài ACb)Gọi M là trung điểm của BC,kẻ đường thẳng d đi qua đỉnh C và song song với AB,d cắt AM tại điểm D ..CMR MAMD2.Cho ΔDFE vuông tại E.widehat{D}30o.Có DF10cm,EF6cma)Tính số đo widehat{F}.Tính độ dài DEb)Gọi I là trung điểm của DF,kẻ đường thẳng a đi qua đỉnh D và song song với EF,a cắt EI tại điểm P.CMR IEIPhộ tui tuần sau thi giữa hk II rùi
Đọc tiếp
1.
Cho ΔABC vuông tại A.\(\widehat{B}\)=50o.Có BC=5cm,AB=3cm
a)Tính số đo \(\widehat{C}\).Tính độ dài AC
b)Gọi M là trung điểm của BC,kẻ đường thẳng d đi qua đỉnh C và song song với AB,d cắt AM tại điểm D ..CMR MA=MD
2.
Cho ΔDFE vuông tại E.\(\widehat{D}\)=30o.Có DF=10cm,EF=6cm
a)Tính số đo \(\widehat{F}\).Tính độ dài DE
b)Gọi I là trung điểm của DF,kẻ đường thẳng a đi qua đỉnh D và song song với EF,a cắt EI tại điểm P.CMR IE=IP
hộ tui tuần sau thi giữa hk II rùi
1.Cho ΔABC vuông tại A.widehat{B}50o.Có BC5cm,AB3cma)Tính số đo widehat{C}.Tính độ dài ACb)Gọi M là trung điểm của BC,kẻ đường thẳng d đi qua đỉnh C và song song với AB,d cắt AM tại điểm D ..CMR MAMD2.Cho ΔDFE vuông tại E.widehat{D}30o.Có DF10cm,EF6cma)Tính số đo widehat{F}.Tính độ dài DEb)Gọi I là trung điểm của DF,kẻ đường thẳng a đi qua đỉnh D và song song với EF,a cắt EI tại điểm P.CMR IEIPhộ tui tuần sau thi giữa hk II rùi
Đọc tiếp
1.
Cho ΔABC vuông tại A.\(\widehat{B}\)=50o.Có BC=5cm,AB=3cm
a)Tính số đo \(\widehat{C}\).Tính độ dài AC
b)Gọi M là trung điểm của BC,kẻ đường thẳng d đi qua đỉnh C và song song với AB,d cắt AM tại điểm D ..CMR MA=MD
2.
Cho ΔDFE vuông tại E.\(\widehat{D}\)=30o.Có DF=10cm,EF=6cm
a)Tính số đo \(\widehat{F}\).Tính độ dài DE
b)Gọi I là trung điểm của DF,kẻ đường thẳng a đi qua đỉnh D và song song với EF,a cắt EI tại điểm P.CMR IE=IP
hộ tui tuần sau thi giữa hk II rùi
Câu 2:
a: ΔDEF vuông tại E
=>\(\widehat{EDF}+\widehat{EFD}=90^0\)
=>\(\widehat{EFD}+30^0=90^0\)
=>\(\widehat{EFD}=60^0\)
ΔDEF vuông tại E
=>\(ED^2+EF^2=FD^2\)
=>\(ED^2=10^2-6^2=64\)
=>\(ED=\sqrt{64}=8\left(cm\right)\)
b: Xét ΔIFE và ΔIDP có
\(\widehat{IFE}=\widehat{IDP}\)(hai góc so le trong, EF//DP)
IF=ID
\(\widehat{FIE}=\widehat{DIP}\)(hai góc đối đỉnh)
Do đó: ΔIFE=ΔIDP
=>IE=IP
Câu 1:
a: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=90^0-50^0=40^0\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=5^2-3^2=16\)
=>\(AC=\sqrt{16}=4\left(cm\right)\)
b: Xét ΔMAB và ΔMDC có
\(\widehat{MBA}=\widehat{MCD}\)(hai góc so le trong, BA//CD)
MB=MC
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
Do đó: ΔMAB=ΔMDC
=>MA=MD
Đúng 0
Bình luận (0)
Cho tam giác \(ABC\) cân tại \(A\) có \(\widehat{B}=75^o57'19''\). Gọi \(M\) là trung điểm của \(AB\). Tính \(\widehat{ACM}?\) làm tròn đến giây.
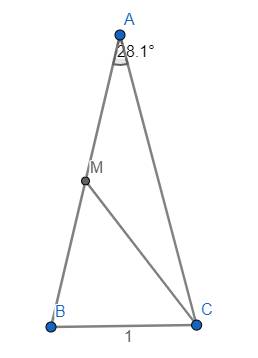
Không mất tổng quát, giả sử \(BC=1\).
Từ gt \(\Rightarrow\widehat{BAC}=180^o-2\widehat{ABC}=28^o5'22''\)
Áp dụng định lý sin cho tam giác ABC, ta có:
\(\dfrac{AC}{\sin B}=\dfrac{BC}{\sin A}\Rightarrow AC=\dfrac{BC\sin B}{\sin A}\) \(=\dfrac{\sin\left(75^o57'19''\right)}{\sin\left(28^o5'22''\right)}=2k\)
Mà tam giác ABC cân tại A nên \(AB=AC=2k\)
\(\Rightarrow MB=MA=k\)
Có \(MC=\sqrt{\dfrac{2\left(CA^2+CB^2\right)-AB^2}{4}}\) \(=\sqrt{\dfrac{2\left(4k^2+1\right)-4k^2}{4}}\) \(=\dfrac{\sqrt{4k^2+2}}{2}\) (Công thức tính độ dài đường trung tuyến trong tam giác, mình không chứng minh ở đây nhé.)
Áp dụng định lý sin cho tam giác ACM, có:
\(\dfrac{AM}{\sin\widehat{ACM}}=\dfrac{CM}{\sin\widehat{A}}\) \(\Rightarrow\sin\widehat{ACM}=\dfrac{AM\sin A}{CM}\) \(=\dfrac{k\sin\left(28^o5'22''\right)}{\dfrac{\sqrt{4k^2+2}}{2}}\)
\(\Rightarrow...\)
Đúng 2
Bình luận (0)
1)cho tam giác ABC vuông cân tại A. M là trung điểm của BC. G thuộc AB sao cgo AGfrac{1}{3}AB, E là chân đường vuông góc hạ từ M xuống CG. MG và AC cắt nhau tại D. so sánh DE và BC2) cho tam giác ABC vuông tại A và widehat{BAC} 60 , M thuộc BC sao cho AB+BMAC+CM. tínhwidehat{CAM}3) cho tam giác ABC cân tại A , gọi E là điểm bất kì nằm giữa B và C , đường thẳng qua E vuông góc với AB và đường thẳng qua C vuông góc với AC cắt nhau tại D. gọi K là trung điểm của BE. tính widehat{AKD}4)cho tam giác...
Đọc tiếp
1)cho tam giác ABC vuông cân tại A. M là trung điểm của BC. G thuộc AB sao cgo AG=\(\frac{1}{3}\)AB, E là chân đường vuông góc hạ từ M xuống CG. MG và AC cắt nhau tại D. so sánh DE và BC
2) cho tam giác ABC vuông tại A và \(\widehat{BAC}\)= 60' , M thuộc BC sao cho AB+BM=AC+CM. tính\(\widehat{CAM}\)
3) cho tam giác ABC cân tại A , gọi E là điểm bất kì nằm giữa B và C , đường thẳng qua E vuông góc với AB và đường thẳng qua C vuông góc với AC cắt nhau tại D. gọi K là trung điểm của BE. tính \(\widehat{AKD}\)
4)cho tam giác ABC cân tại A. trên đường thẳng AC lấy điểm M tùy ý.đường thẳng vuông góc với BC qua M cắt BC tại H. gọi I là trung điểm của BM. tính\(\widehat{HAI}\)
Cho tam giác ABC cân tại A có \(\widehat A = {56^o}\)(Hình 15)
a) Tính\(\widehat B\), \(\widehat C\)
b) Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng tam giác AMN cân.
c) Chứng minh rằng MN // BC
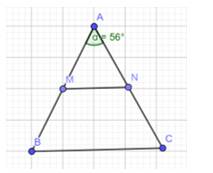
a) Theo đề bài ta có tam giác ABC cân ở A và \(\widehat A = {56^o}\)
Mà \( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat B = \widehat C = ({180^o} - {56^o}):2 = {62^o}\)
b) Vì tam giác ABC cân tại A nên AB = AC ( định nghĩa tam giác cân )
Mà M, N là trung điểm của AB, AC
Nên AM = AN
Xét tam giác AMN có AM = AN nên AMN là tam giác cân tại A
\( \Rightarrow \widehat M = \widehat N = ({180^o} - {56^o}):2 = {62^o}\)
c) Vì \(\widehat {AMN}=\widehat {ABC}\) (cùng bằng 62°)
Mà chúng ở vị trí đồng vị nên MN⫽BC
Đúng 0
Bình luận (0)
Bài 1 : Cho hình thang ABCD (AB//CD), widehat{A}widehat{D}90o , AB11cm , AD 12 cm, Bc 13 cm . Tính ACBài 2 : Cho ΔABC cân tại A. Trên cạnh AB,AC lấy điểm M,N sao cho BM CNa)Tứ giác BMNC là hình gì ? Vì sao ?b)Tính các góc của tứ giác BMNC biết rằng widehat{A} bằng 40o
Đọc tiếp
Bài 1 : Cho hình thang ABCD (AB//CD), \(\widehat{A}\)=\(\widehat{D}\)=90o , AB=11cm , AD= 12 cm, Bc = 13 cm . Tính AC
Bài 2 : Cho ΔABC cân tại A. Trên cạnh AB,AC lấy điểm M,N sao cho BM = CN
a)Tứ giác BMNC là hình gì ? Vì sao ?
b)Tính các góc của tứ giác BMNC biết rằng \(\widehat{A}\) bằng 40o
Bài 2:
a) Xét ΔABC có
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\left(AM=AN;AB=AC\right)\)
Do đó: MN//BC(Định lí Ta lét đảo)
Xét tứ giác BMNC có MN//BC(gt)
nên BMNC là hình thang có hai đáy là MN và BC(Định nghĩa hình thang)
Hình thang BMNC có \(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
nên BMNC là hình thang cân(Dấu hiệu nhận biết hình thang cân)
Đúng 1
Bình luận (0)
Cho ΔABC vuông tại A, biết AB 6cm; AC 8cm. a) Tính độ dài cạnh BC, so sánh widehat{B} và widehat{C}. b) Vẽ trung tuyến AM của ΔABC. Trên tia đối của tia MA lấy điểm E sao cho ME MA. Chứng minh: ΔMAB ΔMEC và widehat{ACE} 90 độ. c) Gọi H là trung điểm của cạnh AC, chứng minh: HB HE. d) HB cắt AE tại P, HE cắt BC tại Q, chứng minh: ΔHPQ cân.
Đọc tiếp
Cho ΔABC vuông tại A, biết AB = 6cm; AC = 8cm.
a) Tính độ dài cạnh BC, so sánh \(\widehat{B}\) và \(\widehat{C}\).
b) Vẽ trung tuyến AM của ΔABC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh: ΔMAB = ΔMEC và \(\widehat{ACE}\) = 90 độ.
c) Gọi H là trung điểm của cạnh AC, chứng minh: HB = HE.
d) HB cắt AE tại P, HE cắt BC tại Q, chứng minh: ΔHPQ cân.
Cho ΔABC vuông tại A (AB < AC), đường cao AH. Trên cạnh AC lấy điểm D sao cho AD = AB. Gọi O là trung điểm của BD. . Vẽ (O) đường kính BD cắt cạnh BC tại điểm thứ hai K.
a, C/m: A thuộc đường tròn (O)
b, C/m: \(\widehat{AKB}=\widehat{ADB}\)
c, C/m: CK.CB = CD.CA
d, Tính \(\widehat{AHO}\)
a) Ta có: ΔABD vuông tại A(gt)
nên A nằm trên đường tròn đường kính BD(Định lí quỹ tích cung chứa góc)
mà BD là đường kính của (O)
nên A\(\in\)(O)(Đpcm)
Đúng 0
Bình luận (0)
b) Xét (O) có
\(\widehat{AKB}\) là góc nội tiếp chắn cung AB
\(\widehat{ADB}\) là góc nội tiếp chắn cung AB
Do đó: \(\widehat{AKB}=\widehat{ADB}\)(Hệ quả góc nội tiếp)
Đúng 0
Bình luận (0)
















