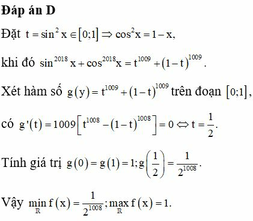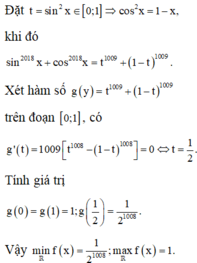sin2018x + cos2018x = 1. Giải phương trình lượng giác

Những câu hỏi liên quan
Cho phương trình
sin
2018
x
+
cos
2018
x
2
sin
2020
x
+
cos
2020
x
. Tính tổng các nghiệm của phương trình trong khoảng (0;2018)
Đọc tiếp
Cho phương trình sin 2018 x + cos 2018 x = 2 sin 2020 x + cos 2020 x . Tính tổng các nghiệm của phương trình trong khoảng (0;2018)
![]()
![]()
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
f
x
sin
2018
x
+
cos
2018
x
trên tập
R
. Khi đó
Đọc tiếp
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f x = sin 2018 x + cos 2018 x trên tập R . Khi đó
![]()
![]()
![]()
![]()
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
f
x
sin
2018
x
+
cos
2018
x
trên tập R. Khi đó A.
M
2
;
m
1
2
1018
B.
M
2
;
m...
Đọc tiếp
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f x = sin 2018 x + cos 2018 x trên tập R. Khi đó
A. M = 2 ; m = 1 2 1018
B. M = 2 ; m = 1 2 1019
C. M = 1; m = 0
D. M = 1 ; m = 1 2 1018
Gọi M,m lần lươt là trị lớn nhất trị lớn nhất, nhỏ nhất của hàm số f(x)
sin
2018
x
+
cos
2018
x
trên tập
ℝ
. Khi đó A. B. C. D.
Đọc tiếp
Gọi M,m lần lươt là trị lớn nhất trị lớn nhất, nhỏ nhất của hàm số f(x)= sin 2018 x + cos 2018 x trên tập ℝ . Khi đó
A. 
B. ![]()
C. ![]()
D. 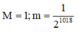
giải phương trình lượng giác Sin(cosx)=1
=>cosx=pi/2+k2pi
Phương trình này sẽ có nghiệm khi -1<=pi/2+k2pi<=1 và k thuộc Z
=>\(x\in\varnothing\)
Đúng 0
Bình luận (0)
Giải phương trình lượng giác sau:
\(\dfrac{cos2x}{1-sinx}=0\)
Để giải phương trình cos(2x) - sin(x) = 0, ta có thể sử dụng các công thức lượng giác để đưa phương trình về dạng phù hợp.
Bước 1: Sử dụng công thức cos(2x) = 2cos^2(x) - 1, phương trình trở thành 2cos^2(x) - 1 - sin(x) = 0.
Bước 2: Sử dụng công thức sin^2(x) + cos^2(x) = 1, ta có thể thay thế cos^2(x) bằng 1 - sin^2(x), phương trình trở thành 2(1 - sin^2(x)) - 1 - sin(x) = 0.
Bước 3: Giải phương trình 2 - 2sin^2(x) - 1 - sin(x) = 0.
Bước 4: Đặt sin(x) = t, phương trình trở thành 2 - 2t^2 - 1 - t = 0.
Bước 5: Rút gọn phương trình, ta có -2t^2 - t + 1 = 0.
Bước 6: Giải phương trình bậc hai trên, ta có thể sử dụng công thức hoặc phân tích thành nhân tử để tìm giá trị của t.
Bước 7: Giải phương trình -2t^2 - t + 1 = 0, ta tìm được hai giá trị t = -1 và t = 1/2.
Bước 8: Đặt sin(x) = -1 và sin(x) = 1/2, ta tìm được hai giá trị x = -π/2 và x = π/6.
Vậy, phương trình cos(2x) - sin(x) = 0 có hai nghiệm là x = -π/2 và x = π/6.
Đúng 0
Bình luận (0)
ĐKXĐ: 1-sin x<>0
=>sin x<>1
=>x<>pi/2+k2pi
cos2x/1-sinx=0
=>cos2x=0
=>2x=pi/2+kpi
=>x=pi/2+kpi/2
Kết hợp ĐKXĐ, ta được: \(x\in\left\{pi+k2pi;\dfrac{3}{2}pi+k2pi;2pi+k2pi\right\}\)
Đúng 0
Bình luận (0)
Nêu cách giải phương trình lượng giác cơ bản , cách giải phương trình a sin x + b cos x = c .
a) Cách giải các phương trình lượng giác cơ bản:
+ Phương trình sin x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho sin α = a.
Khi đó phương trình trở thành sin x = sin α
⇒ Phương trình có nghiệm: 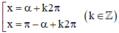
+ Phương trình cos x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho cos α = a.
Khi đó phương trình trở thành cos x = cos α.
⇒ Phương trình có nghiệm: x = ±α + k2π (k ∈ Z).
+ Phương trình tan x = a.
Tìm một cung α sao cho tan α = a.
Khi đó phương trình trở thành tan x = tan α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
+ Phương trình cot x = a
Tìm một cung α sao cho cot α = a.
Khi đó phương trình trở thành cot x = cot α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
b) Cách giải phương trình a.sin x + b.cos x = c.
+ Nếu a = 0 hoặc b = 0 ⇒ Phương trình lượng giác cơ bản .
+ a ≠ 0 và b ≠ 0. Chia cả hai vế của phương trình cho  ta được:
ta được:

Ta giải phương trình trên như phương trình lượng giác cơ bản.
Đúng 0
Bình luận (0)
Giải phương trình lượng giác
`sin(8x+60^o)+sin2x=0`
`<=> sin(8x+60^o) = -sin2x`
`<=> sin(8x+60^o) = sin(-2x)`
\(\Leftrightarrow\left[{}\begin{matrix}8x+60^o=-2x+k.360^o\\8x+60^o=180^o+2x+k.360^o\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-6^o+36^o.k\\x=20^o+60^o.k\end{matrix}\right.\)
Vậy....
Đúng 1
Bình luận (0)
Giải phương trình lượng giác sau :2cos(2x+pi/3)+2cosx-1=0
giải phương trình lượng giác
\(\dfrac{cosx-\sqrt{3}sinx}{sinx-\dfrac{1}{2}}=0\)
ĐK: \(x\ne\dfrac{\pi}{6}+k2\pi;x\ne\dfrac{5\pi}{6}+k2\pi\)
\(\dfrac{cosx-\sqrt{3}sinx}{sinx-\dfrac{1}{2}}=0\)
\(\Leftrightarrow cosx-\sqrt{3}sinx=0\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=0\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=0\)
\(\Leftrightarrow x+\dfrac{\pi}{3}=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\)
Đối chiếu điều kiện ta được \(x=-\dfrac{5\pi}{6}+k2\pi\).
Đúng 0
Bình luận (0)