CM: ABC vuông tại A

cho tam giác ABC vuông tại A . Đường cao AH. HM vuông góc với AB tại M . HN vuông góc với AC tại N . Kẻ M đến N .biết PAMN=14(cm) ,PABC=28(cm).tính góc ABC
Kí hiệu \(P_{AMN}\) ở đây nghĩa là gì em nhỉ? Chắc là chu vi tam giác?
Tứ giác AMHN là hình chữ nhật (có 3 góc vuông) \(\Rightarrow\widehat{BAH}=\widehat{AMN}\)
Mà \(\widehat{BAH}=\widehat{ACB}\) (cùng phụ \(\widehat{ABC}\))
\(\Rightarrow\widehat{AMN}=\widehat{ACB}\)
\(\Rightarrow\Delta_vAMN\sim\Delta_VACB\) (g.g)
\(\Rightarrow\dfrac{AM}{AC}=\dfrac{AN}{AB}=\dfrac{MN}{BC}=\dfrac{AM+AN+MN}{AC+AB+BC}=\dfrac{14}{28}=\dfrac{1}{2}\)
Mà \(MN=AH\) (hai đường chéo hình chữ nhật)
\(\Rightarrow BC=2AH\)
Gọi K là trung điểm BC \(\Rightarrow BC=2AK\) (trung tuyến ứng với cạnh huyền bằng 1 nửa cạnh huyền)
\(\Rightarrow\) H trùng K \(\Rightarrow AH\) vừa là đường cao vừa là trung tuyến
\(\Rightarrow\Delta ABC\) vuông cân tại A
\(\Rightarrow\widehat{ABC}=45^0\)
Cho tam giác ABC, đường cao AM.
a) Biết tam giác ABC vuông tại A, AB : BC = 3 : 4 và diện tích tam giác ABC là 150 cm2. Tính AM.
b) Biết tam giác ABC vuông tại A, AB = 15 cm, CM = 16 cm. Tính chu vi tam giác ABC.
Cho ∆ABC vuông tại A. Đường phân giác của góc A cắt cạnh BC tại D. Qua Đó kẻ đường thẳng vuông góc với BC cắt AC tại E a) CM ∆DEC đồng dạng với ∆ABC b) CM : DB= DE
Lời giải:
a. Xét tam giác $DEC$ và $ABC$ có:
$\widehat{C}$ chung
$\widehat{EDC}=\widehat{BAC}=90^0$
$\Rightarrow \triangle DEC\sim \triangle ABC$ (g.g)
b.
Từ tam giác đồng dạng phần a suy ra $\frac{DE}{DC}=\frac{AB}{AC}(1)$
Vì $AD$ là phân giác của góc $\widehat{A}$ nên:
$\frac{BD}{DC}=\frac{AB}{AC}(2)$
Từ $(1); (2)\Rightarrow \frac{DE}{DC}=\frac{BD}{DC}$
$\Rightarrow DE=BD$ (đpcm)
Cho tam giác abc vuông tại a phân giác góc abc tại d từ d vẽ đường thẳng vuông góc vs ac đg thẳng này cắt bc tại e a)cm dc.ab=da.cb b)cm cb/ab=ce/be
Cho tam giác ABC vuông tại A đường cao AH
a) AB=12cm,BC=20cm.Tính AC, AH, góc ABC(làm tròn đến độ)
B) kẻ HM vuông góc AB tại M, HN vuông góc AC tại N. CM: AN. NC=AC^2 -HC^2
c) CM: AH= MN, CM: AM. MB+AN. NC=AH^2
Tam giác ABC vuông tại A,tam giác DEF vuông tại D,cạnh AB=4 cm,cạnh BC=5 cm,DF=12 cm và EF=15 cm thì tam giác ABC đồng dạng với tam giác nào ?
Cho Tam giác ABC vuông tại a có ab 8 cm, ac = 7, bc= 10 cm chứng minh Tam giác abc vuông ?
Cho Tam giác ABC vuông tại a có ab 8 cm, ac = 7, bc= 10 cm chứng minh Tam giác abc vuông
Cho tam giác ABC vuông tại A có AB = 6 cm, AC= 8 cm, đường trung tuyến M. Gọi d là đường thẳng vuông góc với AM tại A. Kể BD vuông góc với d tại D, kẻ CE vuông góc với d tại E. a, Chứng minh: tam giác ABC đồng dạng với tam giác CAE. b, Tính CE
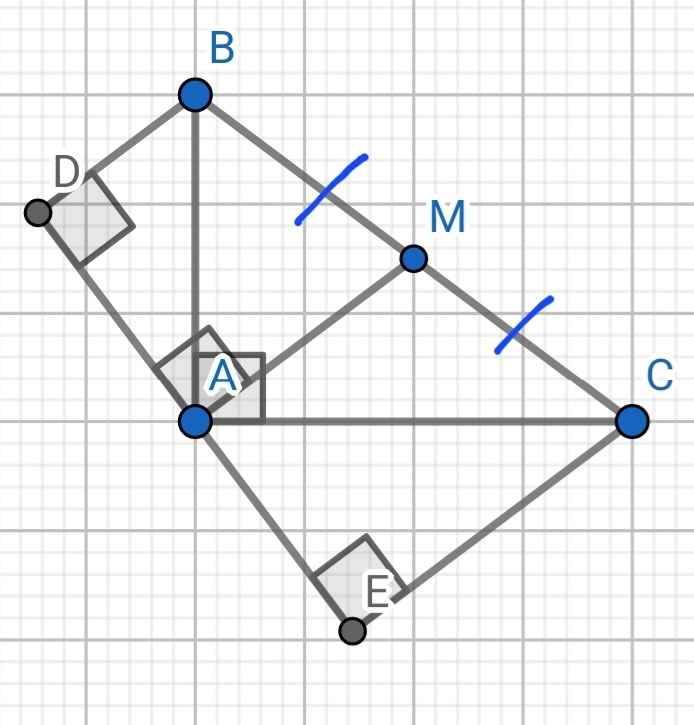
a) Sửa đề: Chứng minh ∆ABC ∽ ∆EAC
Giải:
∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do AM là đường trung tuyến ứng với cạnh huyền BC
⇒ AM = BM = CM = BC : 2
= 10 : 2 = 5 (cm)
∆AMC có AM = CM = 5 (cm)
⇒ ∆AMC cân tại M
⇒ ∠MAC = ∠MCA (hai góc ở đáy)
Do MA ⊥ DE (gt)
CE ⊥ DE (gt)
⇒ MA // DE
⇒ ∠MAC = ∠ACE (so le trong)
Mà ∠MAC = ∠MCA (cmt)
⇒ ∠MAC = ∠ACE
⇒ ∠ACE = ∠BCA (do ∠MAC = ∠BAC)
Xét hai tam giác vuông:
∆ABC và ∆EAC có:
∠BCA = ∠ACE (cmt)
⇒ ∆ABC ∽ ∆EAC (g-g)
b) Do ∆ABC ∽ ∆EAC (cmt)
⇒ AC/CE = BC/AC
⇒ CE = AC²/BC
= 8²/10
= 6,4 (cm)
1/ Cho tam giác ABC vuông tại A có đường phân giác AD và đường trung tuyến BM vuông góc tại E. Gọi H là trung điểm AE. BE cắt AC tại K.
a) Cm: tam giác BDK vuông cân tại D
b) Cm : (AD/AC)2 = 2/9
2/ Cho tam giác ABC vuông cân tại có đường trung tuyến AM. Vẽ MH vuông AB ( H thuộc AB ). Từ A hạ AI vuông CH tại I. Gọi N là giao điểm IC và AM. BI cắt AC tại K.
a) Cm: BI vuông với IM tại I
b) Cm: AN.AB = IC.MK