Question

Cho tam giác ABC vuông tại A có AB = 6 cm, AC= 8 cm, đường trung tuyến M. Gọi d là đường thẳng vuông góc với AM tại A. Kể BD vuông góc với d tại D, kẻ CE vuông góc với d tại E. a, Chứng minh: tam giác ABC đồng dạng với tam giác CAE. b, Tính CE

Answer 1

    

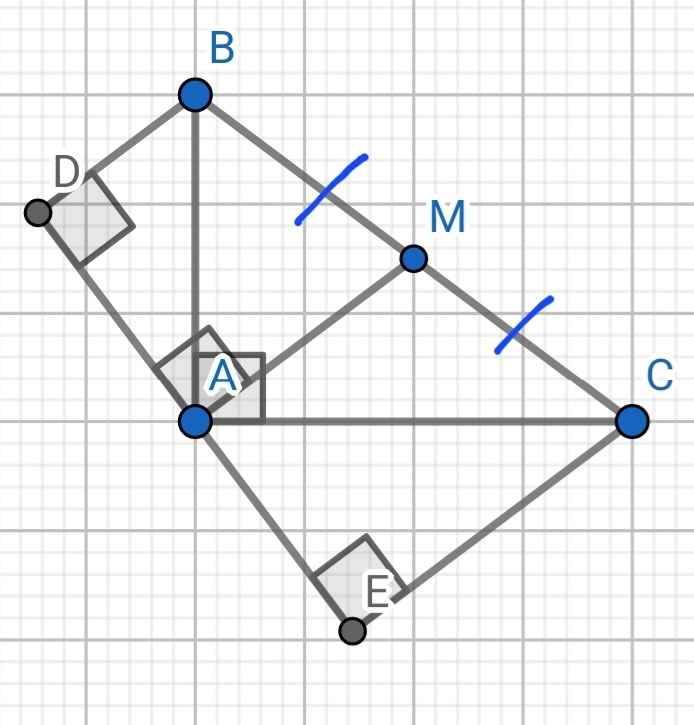
a) Sửa đề: Chứng minh ∆ABC ∽ ∆EAC

Giải:

∆ABC vuông tại A

⇒ BC² = AB² + AC² (Pytago)

= 6² + 8²

= 100

⇒ BC = 10 (cm)

Do AM là đường trung tuyến ứng với cạnh huyền BC

⇒ AM = BM = CM = BC : 2

= 10 : 2 = 5 (cm)

∆AMC có AM = CM = 5 (cm)

⇒ ∆AMC cân tại M

⇒ ∠MAC = ∠MCA (hai góc ở đáy)

Do MA ⊥ DE (gt)

CE ⊥ DE (gt)

⇒ MA // DE

⇒ ∠MAC = ∠ACE (so le trong)

Mà ∠MAC = ∠MCA (cmt)

⇒ ∠MAC = ∠ACE

⇒ ∠ACE = ∠BCA (do ∠MAC = ∠BAC)

Xét hai tam giác vuông:

∆ABC và ∆EAC có:

∠BCA = ∠ACE (cmt)

⇒ ∆ABC ∽ ∆EAC (g-g)

b) Do ∆ABC ∽ ∆EAC (cmt)

⇒ AC/CE = BC/AC

⇒ CE = AC²/BC

= 8²/10

= 6,4 (cm)

Answer 2