O2VÀ CD2 LÀ GÌ

Những câu hỏi liên quan
Hai góc ∠O2và ∠O4 (hình 1) có là hai góc đối đỉnh không ? Vì sao?
Ta có: Hai góc ∠O2và ∠O4là hai góc đối đỉnh vì mỗi cạnh góc ∠O1là tia đối của một cạnh ∠O4 và ngược lại
Đúng 0
Bình luận (0)
VIẾT CÁC phương trình hoá học xảy ra giữa các cặp chất sau :A)O2vàFe ;B)O2và AL
\(3Fe+2O_2\underrightarrow{^{t^0}}Fe_3O_4\)
\(4Al+3O_2\underrightarrow{^{t^0}}2Al_2O_3\)
Đúng 1
Bình luận (0)
Cho đtron tâm O đkinh AB. Gọi Hlaf trung điểm OA. Dây CD vuông với OA tại H.
a, Tứ giác ACOD là hình gì? Vì sao?
b, C/m các △OAC và CBD là △ đều
c, Gọi M là trung điểm BC. C/m 3 điểm D, O, M thẳng hàng
d, C/m: CD2 = 4AH.HB
a: ΔOCD cân tại O
mà OH là đường cao
nên H là trung điểm của CD
Xét tứ giác OCAD có
H là trung điểm chung của OA và CD
Do đó: OCAD là hình bình hành
Hình bình hành OCAD có OC=OD
nên OCAD là hình thoi
b: Xét ΔOAC có OC=CA=OA=R
nên ΔOAC đều
=>\(\widehat{CAO}=60^0\)
Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
=>\(\widehat{CAB}+\widehat{CBA}=90^0\)
=>\(\widehat{CBA}+60^0=90^0\)
=>\(\widehat{CBA}=30^0\)
Xét ΔBDC có
BH là đường cao
BH là đường trung tuyến
Do đó: ΔBDC cân tại B
ΔBDC cân tại B
mà BH là đường cao
nên BH là phân giác của góc CBD
=>\(\widehat{CBD}=2\cdot\widehat{CBH}=60^0\)
Xét ΔBCD cân tại B có \(\widehat{CBD}=60^0\)
nên ΔBCD đều
c: BO=OA
OA=2OH
Do đó: BO=2OH
=>BO/BH=2/3
Xét ΔCDB có
BH là đường trung tuyến
\(BO=\dfrac{2}{3}BH\)
Do đó: O là trọng tâm của ΔCDB
Xét ΔCDB có
O là trọng tâm
M là trung điểm của BC
Do đó: D,O,M thẳng hàng
d: Xét ΔCAB vuông tại C có CH là đường cao
nên \(AH\cdot HB=CH^2\)
=>\(4\cdot AH\cdot HB=4\cdot CH^2=\left(2CH\right)^2=CD^2\)
Đúng 1
Bình luận (0)
Nhận biết, phân biệt các hợp chất hữu cơ.
a. CH4, CO2, C2H4, C2H2
b. CH4, C2H2, O2và CO2
c. C2H2, CH4, C2H4, SO2, CO2
a, - Dẫn từng khí qua Ca(OH)2 dư.
+ Có tủa trắng: CO2
PT: \(CO_2+Ca\left(OH\right)_2\rightarrow CaCO_3+H_2O\)
+ Không hiện tượng: CH4, C2H4, C2H2. (1)
- Dẫn khí nhóm (1) qua dd AgNO3/NH3.
+ Xuất hiện tủa vàng: C2H2.
PT: \(C_2H_2+2AgNO_3+2NH_3\rightarrow Ag_2C_2+2NH_4NO_3\)
+ Không hiện tượng: CH4, C2H4. (2)
- Dẫn khí nhóm (2) qua dd brom dư.
+ Dd nhạt màu dần: C2H4.
PT: \(C_2H_4+Br_2\rightarrow C_2H_4Br_2\)
+ Không hiện tượng: CH4.
b, - Dẫn từng khí qua dd Ca(OH)2
+ Xuất hiện tủa trắng: CO2
PT: \(CO_2+Ca\left(OH\right)_2\rightarrow CaCO_3+H_2O\)
+ Không hiện tượng: CH4, C2H2 và O2. (1)
- Dẫn khí nhóm (1) qua dd AgNO3/NH3.
+ Có tủa vàng: C2H2.
PT: \(C_2H_2+2AgNO_3+2NH_3\rightarrow Ag_2C_2+2NH_4NO_3\)
+ Không hiện tượng: CH4 và O2. (2)
- Cho tàn đóm đỏ vào 2 khí nhóm (2)
+ Que đóm bùng cháy: O2.
+ Không hiện tượng: CH4.
c, - Dẫn từng khí qua dd Ca(OH)2.
+ Có tủa trắng: SO2, CO2 (1)
PT: \(SO_2+Ca\left(OH\right)_2\rightarrow CaSO_3+H_2O\)
\(CO_2+Ca\left(OH\right)_2\rightarrow CaCO_3+H_2O\)
+ Không hiện tượng: C2H2, CH4 và C2H4. (2)
- Dẫn khí nhóm (1) qua dd nước brom dư.
+ Dd nhạt màu dần: SO2
PT: \(SO_2+Br_2+2H_2O\rightarrow2HBr+H_2SO_4\)
+ Không hiện tượng: CO2.
- Dẫn khí nhóm (2) qua dd AgNO3/NH3
+ Có tủa vàng: C2H2.
PT: \(C_2H_2+2AgNO_3+2NH_3\rightarrow Ag_2C_2+2NH_4NO_3\)
+ Không hiện tượng: CH4, C2H4 (3)
- Dẫn khí nhóm (3) qua dd brom dư.
+ Dd nhạt màu dần: C2H4
PT: \(C_2H_4+Br_2\rightarrow C_2H_4Br_2\)
+ Không hiện tượng: CH4.
Đúng 2
Bình luận (0)
Cho đường tròn tâm O đường kính AB. Gọi H là trung điểm OA. Dây CD vuông góc với OA tại H.
1. Tứ giác ACOD là hình gì? Tại sao?
2. Chứng minh các tam giác OAC và CBD là các tam giác đều.
3. Gọi M là trung điểm BC. Chứng minh ba điểm D,O, M thẳng hàng.
4. Chứng minh đẳng thức CD2 = 4 AH. HB
Cho đường tròn tâm O đường kính AB. Gọi H là trung điểm OA. Dây CD vuông góc với OA tại H.
1. Tứ giác ACOD là hình gì? Tại sao?
2. Chứng minh các tam giác OAC và CBD là các tam giác đều.
3. Gọi M là trung điểm BC. Chứng minh ba điểm D,O, M thẳng hàng.
4. Chứng minh đẳng thức CD2 = 4 AH. HB
a, xét tam giác CHA và tg CHO có : CH chung
AH = HO do H là trđ của AO (gt)
^CHA = ^CHO = 90
=> tg CHA = tg CHO (2cgv)
=> CH = CO
có AB _|_ CD => A là điểm chính giữa của cung CD => AC = AD mà OC = OD
=> AC = CO = OD = DA
=> ACOD là hình thoi
b, C thuộc đường tròn đường kính AB => ^ACB = 90 => AC _|_ CB
có AC // DO do ACOD là hình thoi
=> DO _|_ CB
M là trung điểm của dây BC (Gt) => OM _|_ BC (định lí)
=> D;O;M thẳng hàng
c, xét tg ACB có ^ACB = 90 và CH _|_ AB
=> AH.HB = CH^2
=> 4AH.HB = 4CH^2
=> 4AH.HB = (2CH)^2
mà 2CH = CD
=> CD^2 = 4AH.HB
Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung đếm của AD, BC, AC. Chứng minh rằng: E F ≤ A B + C D 2
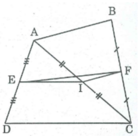
Với 3 điểm E,I,F bất kì ta có: EF ≤ EI + IF (dấu “ = ” xảy ra khi I nằm giữa E và F) mà EI = CD / 2 ; IF= AB / 2 (chứng minh trên)
⇒ E F ≤ C D 2 + A B 2
Vậy E F ≤ A B + C D 2 (dấu bằng xảy ra khi AB // CD)
Đúng 0
Bình luận (0)
Viết cân bằng tạo phức khi thêm dần dung dịch KCN vào dung dịch
Cd(NO3)2, biết Cd2+ tạo phức với CNcó số phối trí cực đại là 4.
Viết cân bằng tạo phức khi thêm dần dung dịch KCN vào dung dịch Cd(NO3)2, biết Cd2+ tạo phức với CN- có số phối trí cực đại là 4.
\(KCN->K^++CN^-\\ Cd\left(NO_3\right)_2->Cd^{2+}+2NO_3^-\\ Cd^{2+}+CN^-⇌\left[Cd\left(CN\right)\right]^+\\ \left[Cd\left(CN\right)\right]^++CN^-⇌\left[Cd\left(CN\right)_2\right]\\ \left[Cd\left(CN\right)_2\right]+CN^-⇌\left[Cd\left(CN\right)_3\right]^-\\ \left[Cd\left(CN\right)_3\right]^-+CN^-⇌\left[Cd\left(CN\right)_4\right]^{2-}\)
Đúng 3
Bình luận (0)
Cho hình bình hành ABCD. CM: AB2 + BC2 + CD2 +DA2 = AC2 +BD2
Ta có: \(AC^2+BD^2=\left(\overrightarrow{AB}+\overrightarrow{AD}\right)^2+\left(\overrightarrow{BC}+\overrightarrow{BA}\right)^2\)
\(=AB^2+AD^2+2\overrightarrow{AB}.\overrightarrow{AD}+BC^2+BA^2+2\overrightarrow{BA}.\overrightarrow{BC}\)
\(=AB^2+AD^2+BC^2+AD^2+2\overrightarrow{AB}\left(\overrightarrow{AD}-\overrightarrow{BC}\right)\)
\(=AB^2+AD^2+BC^2+AD^2\)
Đúng 0
Bình luận (0)





















