Cho góc xOy trên tia phân giác của góc đó lấy điểm M, từ M hạ các đường vuông góc với MA, MB xuống các cạnh Ox, Oy. Chứng minh AB vuông góc với OM
Những câu hỏi liên quan
Cho góc xOy khác góc bẹt. Trên tia phân giác của góc đó lấy điểm M. Từ M hạ các đường vuông góc MA, MB xuống các cạnh Ox, Oy. c/m:
Tam giác MAB cân
AB vuông góc với OM
a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔOAM=ΔOBM
Suy ra: MA=MB
hayΔMBA cân tại M
b: Ta có: ΔOAM=ΔOBM
nên OA=OB
=>ΔOAB cân tại O
mà OM là đường phân giác
nên OM là đường cao
Đúng 0
Bình luận (0)
Cho góc xOy khác góc bẹt.a) Từ điểm M trên tia phân giác của góc xOy, kẻ các đường vuông góc MA, MB đến hai cạnh Ox, Oy (A thuộc Ox, B thuộc Oy), OM cắt AB tại H. Chứng minh
A
B
⊥
O
M
.
b) Trên tia đối của tia Ox, Oy lần lượt lấy hai điểm C và D, sao cho OC OD. Hai đương thẳng lần lượt vuông góc với Ox, Oy tại C và D cắt nhau ở E. Chứng minh ba điểm O, H, E thẳng hàng.
Đọc tiếp
Cho góc xOy khác góc bẹt.
a) Từ điểm M trên tia phân giác của góc xOy, kẻ các đường vuông góc MA, MB đến hai cạnh Ox, Oy (A thuộc Ox, B thuộc Oy), OM cắt AB tại H. Chứng minh A B ⊥ O M .
b) Trên tia đối của tia Ox, Oy lần lượt lấy hai điểm C và D, sao cho OC = OD. Hai đương thẳng lần lượt vuông góc với Ox, Oy tại C và D cắt nhau ở E. Chứng minh ba điểm O, H, E thẳng hàng.
Cho Oz là tia phân giác của góc xOy. Lấy điểm M trên tia Oz và hai điểm A, B lần lượt trên các tia Ox, Oy sao cho MA vuông góc với Ox, MB vuông góc với Oy(H.4.50). Chứng minh rằng MA = MB.
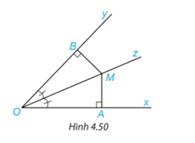
Xét hai tam giác vuông OBM và OAM có:
OM chung
\(\widehat {BOM} = \widehat {AOM}\) (gt)
\( \Rightarrow \Delta OBM = \Delta OAM\)(cạnh huyền – góc nhọn)
Suy ra MB=MA ( 2 cạnh tương ứng)
Đúng 1
Bình luận (0)
Cho xOy ̂ , trên tia phân giác của góc đó lấy một điểm M, kẻ MA, MB vuông góc lần lượt với Ox, Oy. Chứng minh rằng: a) ΔMAB cân; b) AB ⊥ OM.
Cho góc xOy, Ot là tia phân giác của góc xOy. Trên tia Ot lấy điểm M, kẻ MA vuông góc với Ox, MB vuông góc với Oy. Chứng minh rằng:
a) OA=OB
b) MO là tia phân giác của góc AMB
c) OM vuông góc với AB
a) Xét tam giác vuông AMO và tam giác vuông BMO :
góc MOA = góc MOB (gt)
OM là cạnh chung
=>tam giác vuông AMO = tam giác vuông BMO (cạnh huyền + góc nhọn)
=> OA=OB ( 2 cạnh tương ứng)
b) theo a) ta có : tam giác AMO = tam giác BMO
=>góc AMO = góc BMO
=> MO là tia phân giác của góc AMB
c) gọi C là giao điểm của OM và AB
Xét tam giác OAC và tam giác OBC có:
góc AOC = góc BOC (gt)
OC là cạnh chung
OA = OB (theo a)
=>tam giác OAC = tam giác OBC
=> góc ACO = góc BCO
mà hai góc này kề bù
=> góc ACO = góc BCO = 90 độ
=> OM vuông góc với AB
Đúng 0
Bình luận (0)
Bài 4: Cho góc nhọn xOy, phân giác Ot. lấy M trong góc xOy. Từ M hạ MA vuông góc với Ox, MB vuông góc với Oy. Góc C là giao điểm của MA và Ot. Từ C hạ CD vuông góc với Oy.
a, So Sánh MB và MD
b,Chứng minh MB < MA
Cho x góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA=OB. Từ A hạ AC vuông góc với Oy, từ B hạ BD vuông góc với Ox( C nằm trên Oy, B nằm trên Ox)
a) Chứng minh OC=OD
b) Chứng minh AB // CD
c) I là giao điểm của các đoạn thẳng ÁC và BD. Chứng minh OI là đường phân giác của góc xOy và cũng là đường phân giác của góc COD
Cho góc nhọn xOy gọi Ot là tia phân giác của góc xOy, lấy điểm M thuộc Ot. Kẻ MA vuông góc với Ox tại A, kẻ MB vuông góc với Oy tại B
Chứng minh MA = MB
Đường thẳng BM cắt Ox tại D và đường thẳng AM cắt Oy tại E
Chứng minh MD = ME
Chứng minh OM vuông góc với DE
vẽ góc xOy, Oz là tia phân giác của góc xOy, lấy điểm M bất kì thuộc Oz. Từ M kẻ MA vuông góc với Ox,MB vuông góc với Oy. Chứng minh MA=MB
Vì Oz là tia phân giác của góc xOy
=>góc AOM = góc BOM
VÌ MA\(\perp\)Ox =>góc MAO=90o
MB \(\perp\)Oy =>góc MBO=90o
Xét \(\Delta AOM\)và \(\Delta BOM\)có:
Góc MAO= Góc MBO(Cùng bằng 90o)
OM:cạnh chung
Góc AOM = góc BOM
=>\(\Delta AOM=\Delta BOM\left(Ch-gn\right)\)
=>MA=MB(các cạnh tương ứng)
Đúng 1
Bình luận (0)
Cho góc xOy. Lấy điểm A trên tia Ox, điểm B trên tia Oy. Vẽ các tia phân giác của các góc BAx và ABy cắt nhau tại M.
A) Chứng minh OM là tia phần giác góc xOy.
b) Từ M vẽ một đường thẳng vuông góc với OM, cắt Ox, Oy lần lượt tại C và D. Chứng minh rằng tam giác OCD cân.
LÀM ƠN PLEASE !!! MIK CẦN GẤP