Xét hai tam giác vuông OBM và OAM có:
OM chung
\(\widehat {BOM} = \widehat {AOM}\) (gt)
\( \Rightarrow \Delta OBM = \Delta OAM\)(cạnh huyền – góc nhọn)
Suy ra MB=MA ( 2 cạnh tương ứng)
Vẽ tam giác vuông ABC có A = 90°, AB = 3 cm, BC = 5 cm theo các bước sau:
• Dùng thước thẳng có vạch chia vẽ đoạn thẳng AB = 3 cm.
• Vẽ tia Ax vuông góc với AB và cung tròn tâm B bán kính 5 cm như Hình 4.51.
Cung tròn cắt tia Ax tại điểm C.
•Vẽ đoạn thẳng BC ta được tam giác ABC.
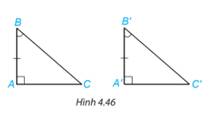
Hai tam giác vuông ABC (vuông tại đỉnh A) và ABC vuông tại đỉnh A) có tương ứng một cạnh góc vuông và một góc nhọn kề với cạnh ấy bằng nhau: AB = A'B', \(\widehat B = \widehat {B'}\) (H.4.46).
Dựa vào trường hợp bằng nhau góc cạnh - góc của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
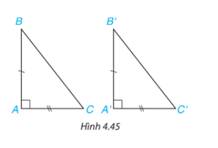
Hai tam giác vuông ABC (vuông tại đỉnh A) và A’B’C’ (vuông tại đỉnh A’) có các cặp cạnh góc vuông bằng nhau: AB = A'B', AC = A'C' (H.4.45). Dựa vào trường hợp bằng nhau cạnh - góc - cạnh của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
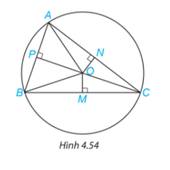
Cho ba điểm A, B, C nằm trên đường tròn tâm O và các điểm M, N, P như Hình 4.54. Hãy chỉ ra ba cặp tam giác vuông bằng nhau trong hình.
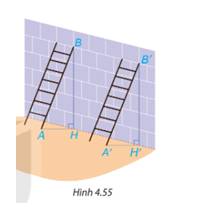
Có hai chiếc thang dài như nhau được dựa vào một bức tường với cùng độ cao BH = B’H’ như Hình 4.55. Các góc BAH và B'A'H có bằng nhau không? Vì sao?
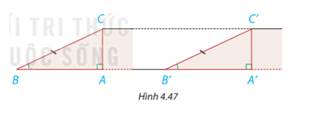
Hình 4.47 mô phỏng chiều dài và độ dốc của hai con dốc bởi các đường thẳng BC, B’C’ và các góc B, B’. Khi đó AC, A’C’ mô tả độ cao của hai con dốc.
Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC.
Chứng minh rằng \(\Delta ABM = \Delta DCM\).
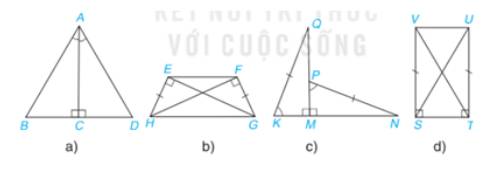
Trong Hình 4.48, hãy tìm các cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.
Mỗi hình sau có các cặp tam giác vuông nào bằng nhau? Vì sao?
