Ở bài 24, tại sao công delta A'= -delta A mà lại có thể thắng được công delta A?

Những câu hỏi liên quan
Quan sát Hình 8, cho biết \(DC//MP,EF//MQ\).
a) Chứng minh rằng \(\Delta EPF\backsim\Delta DCQ\).
b) \(\Delta ICF\) có đồng dạng với \(\Delta MPQ\)không? Tại sao?
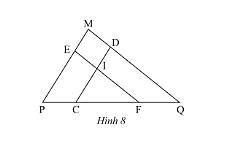
a) Xét tam giác \(MPQ\)có \(EF//MQ\) nên \(\Delta MPQ\backsim\Delta EPF\) (định lí) (1)
Xét tam giác \(MPQ\)có \(DC//MP\) nên \(\Delta MPQ\backsim\Delta DCQ\) (định lí) (2)
Từ (1) và (2) \(\Delta EPF\backsim\Delta DCQ\) (tính chất tam giác đồng dạng)
b) Xét tam giác \(EPF\)có \(IC//EP\) nên \(\Delta ICF\backsim\Delta EPF\) (định lí) (3)
Từ (1) và (3) suy ra, \(\Delta ICF\backsim\Delta MPQ\).
Đúng 0
Bình luận (0)
Cho Delta ABC có widehat{A} 90 độ, vẽ tia phân giác widehat{C} cắt AB ở H. Lấy E inBC sao cho CA CEa) Chứng minh DeltaCAH DeltaCEH và HE perp BCb) Kẻ EK perp AC tại K, EK cắt CH tại I. Chứng minh widehat{HEI}-widehat{HAI}c) Chứng minh HE // AI và widehat{AIE}-widehat{ABC} 90 độ
Đọc tiếp
Cho \(\Delta ABC\) có \(\widehat{A}\)= 90 độ, vẽ tia phân giác \(\widehat{C}\) cắt AB ở H. Lấy E \(\in\)BC sao cho CA = CE
a) Chứng minh \(\Delta\)CAH = \(\Delta\)CEH và HE \(\perp\) BC
b) Kẻ EK \(\perp\) AC tại K, EK cắt CH tại I. Chứng minh \(\widehat{HEI}-\widehat{HAI}\)
c) Chứng minh HE // AI và \(\widehat{AIE}-\widehat{ABC}\)= 90 độ
Cho ΔABC vuông tại A trên cạnh BC lấy điểm F sao cho BF = BA. Qua F kẻ đường thẳng vuông góc với BC cắt A tại D.
a/ C/m:ΔABD =ΔFBD.
b/ FD cắt BA tại E. Chứng minh ΔABC =ΔFBE.
Xem chi tiết
a) Xét ΔABD vuông tại A và ΔFBD vuông tại F có
BD là cạnh chung
BA=BF(gt)
Do đó: ΔABD=ΔFBD(cạnh huyền-cạnh góc vuông)
b) Xét ΔAED vuông tại A và ΔFCD vuông tại F có
DA=DF(ΔABD=ΔFBD)
\(\widehat{ADE}=\widehat{FDC}\)(hai góc đối đỉnh)
Do đó: ΔAED=ΔFCD(cạnh góc vuông-góc nhọn kề)
⇒AE=FC(hai cạnh tương ứng)
Ta có: AE+AB=EB(A nằm giữa E và B)
FC+FB=BC(F nằm giữa B và C)
mà AE=FC(cmt)
và AB=FB(gt)
nên EB=BC
Xét ΔABC vuông tại A và ΔFEB vuông tại F có
BC=EB(cmt)
BA=BF(gt)
Do đó: ΔABC=ΔFEB(cạnh huyền-cạnh góc vuông)
Đúng 0
Bình luận (0)
Bài 1:Cho góc nhọn xOy.Trên tia Ox lấy điểm A,trên tia Oy lấy điểm B sao cho OAOB.Trên tia Ax lấy điểm C,trên tia By lấy điểm D sao cho ACBDa) Chứng minh:ADBCb) Gọi E là giao điểm AD và Bc.Chứng minh:Delta EACDelta EBDc) Chứng minh:OE là phân giác của góc xOyBài 2:Cho Delta ABCcó widehat{A}90^o.Kẻ AH vuông góc với BC left(Hvarepsilon BCright).Trên đường thẳng vuông góc với BC tại B lấy điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho BDAHChứng minh rằng:a) Delta AHBDelta DBHb) AB//DHc)...
Đọc tiếp
Bài 1:
Cho góc nhọn xOy.Trên tia Ox lấy điểm A,trên tia Oy lấy điểm B sao cho OA=OB.Trên tia Ax lấy điểm C,trên tia By lấy điểm D sao cho AC=BD
a) Chứng minh:AD=BC
b) Gọi E là giao điểm AD và Bc.Chứng minh:\(\Delta EAC=\Delta EBD\)
c) Chứng minh:OE là phân giác của góc xOy
Bài 2:
Cho \(\Delta ABC\)có \(\widehat{A}=90^o\).Kẻ AH vuông góc với BC \(\left(H\varepsilon BC\right)\).Trên đường thẳng vuông góc với BC tại B lấy điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho BD=AH
Chứng minh rằng:
a) \(\Delta AHB=\Delta DBH\)
b) AB//DH
c) Tính \(\widehat{ACB}\),biết \(\widehat{BAH=35^o}\)
Bài 3:
Cho \(\overline{\Delta}ABC\) vuông tại A có \(\overline{\Delta}B=30^o\)
a) Tính \(\Delta C\)
b) Vẽ tia phân giác của góc C cắt cạnh AB tại D
c) Trên cạnh CB lấy điểm M sao cho CM=CA.Chứng minh \(\Delta ACD=\Delta MCD\)
d) Qua C vẽ đường thẳng xy vuông góc CA.Từ A kẻ đường thẳng song song với CD cắt xy ở K.Chứng minh:AK=CD
e) Tính \(\DeltaẠKC\)
Bài 4:
Cho tam giác ABC vuông tại A,có AB=AC.Gọi K là trung điểm của cạnh BC
a) Chứng minh \(\Delta AKB=\Delta AKC\)và \(AK⊥BC\)
b) Từ C kẻ đường vuông góc với BC,nó cắt AB tại E.Chứng minh EC//AK
c) Chứng minh CE=CB
Nhờ cao nhân giải đáp, mình cảm ơn nhiều nhé 1) Tại sao t0 vật lại ở biên trên ( do ta giả định Adelta L phải không nhỉ? )2) Khi tác dụng lực F- sao ta biết được vật dịch 4 cm đến đúng vị trí biên mà con lắc lại còn đứng yên trùng với vtcb luôn nữa chứ?
Đọc tiếp
Nhờ cao nhân giải đáp, mình cảm ơn nhiều nhé ![]()
1) Tại sao t=0 vật lại ở biên trên ( do ta giả định A=delta L phải không nhỉ? )
2) Khi tác dụng lực F- sao ta biết được vật dịch 4 cm đến đúng vị trí biên mà con lắc lại còn đứng yên trùng với vtcb luôn nữa chứ?
Cho hai đường thẳng {Delta _1},{Delta _2}cắt nhau tại I và có vectơ chỉ phương lần lượt là overrightarrow {{u_1}} ,overrightarrow {{u_2}} . Gọi A và B là các điểm lần lượt thuộc hai đường thẳng {Delta _1} và {Delta _2} sao cho overrightarrow {{u_1}} overrightarrow {IA} ,overrightarrow {{u_2}} overrightarrow {IB} .a) Quan sát Hình 41a, Hình 41b, hãy nhận xét về độ lớn của góc giữa hai đường thẳng{Delta _1},{Delta _2}và độ lớn của góc giữa hai vectơ overrightarrow {IA} ,overrightarrow {IB} b)...
Đọc tiếp
Cho hai đường thẳng \({\Delta _1},{\Delta _2}\)cắt nhau tại I và có vectơ chỉ phương lần lượt là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \). Gọi A và B là các điểm lần lượt thuộc hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) sao cho \(\overrightarrow {{u_1}} = \overrightarrow {IA} ,\overrightarrow {{u_2}} = \overrightarrow {IB} \).
a) Quan sát Hình 41a, Hình 41b, hãy nhận xét về độ lớn của góc giữa hai đường thẳng
\({\Delta _1},{\Delta _2}\)và độ lớn của góc giữa hai vectơ \(\overrightarrow {IA} \),\(\overrightarrow {IB} \)
b) Chứng tỏ cos(\({\Delta _1},{\Delta _2}\)) = \(\left| {cos\left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)} \right|\).
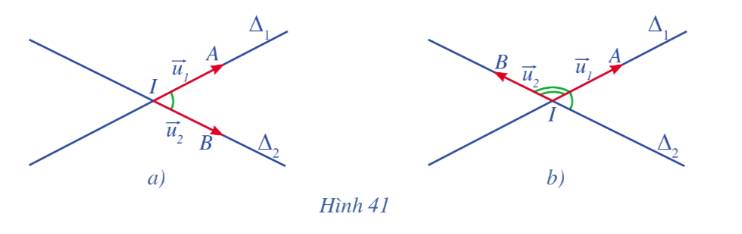
a) Độ lớn của góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) và độ lớn của góc giữa hai vectơ \(\overrightarrow {IA} \),\(\overrightarrow {IB} \)có thể bẳng nhau hoặc bù nhau.
b) Nếu \(\left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) \le {90^o}\)thì \(\left( {{\Delta _1},{\Delta _2}} \right) = \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\). Do đó,\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\) và \(\cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) \ge 0\).
Nếu \(\left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) > {90^o}\)thì \(\left( {{\Delta _1},{\Delta _2}} \right) = {180^o} - \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\). Do đó,\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = - \cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\) và \(\cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) < 0\).
Vậy ta có: \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)} \right|\)
Đúng 0
Bình luận (0)
Bài 1 Cho tam giá ABC vuông tại A. M là trung điểm AC. Trên tia đối của tia MB lấy điểm D sao cho MDMB. Chứng minh: a) Delta ABCDelta CMD b) Góc ACD 90o và AB // CDBài 2: Một tam giác có ba cạnh tỉ lệ với 2;3;5 và có chu vi là 50cm. Tính các cạnh của tam giá đó.Bài 3: Cho tam giác ABC vuông tại A. Đường phân giác của góc B cắt AC tại E. Kẻ EH vuông góc với BC tại H. Gọi K là giao điểm của AB và HE. Chứng minh rằng: a) Delta ABEDelta HBE b) Delta AEKDelta HECvà EK EC
Đọc tiếp
Bài 1 Cho tam giá ABC vuông tại A. M là trung điểm AC. Trên tia đối của tia MB lấy điểm D sao cho MD=MB. Chứng minh:
a) \(\Delta ABC=\Delta CMD\)
b) Góc ACD = 90o và AB // CD
Bài 2: Một tam giác có ba cạnh tỉ lệ với 2;3;5 và có chu vi là 50cm. Tính các cạnh của tam giá đó.
Bài 3: Cho tam giác ABC vuông tại A. Đường phân giác của góc B cắt AC tại E. Kẻ EH vuông góc với BC tại H. Gọi K là giao điểm của AB và HE. Chứng minh rằng:
a) \(\Delta ABE=\Delta HBE\)
b) \(\Delta AEK=\Delta HEC\)và EK = EC
Cho ΔABC vuông tại A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC.
C/m: a, ΔABC = ΔABD
b, Trên tia AD lấy điểm M. Chứng minh ΔMBD = ΔMBC
a) Xét tam giác ABC và tam giác ABD cùng vuông tại A, ta có :
BA là cạnh chung
DA=AC ( Giả thiết )
=> Tam giác ABC = Tam giác ABD ( Cạnh vuông-cạnh vuông )
b) Xem lại đề.
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A ( AB < AC ), đường cao AH ( H ϵ BC ). Trên đoạn thẳng HC lấy điểm D sao cho HD=HA. Đường thẳng vuông góc với BC tại D cắt AC ở E. Gọi M là trọng điểm của đoạn thằng BE, CM.
a/ ΔDEC ∞ ΔABC
b/ ΔADC ∞ ΔBEC
c/ AB . AC = BC . AH
d/ ∠AHM= 45 độ
a: Xét ΔDEC vuông tạiD và ΔABC vuông tại A có
góc C chung
Do đó: ΔDEC\(\sim\)ΔABC
Suy ra: CD/CA=CE/CB
hay CD/CE=CA/CB
b: Xét ΔADC và ΔBEC có
CA/CB=CD/CE
góc DCA chung
Do đo: ΔADC\(\sim\)ΔBEC
c: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{AH\cdot BC}{2}\)
nên \(AB\cdot AC=AH\cdot BC\)
Đúng 0
Bình luận (0)












