
tìm khoảng ĐB, NB
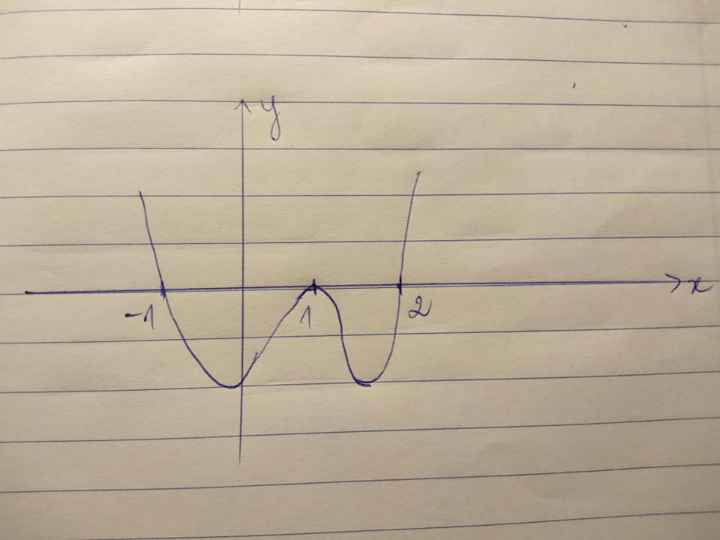
Cho hàm số y=f(x) liên tục trên R có đồ thị y=f '(x) như hình vẽ:
a)Tìm min, max của hàm số g(x)=f(\(\sqrt{8-x^2-2x}-1\))
b)Xác định khoảng đb, nb, cực đại, cực tiểu của g(x)=f(x2+x)
a.
TXĐ: \(D=\left[-4;2\right]\)
\(0\le\sqrt{9-\left(x+1\right)^2}\le3\Rightarrow-1\le\sqrt{9-\left(x+1\right)^2}\le2\)
\(\Rightarrow f'\left(\sqrt{8-x^2-2x}-1\right)\le0\) ; \(\forall x\in D\)
\(g'\left(x\right)=-\dfrac{x+1}{\sqrt{8-x^2-2x}}.f'\left(\sqrt{8-x^2-2x}-1\right)\) luôn cùng dấu \(x+1\)
\(\Rightarrow g\left(x\right)\) đồng biến trên \(\left[-1;2\right]\) và nghịch biến trên \(\left[-4;-1\right]\)
Từ BBT ta thấy \(g\left(x\right)_{max}=g\left(-4\right)=g\left(2\right)=f\left(-1\right)=?\)
\(g\left(x\right)_{min}=g\left(-1\right)=f\left(2\right)=?\)
(Do đề chỉ có thế này nên ko thể xác định cụ thể được min-max)
b.
\(g'\left(x\right)=\left(2x+1\right).f'\left(x^2+x\right)=0\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\f'\left(x^2+x\right)=0\left(1\right)\end{matrix}\right.\)
Xét (1), ta chỉ cần quan tâm 2 nghiệm bội lẻ:
\(f'\left(x^2+x\right)=0\Rightarrow\left[{}\begin{matrix}x^2+x=-1\left(vô-nghiệm\right)\\x^2+x=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Với \(\left[{}\begin{matrix}x\le-2\\x\ge1\end{matrix}\right.\) \(\Rightarrow x^2+x\ge2\) ; với \(-2\le x\le1\Rightarrow-1\le x^2+x\le2\) nên ta có bảng xét dấu:

Từ BBT ta có: \(x=-\dfrac{1}{2}\) là cực đại, \(x=-2;x=1\) là 2 cực tiểu
Hàm đồng biến trên ... bạn tự kết luận
Chứng minh: Hàm số y=f(x) =ax3(a khác 0) ĐB trên R khi a>0 và NB trên R khi a<0
Khi a>0 thì y>0
=> Hàm số đồng biến khi a>0
Khi a<0 thì y>0
=> Hàm só nghịch biến khi a<0
Lời giải:
Lấy $x_1\neq x_2\in\mathbb{R}$. Để hàm số đồng biến thì:
$\frac{y(x_1)-y(x_2)}{x_1-x_2}>0$
$\Leftrightarrow \frac{(3m-6)(x_1^2-x_2)^2}{x_1-x_2}=(3m-6)(x_1+x_2)>0$
Khi $x>0$ thì $x_1+x_2>0$. Để $y$ đồng biến khi $x>0$ thì $3m-6>0\Leftrightarrow m>2$
Khi $x<0$ thì $x_1+x_2< 0$. Để $y$ đồng biến khi $x< 0$ thì $3m-6< 0\Leftrightarrow m< 2$
Cho hàm số \(y=-\left(m^2+5m\right)x^3+6mx^2+6x-5\)
XĐ m để hs đơn điệu trên R. Khi đó, hs ĐB hay NB? Tại sao?
Tìm vị trí M, N để tổng khoảng cách: AM + MN + NB nhỏ nhất?
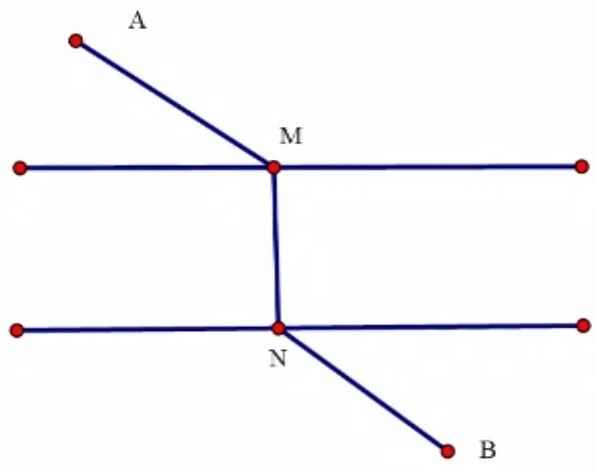
Vì MN cố định nên cần chứng minh AM+NB nhỏ nhất hay AM và NB nhỏ nhất
AM và NB nhỏ nhất \(\Leftrightarrow\) AM và BN lần lượt là hình chiếu của A,B lên các đường thẳng tương ứng
\(\Leftrightarrow\) M và N là chân đường vuông góc từ A,B đến các đường thẳng tương ứng
Vậy \(AM+MN+NB\) nhỏ nhất \(\Leftrightarrow\) M và N là chân đường vuông góc từ A,B đến các đường thẳng tương ứng
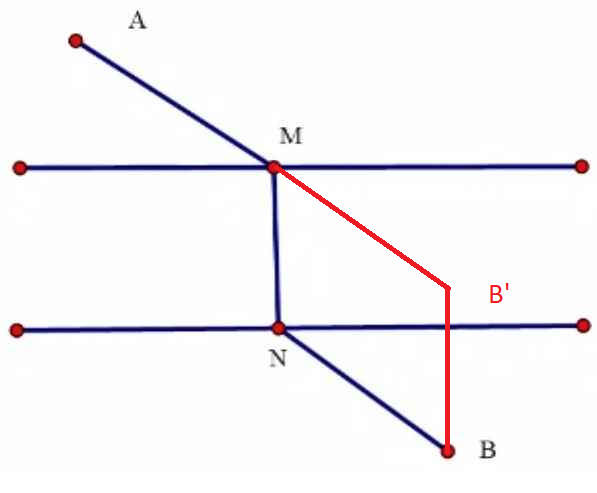 AM+MN+NB nhỏ nhất, MN cố định <=> AM+NB nhỏ nhất.
AM+MN+NB nhỏ nhất, MN cố định <=> AM+NB nhỏ nhất.
Gọi T\(\overrightarrow{NM}\)(B) = B'
Có NB=MB' <=> AM + MB' nhỏ nhất <=> A,M,B' thẳng hàng
=> M là giao điểm AB' với d1
=> N là hình chiếu vuông góc của M xuống d2
Sắp xếp các đồng bằng duyên hải miền Trung theo thứ tự từ Nam ra Bắc
A) ĐB Ninh Thuận- Bình Thuận; ĐB Bình Phú – Khánh Hòa ; ĐB Nam Ngãi ; ĐB Bình –Trị – Thiên ; ĐB Thanh – Nghệ – Tĩnh.
B) ĐB Thanh – Nghệ – Tĩnh; ĐB Bình –Trị – Thiên ; ĐB Nam Ngãi; ĐB Bình Phú – Khánh Hòa; ĐB Ninh Thuận- Bình Thuận.
C) ĐB Ninh Thuận- Bình Thuận ; ĐB Nam Ngãi; ĐB Bình Phú – Khánh Hòa ; ĐB Bình –Trị – Thiên ; ĐB Thanh – Nghệ – Tĩnh
ĐB: đồng bằng
Các đồng bằng duyên hải miền Trung sắp xếp theo thứ tự từ Nam ra Bắc là: A. ĐB Ninh Thuận - Bình Thuận; ĐB Bình Phú - Khánh Hòa; ĐB Nam Ngãi; ĐB Bình -Trị - Thiên; ĐB Thanh - Nghệ - Tĩnh. B. ĐB Thanh - Nghệ - Tĩnh; ĐB Bình - Trị - Thiên; ĐB Nam Ngãi; ĐB Bình Phú - Khánh Hòa; ĐB Ninh Thuận - Bình Thuận. C. ĐB Ninh Thuận - Bình Thuận; ĐB Nam Ngãi; ĐB Bình Phú - Khánh Hòa; ĐB Bình - Trị - Thiên; ĐB Thanh - Nghệ - Tĩnh. Câu 3: (2 điểm) Tính nhanh: a. 399×45+55×399 1995×1996−1991×1995 b.
CMR các hàm số Đb , NB
1, y= \(sin^2x\)+x
2 ,y= \(3sinx-4sin^3x+3x\)3
3, y= \(cos^2x+x^3+3x^2+4x-2\)
a/ \(y'=2sinx.cosx+1=\left(sinx+cosx\right)^2\ge0\) ;\(\forall x\)
\(\Rightarrow\) Hàm đồng biến trên R
b/ Số cuối là 3x hay \(3x^3\) vậy nhỉ?
c/ \(y'=-2sinx.cosx+3x^2+6x+4\)
\(y'=\left(sinx-cosx\right)^2+3\left(x+1\right)^2\ge0\) ;\(\forall x\)
Hàm đồng biến trên R
Sắp xếp các đồng bằng duyên hải miền Trung theo thứ tự từ Nam ra Bắc *
ĐB Ninh Thuận- Bình Thuận; ĐB Bình Phú – Khánh Hòa ; ĐB Nam Ngãi ; ĐB Bình –Trị – Thiên ; ĐB Thanh – Nghệ – Tĩnh.
ĐB Ninh Thuận- Bình Thuận ; ĐB Nam Ngãi; ĐB Bình Phú – Khánh Hòa ; ĐB Bình –Trị – Thiên ; ĐB Thanh – Nghệ – Tĩnh.
ĐB Thanh – Nghệ – Tĩnh; ĐB Bình –Trị – Thiên ; ĐB Nam Ngãi; ĐB Bình Phú – Khánh Hòa; ĐB Ninh Thuận- Bình Thuận.
( Lưu ý : ĐB là đồng bằng )