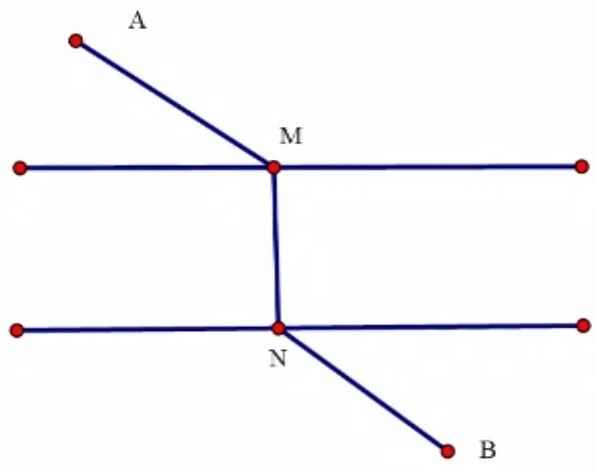
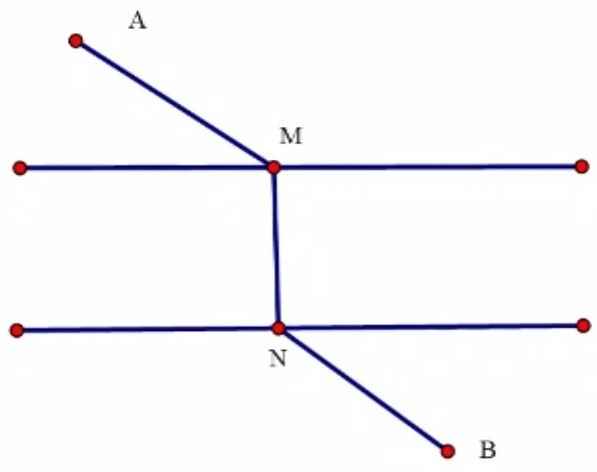
Vì MN cố định nên cần chứng minh AM+NB nhỏ nhất hay AM và NB nhỏ nhất
AM và NB nhỏ nhất \(\Leftrightarrow\) AM và BN lần lượt là hình chiếu của A,B lên các đường thẳng tương ứng
\(\Leftrightarrow\) M và N là chân đường vuông góc từ A,B đến các đường thẳng tương ứng
Vậy \(AM+MN+NB\) nhỏ nhất \(\Leftrightarrow\) M và N là chân đường vuông góc từ A,B đến các đường thẳng tương ứng
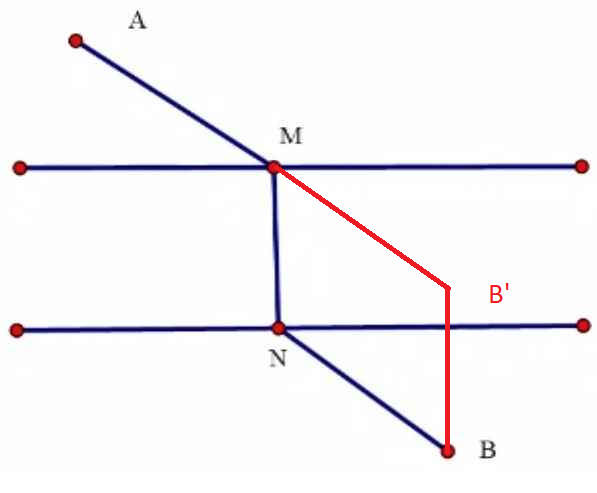AM+MN+NB nhỏ nhất, MN cố định <=> AM+NB nhỏ nhất.
Gọi T\(\overrightarrow{NM}\)(B) = B'
Có NB=MB' <=> AM + MB' nhỏ nhất <=> A,M,B' thẳng hàng
=> M là giao điểm AB' với d1
=> N là hình chiếu vuông góc của M xuống d2
