cho hỏi ![]()
công thức tìm số đối xứng trong pascal
viết chương trình đọc vào số nguyên dương n từ file văn bản sdx.inp, tìm các số đối xứng hơn bằng n, ghi kết quả ra file văn bản văn bản sdx.out trong pascal
program TimSoDoiXung;
var
f_in, f_out: text;
n, num, tmp, rem: integer;
begin
// mở file đầu vào
assign(f_in, 'sdx.inp');
reset(f_in);
// mở file đầu ra
assign(f_out, 'sdx.out');
rewrite(f_out);
// đọc n từ file đầu vào
readln(f_in, n);
// tìm các số đối xứng
for num := 1 to n do
begin
tmp := num;
rem := 0;
while tmp <> 0 do
begin
rem := rem * 10 + tmp mod 10;
tmp := tmp div 10;
end;
if num = rem then
writeln(f_out, num);
end;
// đóng file đầu vào và đầu ra
close(f_in);
close(f_out);
end.
Đồ thị hàm số có trục đối xứng là đường thẳng x=3, cắt trục tung tại điểm có tung độ bằng -16 và một trong hai giao điểm với trục hoành có hoành độ là -2. Tìm công thức của hàm số bậc hai.
Gọi công thức của hàm số bậc hai là \(y=ax^2+bx+c\)
Trục đối xứng là x=3 nên \(-\dfrac{b}{2a}=3\)
=>b=-2a
Thay x=0 và y=-16 vào (d), ta được:
\(a\cdot0^2+b\cdot0+c=-16\)
=>c=-16
=>\(y=ax^2+bx-16\)
Thay x=-2 và y=0 vào (d), ta được:
\(a\cdot\left(-2\right)^2+b\left(-2\right)-16=0\)
=>4a-2b-16=0
=>\(4a-2\cdot\left(-2a\right)=16\)
=>8a=16
=>a=2
=>b=-2a=-4
Vậy: Công thức cần tìm là \(y=2x^2-4x-16\)
Cho đồ thị hàm số bậc hai ở Hình 15.
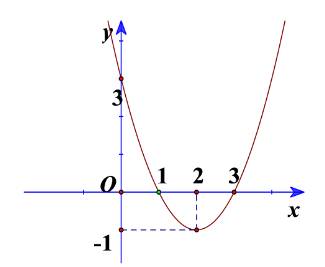
a) Xác định trục đối xứng, tọa độ đỉnh của đồ thị hàm số.
b) Xác định khoảng đồng biến, khoảng nghịch biến của hàm số.
c) Tìm công thức xác định hàm số.
a) Trục đối xứng là đường thẳng \(x = 2\)
Đỉnh là \(I\left( {2; - 1} \right)\)
b) Từ đồ thị ta thấy trên khoảng \(\left( { - \infty ;2} \right)\) thì hàm số đi xuống nên hàm số nghịch biến trên \(\left( { - \infty ;2} \right)\).
Trên khoảng \(\left( {2; + \infty } \right)\) thì hàm số đi xuống nên đồng biến trên \(\left( {2; + \infty } \right)\).
c) ) Gọi hàm số là \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)
Đồ thị hàm số có đỉnh là \(I\left( {2; - 1} \right)\) nên ta có:
\(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 2\\a{.2^2} + b.2 + c = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\4a + 2b + c = - 1\end{array} \right.\)
Ta lại có điểm \(\left( {1;0} \right)\) thuộc đồ thị nên ta có: \(a + b + c = 0\)
Vậy ta có hệ sau:
\(\left\{ \begin{array}{l}b = - 4a\\4a + 2b + c = - 1\\a + b + c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\4a + 2.\left( { - 4a} \right) + c = - 1\\a + \left( { - 4a} \right) + c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\c - 4a = - 1\\c - 3a = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\a = 1\\c = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 4\\a = 1\\c = 3\end{array} \right.\)
Vậy parabol là \(y = {x^2} - 4x + 3\)
Axit hữu cơ X mạch hở có trong quả chanh công thức phân tử là C6H8O7. Thực hiện sơ đồ phản ứng sau:
Axit xitric → + NaHCO 3 C 6 H 5 O 7 Na 3 → + Na dư C 6 H 4 O 7 Na 4
Biết X có cấu tạo đối xứng, khi cho X tác dụng với C2H5OH. Hỏi thu được bao nhiêu chất có chức este.
A. 2
B. 4
C. 5
D. 3
Cho tệp SONGUYEN.INT, chứa dãy số nguyên bất kì. Viết công thức Pascal : Đếm các số chẵn trong dãy số nguyên đó. Kết quả ghi vào tệp TONG.OUT Giúp em với ạ😔
const fi='songuyen.inp'
fo='tong.out'
var f1,f2:text;
a:array[1..100]of integer;
n,i,dem:integer;
begin
assign(f1,fi); reset(f1);
assign(f2,fo); rewrite(f2);
n:=0;
while not eof(f1) do
begin
n:=n+1;
read(f1,a[n]);
end;
dem:=0;
for i:=1 to n do
if a[i] mod 2=0 then inc(dem);
writeln(f2,dem);
close(f1);
close(f2);
end.
Hãy tìm một số hình ảnh, đồ vật trong tự nhiên có tính đối xứng (có trục đối xứng hoặc có tâm đối xứng).
số đối xứng thập phân là số j
ai vẹ với nnha
còn ai bít bài này nữa thì vẹ lun
tìm số phần tử là dương và là số đối xứng thập phân của mảng và vị trí của nó trong mang. ai học tin ấy nhé. còn ko thỉ trả lời giúp câu hỏi số đối xứng thập phân là j cx đc
Một số tự nhiên gọi là số đối xứng nếu đọc từ trái qua phải hay phải qua trái đều giống nhau, chẳng hạn số 8668. Hỏi trong phạn vi từ 1000 đến 9999 có bao nhiêu số đối xứng chia hết cho 7
in ra tất cả các số nguyên tố đối xứng có k chữ số, với k được nhập từ bàn phím (1<=k<=9)
Vd: k=3
101,131,151,181,191,313,...
Làm bằng pascal nha mn giúp mình
program abcdef;
uses Crt;
var
k, lowerLimit, upperLimit, i, j, reversed, temp, remainder: integer;
isPrime, isPalindrome: boolean;
begin
clrscr;
write('Nhap so chu so k (1<=k<=9): ');
readln(k);
lowerLimit := 1;
for i := 1 to k - 1 do
lowerLimit := lowerLimit * 10;
upperLimit := lowerLimit * 10 - 1;
writeln('Cac so nguyen to doi xung co ', k, ' chu so la:');
for i := lowerLimit to upperLimit do
begin
// Kiểm tra số nguyên tố
isPrime := True;
if i < 2 then
isPrime := False
else
for j := 2 to trunc(sqrt(i)) do
if i mod j = 0 then
beginisPrime := False;break;end;
// Kiểm tra số đối xứng
if isPrime then
begin
reversed := 0;
temp := i;
while temp <> 0 dobeginremainder := temp mod 10;
reversed := reversed * 10 + remainder;
temp := temp div 10;
end;
isPalindrome := (i = reversed);
if isPalindrome then
writeln(i);
end;
end;
readln;
end.