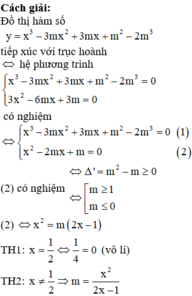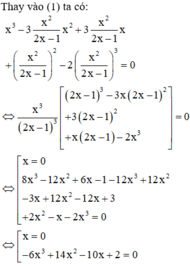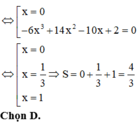Goi \(B\left(x_0;y_0\right)\) la tiep diem \(\Rightarrow x_0=1\Rightarrow y_0=3m\)

\(y'=3x^2-4x+3m\Rightarrow y'\left(1\right)=3-4+3m=3m-1\)

\(\Rightarrow pttt:y=\left(3m-1\right)\left(x-1\right)+3m\)

\(A\left(1;3\right)\in pttt\Rightarrow\left(3m-1\right)\left(1-1\right)+3m=3\Leftrightarrow3m=3\Leftrightarrow m=1\)

Phương trình hoành độ giao điểm là:

\(-\dfrac{1}{4}x^2-mx-4=0\)

\(\Leftrightarrow x^2+4mx+16=0\)

\(\Delta=\left(4m\right)^2-4\cdot1\cdot16=16m^2-64\)

Để hai đồ thị tiếp xúc với nhau thì 16m²-64=0

=>m=2 hoặc m=-2

a) vẽ bạn tự vẽ nha

b) Xét pt hoành độ giao điểm chung của (d) và (P) ta có:
\(\frac{1}{4}x^2=x+m\)

\(\Leftrightarrow x^2-4x-4m=0\left(1\right)\)

\(\Delta^,=4+4m\)

Để (d) tiếp xúc với (P) \(\Leftrightarrow\Delta^,=0\)

\(\Leftrightarrow4+4m=0\)

\(\Leftrightarrow m=-1\)

Thay m=-1 vào pt (1) ta được : 

\(x^2-4x+4=0\)

\(\Leftrightarrow\left(x-2\right)^2=0\)

\(\Leftrightarrow x=2\)

\(\Rightarrow y=\frac{1}{4}.2^2=1\)

Gọi tọa độ tiếp điểm của (d) tiếp xúc với (P) là A(x,y) 

=> tọa độ tiếp điểm là \(A\left(2;1\right)\)

\(1,m=1\Leftrightarrow y=2x+4\\ 2,\text{PT giao Ox: }y=0\Leftrightarrow\left(3m-1\right)x=-4\Leftrightarrow x=\dfrac{4}{1-3m}\Leftrightarrow A\left(\dfrac{4}{1-3m};0\right)\Leftrightarrow OA=\dfrac{4}{\left|1-3m\right|}\\ \text{PT giao Oy: }x=0\Leftrightarrow y=4\Leftrightarrow B\left(0;4\right)\Leftrightarrow OB=4\\ S_{OAB}=\dfrac{1}{2}OA\cdot OB=6\\ \Leftrightarrow\dfrac{1}{2}\cdot\dfrac{4}{\left|1-3m\right|}\cdot4=6\\ \Leftrightarrow\dfrac{8}{\left|1-3m\right|}=6\\ \Leftrightarrow\left|1-3m\right|=\dfrac{4}{3}\Leftrightarrow\left[{}\begin{matrix}1-3m=\dfrac{4}{3}\\3m-1=\dfrac{4}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=-\dfrac{1}{9}\\m=\dfrac{7}{9}\end{matrix}\right.\)

Ta có : tg60=m-1

\({\sqrt{3}=m-1} \) \(->m=\sqrt{3} +1\)

\(tan120=3-2m <=> -\sqrt{3}=3-2m \)

m=\(\frac{3+\sqrt{3}}{2}\)

Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$

$\Leftrightarrow x^2-2mx+m^2-1=0$

$\Leftrightarrow x=m+1$ hoặc $x=m-1$

Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$

Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$

$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu

$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại 

$BO=\sqrt{2}AO$

$\Leftrightarrow BO^2=2AO^2$

$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$

$\Leftrightarrow m=-3\pm 2\sqrt{2}$

Câu 2: 

Thay x=0 và y=-3 vào (d), ta được:

m+2=-3

hay m=-5