a) (C) có tâm I và đi qua M nên bán kính R = IM

Ta có: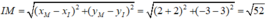 

Vậy đường tròn (C) : (x + 2)2 + (y – 3)2 = 52.

b) (C) tiếp xúc với (Δ) : x – 2y + 7 = 0

⇒ d(I; Δ) = R

Mà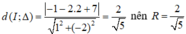 

Vậy đường tròn (C) :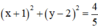 

c) (C) có đường kính AB nên (C) có :

+ tâm I là trung điểm của AB

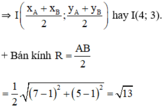
Vậy đường tròn (C) : (x – 4)2 + (y – 3)2 = 13.

Tọa độ trung điểm I của AB là: x =    − 2 + 4 2 = 1 y =    1 + ​ 1 2 = 1  

Đường tròn có tâm I(1; 1) là trung điểm của AB và có bán kính R ​ =    I A ​ =    ( − 2 − 1 ) 2 + ​ ( 1   − 1 ) 2 = 3 nên phương trình của đường tròn là:

  x − 1 2 + y − 1 2 = 9   ⇔ x 2 + y 2 − 2 x − 2 y − 7 = 0

ĐÁP ÁN C

Đáp án B

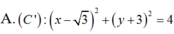
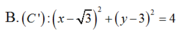
Đáp án B

- Đường tròn (C) có tâm  

và R= 4. Gọi J(a; b)  là tâm đường tròn cần tìm:

=> (C’):  (x-a)²+ (y- b)²= 4 

-Do (C) và (C’) tiếp xúc ngoài với nhau cho nên khoảng cách IJ= R+ R’

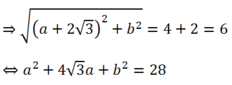
- Vì A(0;2) là tiếp điểm cho nên :  (0-a)²+ (2-b)² = 4               (2)

- Do đó ta có hệ :

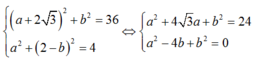
- Giải hệ tìm được: b= 3 và

Đáp án: A

A(-1;2), B(1;4)

Gọi I là trung điểm của AB ⇒ I(0;3)

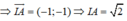
Đường tròn đường kính AB là đường tròn tâm I bán kính IA

⇒ (C): (x - 0 ) 2  + (y - 3 ) 2  = ( 2 ) 2  ⇔ x 2  + (y - 3 ) 2  = 2

Sửa:

Tâm `I` của đtr `(C)` là trung điểm của `AB`

`=>I(2;-3)`

Ta có: `R=IA=\sqrt{(3-2)^2+(-1+3)^2}=\sqrt{5}`

`=>` Ptr đtr `(C)` có tâm `I(2;-3)` và `R=\sqrt{5}` là:

         `(x-2)^2+(y+3)^2=5`

\(I\left(2;-3\right)\)

\(R=\dfrac{\sqrt{\left(3-1\right)^2+\left(1-5\right)^2}}{2}=\sqrt{5}\)

--> pt đường tròn là \(\left(x-2\right)^2+\left(x+3\right)^2=5\)

(x - 2 ) \(^2\)+(y + 3)\(^2\)  =5

Gọi I là trung điểm AB \(\Rightarrow I\left(2;-3\right)\Rightarrow\overrightarrow{IA}=\left(1;2\right)\Rightarrow IA=\sqrt{1^2+2^2}=\sqrt{5}\)

Đường tròn đường kính AB nhận I là tâm và có bán kính R=IA nên có pt:

\(\left(x-2\right)^2+\left(y+3\right)^2=5\)

Tọa độ tâm là:

\(\left\{{}\begin{matrix}x_O=\dfrac{1+7}{2}=4\\y_O=\dfrac{1+5}{2}=3\end{matrix}\right.\)

Vậy: Tọa độ tâm là O(4;3)

\(OA=\sqrt{\left(4-1\right)^2+\left(3-1\right)^2}=\sqrt{13}\)

Phương trình đường tròn là:

\(\left(x-4\right)^2+\left(y-3\right)^2=13\)

a) Đường tròn (C) tâm \(I(1;5)\), bán kính \(r = 4\) có phương trình là: \({\left( {x - 1} \right)^2} + {\left( {y - 5} \right)^2} = 16\)

b) \(MN = \sqrt {{{\left( {9 - 3} \right)}^2} + {{\left( {3 - ( - 1)} \right)}^2}}  = 2\sqrt {13} \), suy ra bán kính là \(\sqrt {13} \)

Tâm của đường tròn là trung điểm của MN: \(I(6;1)\)

Đường tròn (C) tâm \(I\left( {6;1} \right)\)và bán kính là \(\sqrt {13} \) có phương trình: \({\left( {x - 6} \right)^2} + {\left( {y - 1} \right)^2} = 13\)

c) Ta có bán kính của đường tròn \(r = d\left( {I,d} \right) = \frac{{\left| {5.2 - 12.1 + 11} \right|}}{{\sqrt {{5^2} + {{12}^2}} }} = \frac{9}{{13}}\)

Đường tròn (C) tâm \(I\left( {2;1} \right)\)và bán kính là \(\frac{9}{{13}}\) có phương trình: \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{81}}{{169}}\)

d) Bán kính của đường tròn là \(r = AB = \sqrt {{{\left( {4 - 1} \right)}^2} + {{\left( {( - 5) - ( - 2)} \right)}^2}}  = 3\sqrt 2 \)

Đường tròn (C) tâm \(A(1; - 2)\)và bán kính là \(3\sqrt 2 \) có phương trình: \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 18\)