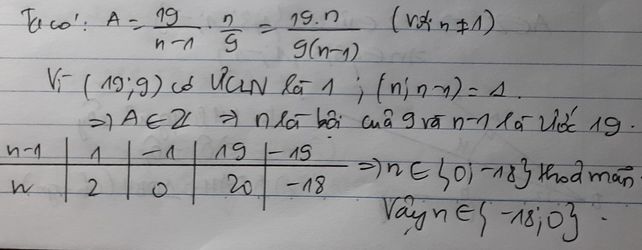Tìm n \(\in Z\) A=\(\dfrac{n+1}{n-2}\)(n\(\ne\) 2) có giá trị nguyên

Những câu hỏi liên quan
Tìm số nguyên n để A=\(\dfrac{n+1}{n-2}\)có giá trị nguyên, với n\(\ne\)2
để a là số nguyên thì n+1⋮n-2
n-2+3⋮n-2
n-2⋮n-2 ⇒ 3⋮n-2 n-2∈Ư(3)
Ư(3)={1;3;-1;-3}
Vậy n ∈{3;5;1;-1}
Đúng 2
Bình luận (1)
Để A là số nguyên thì \(n+1⋮n-2\)
\(\Leftrightarrow n-2+3⋮n-2\)
mà \(n-2⋮n-2\)
nên \(3⋮n-2\)
\(\Leftrightarrow n-2\inƯ\left(3\right)\)
\(\Leftrightarrow n-2\in\left\{1;-1;3;-3\right\}\)
hay \(n\in\left\{3;1;5;-1\right\}\)(thỏa ĐK)
Vậy: Để A nguyên thì \(n\in\left\{3;1;5;-1\right\}\)
Đúng 2
Bình luận (0)
ta có :n+1/n-2=n-2+3
=>n+1 thuộc Ư(3)
=> n +1 thuộc{1;3;-1;-3}
ta có bảng:
| n+1 | 1 | -1 | -3 | 3 |
| n | 0 | -2 | -4 | 2 |
ĐK | tm | tm | tm | tm |
Đúng 1
Bình luận (0)
Cho phân số A=\(\dfrac{n+1}{n-3}\) (n\(\in\)Z)
a, Tìm các giá trị của n để A là phân số.
b, Tìm n để A có giá trị nguyên.
a, Để A là phân số khi n - 3 \(\ne\)0<=> n \(\ne\)3
b, Để A nguyên khi \(n+1⋮n-3\Leftrightarrow n-3+4⋮n-3\Leftrightarrow4⋮n-3\)
\(\Rightarrow n-3\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
| n - 3 | 1 | -1 | 2 | -2 | 4 | -4 |
| n | 4 | 2 | 5 | 1 | 7 | -1 |
Đúng 2
Bình luận (0)
a) Để A là phân số thì \(n-3\ne0\)
hay \(n\ne3\)
b) Để A là số nguyên thì \(n+1⋮n-3\)
\(\Leftrightarrow4⋮n-3\)
\(\Leftrightarrow n-3\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{4;2;5;1;7;-1\right\}\)
Đúng 0
Bình luận (0)
Cho A=\(\frac{2n}{n-2}\)(n\(\in\)Z ,n\(\ne\)0).Tìm số nguyên n để A là giá trị nguyên
Ta có: \(A=\frac{2n}{n-2}\Rightarrow n>0\)
Lập luận
+ n lớn hơn không vì nếu n nhỏ hơn 0 thì \(\frac{2n}{n-2}\)sẽ trở thành \(\frac{2\left(-n\right)}{n-2}\) (vô lý)
=> n thuộc tập N*
Đúng 0
Bình luận (0)
Tìm tất cả các số nguyên n sao cho các phân số sau có giá trị là số nguyên:
\(\dfrac{4}{n+2}\) (n\(\ne\)-2)
Với n≠-2,n∈Z. Để 4/n+2 có giá trị là số nguyên thì 4⋮n+2
⇒n+2 ∈ Ư(4)={1;2;4;-1;-2;-4}
Nếu n+2=1⇒n=-1(TMĐK)
Nếu n+2=2⇒n=0(TMĐK)
Nếu n+2=4⇒n=2(TMĐK)
Nếu n+2=-1⇒n=-3(TMĐK)
Nếu n+2=-2⇒n=-4(TMĐK)
Nếu n+2=-4⇒n=-6(TMĐK)
Vậy với n ∈ {-1;0;2;-3;-4;-6} thì 4/n+2 có giá trị nguyên.
Đúng 1
Bình luận (2)
Tìm n\(\in\) Z để tích hai phân số \(\dfrac{19}{n-1}\)với (n\(\ne1\)) và \(\dfrac{n}{9}\)có giá trị là số nguyên
Để tích 2 PS là số nguyên thì 19⋮n-1 và n⋮9
⇒n-1∈Ư(19),9∈B(n)
⇒Ư(19)={\(\pm\)1;\(\pm\)19}
⇒n-1=1 ⇒n-1=19
⇒n-1=-1 ⇒n-1=-19
⇒n∈{2;20;0;-18} nhưng 9∈B(n)
⇒n∈{0;-18}
Đúng 0
Bình luận (0)
Giải:
Ta gọi tích hai số là A
Ta có:
\(A=\dfrac{19}{n-1}.\dfrac{n}{9}=\dfrac{19.n}{\left(n-1\right).9}\) (với n ≠ 1)
Vì \(ƯCLN\left(19;9\right)=1\) \(;ƯCLN\left(n;n-1\right)=1\)
\(\Rightarrow A\in Z\)
\(\Rightarrow n\in B\left(9\right)\) và \(\left(n-1\right)\inƯ\left(19\right)\)
Ta có bảng giá trị:
| n-1 | 1 | -1 | 19 | -19 |
| n | 2 | 0 | 20 | -18 |
\(\Rightarrow n\in\left\{-18;0\right\}\) (t/m)
Vậy \(n\in\left\{-18;0\right\}\)
Đúng 0
Bình luận (0)
Bài 1:
Tìm số nguyên n để phân số A= \(\dfrac{1}{n+3}\)có giá trị nguyên
Bài 2 : Tìm số nguyên n để phân số B = \(\dfrac{n+4}{n+1}\)có giá trị nguyên
bài 1
để A∈Z
\(=>n+3\inƯ\left(1\right)=\left\{-1;1\right\}\)
\(=>\left\{{}\begin{matrix}n+3=-1\\n+3=1\end{matrix}\right.=>\left\{{}\begin{matrix}n=-4\\n=-2\end{matrix}\right.\)
vậy \(n\in\left\{-4;-2\right\}\) thì \(A\in Z\)
Đúng 4
Bình luận (0)
Để A nguyên
⇒ \(\left(n+3\right)\inƯ\left(1\right)=\left\{\pm1\right\}\)
n+3 1 -2
n -2 -4
Đúng 2
Bình luận (0)
\(B=\dfrac{n+3+1}{n+1}=1+\dfrac{3}{n+1}\)
Để B nguyên
\(\Rightarrow\left(n+1\right)\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
n+1 1 -1 3 -3
n 0 -2 2 -4
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho phân số: A= \(\frac{n+1}{n-2}\)
a, Tìm \(n\in Z\) để A có giá trị nguyên
b,Tìm \(n\in Z\) để A có giá trị lón nhất
\(A=\frac{n+1}{n-2}=\frac{n-2+2+1}{n-2}=\frac{n-2+3}{n-2}=\frac{n-2}{n-2}+\frac{3}{n-2}=2+\frac{3}{n-2}\)
Để A là số nguyên thì \(\frac{3}{n-2}\)là số nguyên
\(\frac{3}{n-2}\)là 1 số nguyên khi và chỉ khi \(n-2\)là ước của 3
\(\Rightarrow n-2=\left(-1;1;-3;3\right)\)
\(n-2=1\Rightarrow n=1+2=3\)
\(n-2=\left(-1\right)\Rightarrow n=\left(-1\right)+2=1\)
\(n-2=3\Rightarrow n=3+2=5\)
\(n-2=\left(-3\right)\Rightarrow n=\left(-3\right)+2=\left(-1\right)\)
Vậy \(n\)là \(3;1;5;\left(-1\right)\)để A là phân số
Đúng 0
Bình luận (0)
Xin lổi
Để A là giá trị lớn nhất nhé ! nhưng vẩn nhớ k cho tớ nhé
Đúng 0
Bình luận (0)
a) Ta có : \(\frac{n+1}{n-2}=\frac{\left(n-2\right)+2+1}{n-2}=\frac{\left(n-2\right)+3}{n-2}=\frac{n-2}{n-2}+\frac{3}{n-2}=1+\frac{3}{n-2}\)
Để \(n+1⋮n-2\Leftrightarrow\frac{3}{n-2}\in Z\Leftrightarrow3⋮n-2\Leftrightarrow n-2\inƯ\left(3\right)=\left\{-1;1;-3;3\right\}\)
* Với n - 2 = 1 => n = 2 +1 = 3 ( thỏa mãn )
* Với n - 2 = -1 => n = -1 + 2 = 1 ( thỏa mãn )
* Với n - 2 = 3 => n = 3 + 2 = 5 ( thỏa mãn )
* Với n - 2 = -3 => -3 + 2 = -1 ( thỏa mãn )
Vậy với \(n\in\left\{3;1;5;-1\right\}\)thì A có giá trị số nguyên
b) Để A có giá trị lớn nhất thì n = 3
Đúng 0
Bình luận (0)
Cho Biểu Thức A= \(\dfrac{3n+2}{n+1}\) (n∈Z,n≠ -1).Tìm giá trị n để A có giá trị nguyên
GIÚP EM VỚI
Để A nguyên thì 3n+3-1 chia hết cho n+1
=>\(n+1\in\left\{1;-1\right\}\)
=>\(n\in\left\{0;-2\right\}\)
Đúng 0
Bình luận (0)
Cho phân số C=\(\frac{2n+7}{n+2}\)\(\left(n\in Z,n\ne-3\right)\). Tìm các giá trị của n để D là số nguyên?
Để Dlaf số nguyên
-) 2n+7 chia hết n+3
n+3 chia hết n+3 vậy 2(n+3)chia hết n+3
vậy 2n +6 chia hết n+3
suy ra (2n+7)-(2n+6)chia hết n+3
suy ra 1 chia hết n+3
vậy n+3 = 1 hoặc -1
suy ra n= -2 hoặc -4 k đúbg mk nha
Ta có : \(\frac{2n+7}{n+3}=\frac{2n+6+1}{n+3}=\frac{2\left(n+3\right)+1}{n+3}=2+\frac{1}{n+3}\)
Để \(C\inℤ\Rightarrow\frac{1}{n+3}\inℤ\Rightarrow1⋮n+3\Rightarrow n+3\inƯ\left(1\right)\)
mà \(n\inℤ\Rightarrow n+3\inℤ\)
Khi đó \(n+3\in\left\{1;-1\right\}\Rightarrow n\in\left\{-2;-4\right\}\)
C = (2n+6+1) / (n+3)
C = 2 +1/n+3
Để C thì n+3 thuộc ước của 1
Suy ra n+3 = (1;-1)
Vậy n = (-2;-4)
Xem thêm câu trả lời