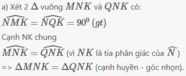cho tam giác MNP vuông tại M biết M N = 6 cm N P = 10 cm Tính độ dài MP

Những câu hỏi liên quan
1. Cho tam giác MNP cân tại M vẽ MH thuộc NP (H thuộc NP)a) Chứng minh NH PHb) Cho MH 4 cm; NH 3 cm. Tính MN2. Cho tam giác MNP vuông tại M, có góc N 60o và MN 5 cm. Tia phân giác của góc N cắt MP tại D. Kẻ DE vuông góc với PN tại Ea) Chứng minh: tam giác MNP tam giác ENDb) Chứng minh: tam giác MNE là tam giác đềuc) Tính độ dài cạnh PN3. Cho tam giác MNP cân tại M, góc M 30o; NP 2 cm. Trên cạnh MP lấy điểm Q sao cho góc PNQ 60o. Tính độ dài MQ
Đọc tiếp
1. Cho tam giác MNP cân tại M vẽ MH thuộc NP (H thuộc NP)
a) Chứng minh NH = PH
b) Cho MH = 4 cm; NH = 3 cm. Tính MN
2. Cho tam giác MNP vuông tại M, có góc N = 60o và MN = 5 cm. Tia phân giác của góc N cắt MP tại D. Kẻ DE vuông góc với PN tại E
a) Chứng minh: tam giác MNP = tam giác END
b) Chứng minh: tam giác MNE là tam giác đều
c) Tính độ dài cạnh PN
3. Cho tam giác MNP cân tại M, góc M = 30o; NP = 2 cm. Trên cạnh MP lấy điểm Q sao cho góc PNQ = 60o. Tính độ dài MQ
Câu 10. Cho tam giác MNP vuông tại M, đường cao MH, phân giác MD. Biết MN = 72 cm, MP = 96 cm. Độ dài NH, MH, HD là
Gấp !!!
(Tự vẽ hình)
- Xét △MNP vuông tại M, áp dụng định lí Pytago:
\(^{NM^2}\)+\(MP^2\)=\(NP^2\)
=\(72^2\)+\(96^2\)=\(NP^2\)
⇔\(NP^2\)=\(72^2\)+\(96^2\)=14400
⇔\(NP\)=\(\sqrt{14400}\)=120cm
- Xét △MNP vuông tại M, đường cao MH, theo hệ thức lượng ta có:
\(MN^2\)=\(NH.NP\)
\(72^2\)=\(NH.120\)
⇔\(NH\)=\(\dfrac{72^2}{120}\)=43,2 cm
- \(MH.NP\)=\(MP.MN\)
⇔ \(MH\)=\(\dfrac{MP.MN}{NP}\)=\(\dfrac{96.72}{120}\)=3,6cm
Đúng 0
Bình luận (0)
Giúp mik vs:<
Cho MNP cân tại M, kẻ PH ⊥ MN (H thuộc MN) biết MP = 10 cm và PH = 6 cm. Tính độ dài cạnh đáy của tam giác cân.
Xét tam giác MHP vuông tại H có:
\(MH^2+HP^2=MP^2\left(Pytago\right)\)
\(\Rightarrow MH^2+6^2=10^2\Rightarrow MH=8\left(cm\right)\)
Mà \(MH+HN=MN=MP=10cm\)(do tam giác MNP cân tại M)
\(\Rightarrow8+HN=10\Rightarrow HN=2\left(cm\right)\)
Xét tam giác NHP vuông tại H có:
\(HN^2+HP^2=NP^2\left(Pytago\right)\)
\(\Rightarrow2^2+6^2=NP^2\Rightarrow NP=2\sqrt{10}\left(cm\right)\)
Đúng 2
Bình luận (1)
Cho tam giác MNP cân tại M có MP=3,5 cm, góc N=58 độ. Kẻ NG vuông góc với MP tại Q. Tinh độ dài NQ
Bài 5 (1 điểm): Cho tam giác MNP vuông tại M, có MN = 6 cm, MP = 8 cm. Chứng minh rằng các
đỉnh M, N, P cùng thuộc một đường tròn. Hãy xác định tâm và tính độ dài bán kính của đường tròn
đó.
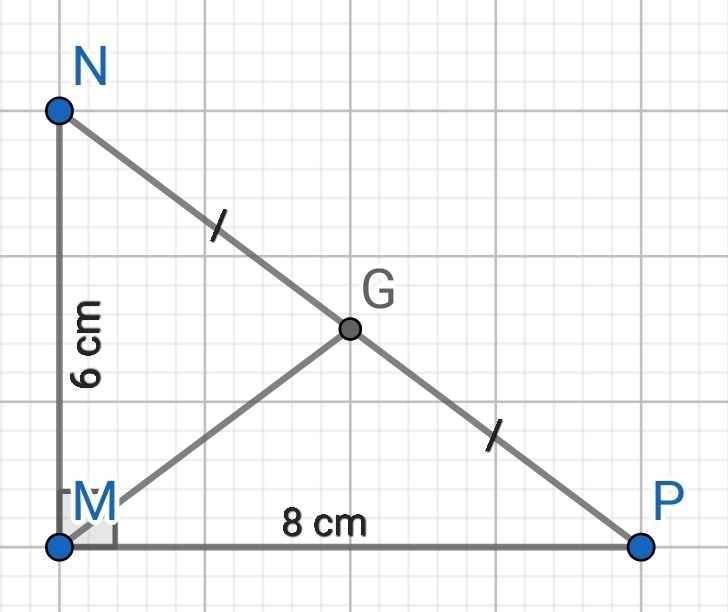
Ta có:
∆MNP vuông tại M
⇒ NP² = MP² + MN² (Pytago)
= 8² + 6² = 100
⇒ NP = 10 (cm)
Gọi G là trung điểm của NP
⇒ MG là đường trung tuyến ứng với cạnh huyền NP của ∆MNP
⇒ MG = NG = PG = NP : 2 = 5 (cm)
⇒ M, N, P cùng thuộc đường tròn tâm G, bán kính MG = 5 cm
Đúng 1
Bình luận (0)
Stshdtgfdrsgettgstgefdfe📱📱📱📱📱📱💻📱📱📱📱📱📱📱📱💻💻💻💻💻💻📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱🖍️🖍️📱📱📱📱📱📱📱📱📱📱💻📱💻📱💻📱💻📱💻📱💻📱💻📱💻📱💻📱📱💻💻📱💻📱💻📱💻📱📱💻💻📱📱💻📱💻📱💻📱💻📱📱💻📱📱📱📱📱📱📱💻📱💻📱📱💻📱📱📱💻📱💻📱📱📱📱📱📱💻💻💻💻📱📱📱📱
Đúng 0
Bình luận (0)
CHO tam giácMNP vuông tại M, có góc N=60o và MN =5cm. Tia phân giác của góc N cắt MP tại D kẻ DE vuông PN tại C
A)cm: tam giác MNP = tam giác END
b)CM: tam giác MNE là tam giác đều
c) Tính độ dài cạnh PN
cho tam giác MNP vuông tại M,góc N=60 độ ,MN=8cm, MP=8cm.Tia phân giác MNP cắt MP tại K. Kẻ KH vuông với NP tại H
a) Tính NP
b) Cm Tam giác MNK=HNK
c) Tam giác MNH là tam giác gì? Why?
giúp mình với
cho tam giác MNP vuông tại M,góc N=60 độ ,MN=8cm, MP=8cm.Tia phân giác MNP cắt MP tại K. Kẻ KH vuông với NP tại H
a) Tính NP
b) Cm Tam giác MNK=HNK
c) Tam giác MNH là tam giác gì? Why?
giúp mình với
Cho tam giác MNP vuông ở M, MN = 6 cm, MP = 8 cm. Vẽ hình. a,Tính NP,N;P. b, Phân giác của góc M cắt NP tại E. Tính NE, PE.
a: NP=10(cm)
\(\widehat{P}=37^0\)
\(\widehat{N}=53^0\)
Đúng 1
Bình luận (0)
a, \(NP=\sqrt{MN^2+MP^2}=10\left(cm\right)\)
\(\sin N=\dfrac{MP}{NP}=\dfrac{4}{5}\approx\sin53^0\Rightarrow\widehat{N}\approx53^0\\ \widehat{P}=90^0-\widehat{N}\approx37^0\)
b, \(\dfrac{NE}{PE}=\dfrac{MN}{MP}=\dfrac{3}{4}\Rightarrow NE=\dfrac{3}{4}PE\)
\(NE+PE=NP=10\Rightarrow\dfrac{7}{4}PE=10\Rightarrow\left\{{}\begin{matrix}PE=\dfrac{40}{7}\left(cm\right)\\NE=\dfrac{30}{7}\left(cm\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)