Khi x = 4; hàm số y = ax - 1 có giá trị bằng - 3 . giá trị của a bằng :
A
1
B -1
C 2
D.Một kết quả khác
Những câu hỏi liên quan
lim\(\dfrac{2-\sqrt{4-x}}{x}\) khi x->0
lim\(\dfrac{x^3+8}{x^2-4}\) khi x->-2
Lời giải:
\(\lim\limits_{x\to 0}\frac{2-\sqrt{4-x}}{x}=\lim\limits_{x\to 0}\frac{4-(4-x)}{x(2+\sqrt{4-x})}=\lim\limits_{x\to 0}\frac{x}{x(2+\sqrt{4-x})}=\lim\limits_{x\to 0}\frac{1}{2+\sqrt{4-x}}=\frac{1}{4}\)
\(\lim\limits_{x\to -2}\frac{x^3+8}{x^2-4}=\lim\limits_{x\to -2}\frac{(x+2)(x^2-2x+4)}{(x-2)(x+2)}=\lim\limits_{x\to -2}\frac{x^2-2x+4}{x-2}=-3\)
Đúng 1
Bình luận (0)
Tìm m để hàm số
f
x
x
2
-
16
x
-
4
k
h
i...
Đọc tiếp
Tìm m để hàm số f x = x 2 - 16 x - 4 k h i x > 4 m x + 1 k h i x ≤ 4 liên tục tại điểm x = 4
A. m = -8
B. m = 8
C. m = - 7 4
D. m = 7 4
Tìm tham số thực m để hàm số
y
f
(
x
)
x
2
+
x
-
12
x
+
4...
Đọc tiếp
Tìm tham số thực m để hàm số y = f ( x ) = x 2 + x - 12 x + 4 k h i x k h a c - 4 m x + 1 k h i x = - 4 liên tục tại điểm x=-4
A. m=4
B. m=3
C. m=2
D. m=5
Cho hàm số
f
(
x
)
x
-
2
x
-
4
K
h
i
...
Đọc tiếp
Cho hàm số f ( x ) = x - 2 x - 4 K h i x ≠ 4 1 4 K h i x = 4 . Khẳng định nào sau đây đúng nhất
A. Hàm số liên tục tại x = 4
B. Hàm số liên tục tại mọi điểm trên tập xác định nhưng gián đoạn tại x = 4
C. Hàm số không liên tục tại x = 4
D. Tất cả đều sai
Chọn C.
Ta có :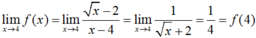 
Hàm số liên tục tại điểm x = 4.
Đúng 0
Bình luận (0)
Tìm tham số thực m để hàm số
y
f
(
x
)
x
2
+
x
-
12
x
+
4...
Đọc tiếp
Tìm tham số thực m để hàm số y = f ( x ) = x 2 + x - 12 x + 4 k h i x ≠ - 4 m x + 1 k h i x = - 4 liên tục tại điểm x 0 = - 4
A. m=4.
B. m=3.
C. m=2.
D. m=5.
Thu gọn:
A= 3|x|-(1-2x) khi x<0
B=|x-3|+4-x khi x<3
C=|5|-(2-x) khi x<5
E=(x-3):|2x-6| khi x>3
Tìm tham số thực m để hàm số
y
f
x
x
2
+
x
−
12
x
+
4
...
Đọc tiếp
Tìm tham số thực m để hàm số y = f x = x 2 + x − 12 x + 4 khi x ≠ − 4 m x + 1 khi x = 4 liên tục tại điểm x 0 = − 4
A. m = 4
B. m = 3
C. m = 2
D. m = 5
Hàm số
f
x
x
2
−
16
x
−
2
k
h
i...
Đọc tiếp
Hàm số f x = x 2 − 16 x − 2 k h i x > 4 3 x − m k h i x ≤ 4 liên tục tại x 0 = 4 khi m nhận giá trị là
A. 44
B. -20
C. 20
D. m bất kỳ
Đáp án B
Ta có: lim x → 4 − f x = lim x → 4 − 3 x − m = 12 − m
lim x → 4 + f x = lim x → 4 + x 2 − 16 x − 2 = lim x → 4 + x − 4 x + 4 x + 2 x − 4 = lim x → 4 + x + 4 x + 2 = 32
Để hàm số liên tục tại x = 4 thì lim x → 4 − f x = lim x → 4 + f x = f 4 ⇔ 12 − m = 32 ⇔ m = − 10
Đúng 0
Bình luận (0)
cho lim \(\dfrac{f\left(x\right)-5}{x-1}=4\) khi x->1 , lim \(\dfrac{g\left(x\right)-1}{x-1}=5\) khi x->1
tinh lim \(\dfrac{\sqrt{f\left(x\right)\times g\left(x\right)+4}-1}{x-1}\)khi x->1
Bạn tham khảo:
Nếu \(lim\) (x->1) \(\dfrac{f\left(x\right)-5}{x-1}=2\) và lim (x->1) \(\dfrac{g\left(x\right)-1}{x-1}=3\) thì lim (x->1... - Hoc24
Không giống hoàn toàn, nhưng cách làm thì giống hoàn toàn
Đúng 2
Bình luận (0)
Bài 1 trang 84 SGK Toán 11 tập 1 - Chân trời sáng tạo
17 tháng 7 2023 lúc 14:37
Một bãi đậu xe ô tô đưa ra giá \(C\left( x \right)\) (đồng) khi thời gian đậu xe là \(x\) (giờ) như sau:
\(C\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{60000}&{khi\,\,0 < x \le 2}\\{100000}&{khi{\rm{ }}2 < x \le 4}\\{200000}&{khi{\rm{ }}4 < x \le 24}\end{array}} \right.\)
Xét tính liên tục của hàm số \(C\left( x \right)\).
Hàm số \(C\left( x \right)\) có tập xác định là nửa khoảng \(\left( {0;24} \right]\).
Hàm số \(C\left( x \right)\) xác định trên từng khoảng \(\left( {0;2} \right),\left( {2;4} \right)\) và \(\left( {4;24} \right)\) nên hàm số liên tục trên các khoảng đó.
Ta có: \(C\left( 2 \right) = 60000\)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} C\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} 100000 = 100000\\\mathop {\lim }\limits_{x \to {2^ - }} C\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} 60000 = 60000\end{array}\)
Vì \(\mathop {\lim }\limits_{x \to {2^ + }} C\left( x \right) \ne \mathop {\lim }\limits_{x \to {2^ - }} C\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to 2} C\left( x \right)\).
Vậy hàm số \(C\left( x \right)\) không liên tục tại điểm \({x_0} = 2\).
Ta có: \(C\left( 4 \right) = 100000\)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {4^ + }} C\left( x \right) = \mathop {\lim }\limits_{x \to {4^ + }} 200000 = 200000\\\mathop {\lim }\limits_{x \to {4^ - }} C\left( x \right) = \mathop {\lim }\limits_{x \to {4^ - }} 100000 = 100000\end{array}\)
Vì \(\mathop {\lim }\limits_{x \to {4^ + }} C\left( x \right) \ne \mathop {\lim }\limits_{x \to {4^ - }} C\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to 4} C\left( x \right)\).
Vậy hàm số \(C\left( x \right)\) không liên tục tại điểm \({x_0} = 4\).
Ta có: \(C\left( {24} \right) = 200000\)
\(\mathop {\lim }\limits_{x \to {{24}^ - }} C\left( x \right) = \mathop {\lim }\limits_{x \to {{24}^ - }} 200000 = 200000 = C\left( {24} \right)\)
Vậy hàm số \(C\left( x \right)\) liên tục trái tại điểm \({x_0} = 24\).
Vậy hàm số \(C\left( x \right)\) liên tục trên các khoảng \(\left( {0;2} \right),\left( {2;4} \right)\) và nửa khoảng \(\left( {4;24} \right]\).
Đúng 0
Bình luận (0)