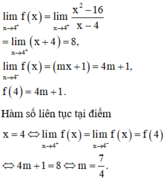Các câu hỏi tương tự
Tìm tham số thực m để hàm số
y
f
(
x
)
x
2
+
x
-
12
x
+
4...
Đọc tiếp
Tìm tham số thực m để hàm số y = f ( x ) = x 2 + x - 12 x + 4 k h i x k h a c - 4 m x + 1 k h i x = - 4 liên tục tại điểm x=-4
A. m=4
B. m=3
C. m=2
D. m=5
Cho hàm số y f(x) liên tục trên R sao cho
m
a
x
x
∈
0
;
10
f
(
x
)
f
(
2
)
4
. Xét hàm số
g
(
x
)
f
(
x...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R sao cho m a x x ∈ 0 ; 10 f ( x ) = f ( 2 ) = 4 . Xét hàm số g ( x ) = f ( x 3 + x ) − x 2 + 2 x + m . Giá trị của tham số m để m a x x ∈ 0 ; 2 g ( x ) = 8 là
A. 5
B. 4
C. -1
D. 3
Tìm tham số thực m để hàm số
y
f
x
x
2
+
x
−
12
x
+
4
...
Đọc tiếp
Tìm tham số thực m để hàm số y = f x = x 2 + x − 12 x + 4 khi x ≠ − 4 m x + 1 khi x = 4 liên tục tại điểm x 0 = − 4
A. m = 4
B. m = 3
C. m = 2
D. m = 5
Tìm tham số thực m để hàm số
y
f
x
x
2
+
x
−
12
x
+
4
khi...
Đọc tiếp
Tìm tham số thực m để hàm số y = f x = x 2 + x − 12 x + 4 khi x ≠ − 4 mx + 1 khi x = − 4 liên tục tại điểm x 0 = − 4 .
A. m = 4
B. m = 3
C. m = 5
D. m = 2
Tìm tất cả các giá trị thức của tham số m để hàm số
f
(
x
)
x
2
-
16
x
-
4
k...
Đọc tiếp
Tìm tất cả các giá trị thức của tham số m để hàm số f ( x ) = x 2 - 16 x - 4 k h i x > 4 m x + 1 k h i x ≤ 4 liên tục trên R
A. m=8 hoặc m = - 7 4
B. m = 7 4
C. m = - 7 4
D. m=-8 hoặc m = 7 4
Cho hàm số
f
(
x
)
1
+
c
o
s
x
(
x
-
π
)...
Đọc tiếp
Cho hàm số f ( x ) = 1 + c o s x ( x - π ) 2 k h i x ≠ π m k h i x = π Tìm m để f(x) liên tục tại x = π
A. m = 1 4
B. m = - 1 4
C. m = 1 2
D. m = - 1 2
Tìm giá trị cực đại của tham số m để hàm số
f
x
x
+
1
...
Đọc tiếp
Tìm giá trị cực đại của tham số m để hàm số f x = x + 1 khi x > 2 x 2 + m khi x ≤ 2 liên tục tại điểm x=2?
A. m= -1.
B. m= 0.
C. m= 3.
D. m= -6.
Cho hàm số f(x) có đạo hàm liên tục trên khoảng K và có đồ thị là đường cong (C). Viết phương trình tiếp tuyến của (C) tại điểm M(a;f(a)), (aϵ K). A. yf’(a)(x-a)-f(a). B. yf’(a)(x+a)+f(a). C. yf(a)(x-a)+f’(a). D. yf’(a)(x-a)+f(a).
Đọc tiếp
Cho hàm số =f(x) có đạo hàm liên tục trên khoảng K và có đồ thị là đường cong (C). Viết phương trình tiếp tuyến của (C) tại điểm M(a;f(a)), (aϵ K).
A. y=f’(a)(x-a)-f(a).
B. y=f’(a)(x+a)+f(a).
C. y=f(a)(x-a)+f’(a).
D. y=f’(a)(x-a)+f(a).
Cho hàm số
f
x
x
−
8
x
−
2
k
h
i
x
≠...
Đọc tiếp
Cho hàm số f x = x − 8 x − 2 k h i x ≠ 2 2 m + 1 k h i x = 2 . Tìm m để hàm số liên tục tại điểm x 0 = 2 .
A. 3/2
B. 13/2
C. 11/2
D. -1/2