Chọn C.
Ta có : 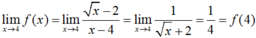
Hàm số liên tục tại điểm x = 4.
Chọn C.
Ta có : 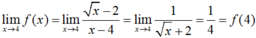
Hàm số liên tục tại điểm x = 4.
Cho hàm số f ( x ) = x 2 - 4 Chọn câu đúng trong các câu sau: Cho hàm sô f(x) = căn bậc hai x^2 - 4
(I) f(x) liên tục tại x = 2.
(II) f(x) gián đoạn tại x = 2
(III) f(x) liên tục trên đoạn [-2; 2].
A. Chỉ (I) và (III).
B. Chỉ (I).
C. Chỉ (II).
D. Chỉ (II) và (III).
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = ( x + 1 ) 4 ( x - 2 ) 5 ( x + 3 ) 3 . Số điểm cực trị của hàm số f ( x ) là:
A. 5
B. 3
C. 1
D. 2
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = ( x + 1 ) 4 ( x - 2 ) 5 ( x + 3 ) 3 . Số điểm cực trị của hàm số f ( x ) là:
A. 5
B. 3
C. 1
D. 2
1. đạo hàm của hàm số f(x) = 2x - 5 tại \(x_0=4\)
2. đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
3. đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
Cho hàm số f ( x ) = 4 - x 2 - 2 ≤ x ≤ 2 1 x > 2 . Tìm khẳng định đúng trong các khẳng định sau:
(I) f(x) không xác định tại x = 3
(II) f(x) liên tục tại x = -2
(III) lim x → 2 f ( x ) = 2
A. Chỉ (I).
B. Chỉ (I) và (II).
C. Chỉ (I) và (III).
D. Cả (I); (II); (III) đều sai.
1) đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
2) đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó:
a) f(x)=x2+sinx;
b) g(x)=x4−x2+\(\dfrac{6}{x-1}\);
c) h(x)=`(2x)/(x−3)+(x−1)/(x+4)`.
Cho hàm số f(x) = 5(x + 1)3 + 4(x + 1). Tập nghiệm của phương trình f ”(x) = 0 là
A. [-1 ; 2] .
B. -1.
C. {-1}.
D. ∅.
Cho hàm số f ( x ) = 5 ( x + 1 ) 3 + 4 ( x + 1 ) . Tập nghiệm của phương trình f ' ' ( x ) = 0 là
A. [-1;2]
B. ( - ∞ ; 0 ]
C. {1}
D. ∅
Cho hàm số y = f(x) – cos2x với f(x) là hàm số liên tục trên R . Trong 4 biểu thức dưới đây, biểu thức nào xác định f(x) thỏa mãn y’ = 1, ∀ x ∈ R?
A. x + 1 2 cos 2 x
B. x - 1 2 cos 2 x
C. x – sin2x
D. x + sin2x