Tam giác ABC vuông tại A. Kẻ AH\(\perp\) BC.
Chứng minh: a, B = HAC; b, C = HAB
cho tam giác abc vuông tại a. kẻ ah vuông góc với bc (h thuộc bc) a) chứng minh B=HAC b)các tia phân giác của ABC vadf HAC cắt nhau tại k chứng minh tam giác AKB vuông tại k
Cho tam giác ABC vuông tại A.Từ A kẻ AH vuông BC.Tia phân giác góc HAC cắt BC tại D.Từ D kẻ DK vuông AC. Chứng minh a)AH=AK b)AC+AB<BC+AH
Cho tam giác ABC vuông tại A.Từ A kẻ AH vuông BC.Tia phân giác góc HAC cắt BC tại D.Từ D kẻ DK vuông AC. Chứng minh a)AH=AK b)AC+AB<BC+AH
Bài tập 95: Cho tam giác ABC vuông tại A, kẻ \(AH\perp BC\) tại H . Lấy điểm E đối xứng với điểm H qua AB và lấy điểm F đối xứng với điểm H qua AC
a, Chứng minh: E, A, F thẳng hàng
b, Chứng minh:\(AH^2=HB.HC\)
Bài tập 130: Cho tam giác ABC vuông tại A, kẻ \(AH\perp BC\) tại H. Tia phân giác của góc HAC cắt BC tại D, tia phân giác của góc HAB cắt BC ở E. Kẻ EM\(\perp\)AB tại M. Chứng minh rằng:
a, Tam giác BME đồng dạng tam giác AHC
b, Tam giác AEC cân
c, DH.EC=AH.DC
d, AB+AC=BC+DE
cho tam giác ABC vuông tại A, Có góc ABC = \(60^0\). Vẽ AH\(\perp\)BC (H thuộc BC ).
Phân giác của góc HAC cắt BC tại M. MN\(\perp\)AC (N thuộc AC)
a) giả sử AB=3cm, BC=5cm. Tính cạnh AC
b) chứng minh AM là đường trung trực của HN
c) chứng minh tam giác AHN là một tam giác đều
d) đường thẳng HN cắt AB ở D. chứng minh H là trung điểm của ND
a: AC=4cm
b: Xét ΔAMH vuông tại H và ΔAMN vuông tại N có
AM chung
\(\widehat{MAH}=\widehat{NAH}\)
Do đó: ΔAMH=ΔAMN
Suy ra: MH=MN; AH=AN
hay AM là đường trung trực của NH
c: Xét ΔAHN có AH=AN
nên ΔAHN cân tại A
mà \(\widehat{HAN}=60^0\)
nên ΔAHN đều
cho tam giác abc c vuông tại a kẻ ah vuông góc bc tia phân giác của góc hac cắt bc tại d qua d kẻ dk vuông góc ac 1 chứng minh tam giác hac = khd 2 chứng minh tam giác bad cân 3 tia phân giác của bha cắt bc tại e chứng minh ab+ac=bc+de
1: Sửa đề: ΔAHD=ΔAKD
Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
góc HAD=góc KAD
=>ΔAHD=ΔAKD
2: góc BAD+góc CAD=90 độ
góc BDA+góc HAD=90 độ
mà góc CAD=góc HAD
nên góc BAD=góc BDA
=>ΔBAD cân tại B
Cho tam giác ABC vuông tại A, đường phân giác BD. Kẻ \(AE\perp BD\), AE cắt BC tại K
a) Kẻ \(AH\perp BC\). Chứng minh AK là tia phân giác của góc HAC
Xét \(\Delta ABK\)có BE vừa là phân giác vừa là đường cao nên \(\Delta ABK\)cân tại B
\(\Rightarrow\)\(\widehat{BAK}=\widehat{BKA}\)
Ta có :
\(\widehat{BAK}+\widehat{KAC}=90^o\)( 1 )
\(\widehat{AKB}+\widehat{HAK}=90^o\)( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow\)\(\widehat{KAC}=\widehat{HAK}\)( cùng phụ với hai góc bằng nhau )
Từ đó suy ra : AK là tia phân giác của \(\widehat{HAC}\)
Cho tam giác ABC vuông tại A . Phân giác BD , D thuộc AC . Kẻ DE vuông góc BC , E thuộc BC .
a) Chứng minh tam giác ABD = tam giác EBD
b) Kẻ AH vuông góc BC tại H , H thuộc BC . AH cắt BD tại I . Chứng minh AH // DE và tam giác AID cân
c) Chứng minh AE là phân giác của góc HAC
cho tam giác ABC Vuông tại A Kẻ Ah vuông B( H thuộc BC) Tia phân giác góc HAC cách BC tại D chứng minh Tam Giác ABD CÂN
Cho ΔABC vuông tại A (AB < AC)
Kẻ \(AH\perp BC\) tại H
a) Chứng minh \(\widehat{ABC}\) = \(\widehat{HAC}\)
b) Chứng minh \(\widehat{ACB}\) = \(\widehat{HAB}\)
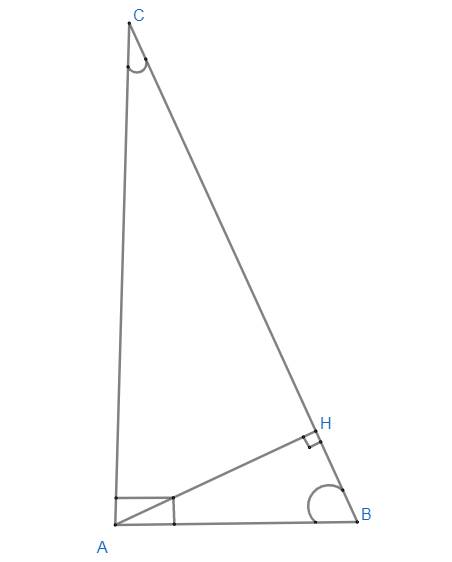
a)
Xét 2 tam giác vuông ABC và HAC có:
\(\widehat{C}\) chung
=> tg ABC \(\sim\) td HAC (g.g)
=> \(\widehat{ABC}=\widehat{HAC}\)
b)
Xét 2 tg vuông ACB và HAB có:
\(\widehat{B}\) chung
=> tg ACB \(\sim\) tg HAB (g.g)
=> \(\widehat{ACB}=\widehat{HAB}\)