(C) tâm I (-3;1) và tiếp xúc với đường thẳng d 3x-4y+1=0

Những câu hỏi liên quan
Viết phương trình của đường tròn (C) trong mỗi trường hợp sau:
a) Có tâm I(-2; 5) và bán kính R= 7;
b) Có tâm I(1;-2) và đi qua điểm A(-2, 2);
c) Có đường kính AB, với A(-1; -3), B(-3; 5);
d) Có tâm I(1; 3) và tiếp xúc với đường thẳng x+2y +3 = 0.
a) Phương trình đường tròn \(\left( C \right)\) là: \({\left( {x + 2} \right)^2} + {\left( {y - 5} \right)^2} = 49\).
b) Bán kính đường tròn là: \(R = IA = \sqrt {{{\left( { - 2 - 1} \right)}^2} + {{\left( {2 - \left( { - 2} \right)} \right)}^2}} = 5\)
Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 25\)
c) Gọi \(I\left( {a;b} \right)\) là trung điểm AB. Vậy tọa độ điểm I là: \(I\left( { - 2;1} \right)\)
Bán kính đường tròn là: \[R = IA = \sqrt {{{\left( { - 1 + 2} \right)}^2} + {{\left( { - 3 - 1} \right)}^2}} = \sqrt {17} \]
Phương trình đường tròn là: \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = 17\)
d) Bán kính đường tròn là: \(R = \frac{{\left| {1 + 2.3 + 3} \right|}}{{\sqrt {{1^2} + {2^2}} }} = 2\sqrt 5 \)
Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 20\)
Đúng 0
Bình luận (0)
Cho đường tròn tâm O, bán kính R, đường kính AB, vẽ đường tròn tâm I, đường kính OA. a. Chm 2 đường tròn tâm O và tâm I tiếp xúc nhau, b. Dây AC của đường tròn tâm O cắt tâm I tại D. Chm ID//OC. c. Biết AC = R căn 3 . Tính theo R , diện tích ODCB
a:
I nằm giữa O và A
=>OI+IA=OA
=>OI=OA-AI
=R-R'
=>(O) với (I) tiếp xúc nhau tại A
b: ΔIAD cân tại I
=>góc IAD=góc IDA
=>góc IDA=góc OAC
ΔOAC cân tại O
=>góc OAC=góc OCA
=>góc IDA=góc OCA
mà hai góc này đồng vị
nên ID//OC
c: Xét (I) có
ΔADO nội tiếp
AO là đường kính
=>ΔADO vuông tại D
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó; ΔACB vuông tại C
Xét ΔACB vuông tại C có cos CAB=AC/AB=1/2*căn 3
=>góc CAB=30 độ
CB=căn AB^2-AC^2=R/2
\(S_{CAB}=\dfrac{1}{2}\cdot CA\cdot CB=\dfrac{1}{2}\cdot\dfrac{R\sqrt{3}}{2}\cdot\dfrac{1}{2}R=\dfrac{R^2\sqrt{3}}{8}\)
Xét ΔADO vuông tại D và ΔACB vuông tại C có
góc DAO chung
Do đó: ΔADO đồng dạng với ΔACB
=>\(\dfrac{S_{ADO}}{S_{ACB}}=\left(\dfrac{AO}{AB}\right)^2=\left(\dfrac{1}{4}\right)\)
=>\(S_{ODCB}=\dfrac{3}{4}\cdot S_{ACB}=\dfrac{3}{4}\cdot\dfrac{R^2\sqrt{3}}{8}=\dfrac{3\cdot\sqrt{3}\cdot R^2}{32}\)
Đúng 0
Bình luận (0)
Lập phương trình đường tròn (C) trong mỗi trường hợp sau:a) (C) có tâm Ileft( { - 4;2} right) và bán kính R 3b) left( C right) có tâm Pleft( {3; - 2} right) và đi qua điểm Eleft( {1;4} right)c) left( C right)có tâm Qleft( {5; - 1} right) và tiếp xúc với đường thẳng Delta :3x + 4y - 1 0d) left( C right) đi qua ba điểm Aleft( { - 3;2} right),Bleft( { - 2; - 5} right),Dleft( {5;2} right)
Đọc tiếp
Lập phương trình đường tròn (C) trong mỗi trường hợp sau:
a) (C) có tâm \(I\left( { - 4;2} \right)\) và bán kính \(R = 3\)
b) \(\left( C \right)\) có tâm \(P\left( {3; - 2} \right)\) và đi qua điểm \(E\left( {1;4} \right)\)
c) \(\left( C \right)\)có tâm \(Q\left( {5; - 1} \right)\) và tiếp xúc với đường thẳng \(\Delta :3x + 4y - 1 = 0\)
d) \(\left( C \right)\) đi qua ba điểm \(A\left( { - 3;2} \right),B\left( { - 2; - 5} \right),D\left( {5;2} \right)\)
a) Phương trình đường tròn (C) có tâm \(I\left( { - 4;2} \right)\) và bán kính \(R = 3\) là: \({\left( {x + 4} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
b) Bán kính đường tròn là: \(R = PE = \sqrt {{{\left( {1 - 3} \right)}^2} + {{\left( {4 + 2} \right)}^2}} = \sqrt {40} \)
Phương trình đường tròn là: \({\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} = 40\).
c) Bán kính đường tròn là: \(R = \frac{{\left| {3.5 + 4.\left( { - 1} \right) - 1} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{{10}}{5} = 2\)
Phương trình đường tròn là: \({\left( {x - 5} \right)^2} + {\left( {y + 1} \right)^2} = 4\)
d) Giả sử tâm đường tròn là điểm \(I\left( {a;b} \right)\). Ta có: \(IA = IB = ID \Leftrightarrow I{A^2} = I{B^2} = I{D^2}\)
Vì \(I{A^2} = I{B^2},I{B^2} = I{D^2}\) nên: \(\left\{ \begin{array}{l}{\left( { - 3 - a} \right)^2} + {\left( {2 - b} \right)^2} = {\left( { - 2 - a} \right)^2} + {\left( { - 5 - b} \right)^2}\\{\left( { - 2 - a} \right)^2} + {\left( { - 5 - b} \right)^2} = {\left( {5 - a} \right)^2} + {\left( {2 - b} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 1\end{array} \right.\)
=> \(I\left( {1; - 1} \right)\) và \(R = IA = \sqrt {{{\left( 4 \right)}^2} + {{\left( { - 3} \right)}^2}} = 5\)
Vậy phương trình đường tròn đi qua 3 điểm A,B, D là: \({\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} = 25\)
Đúng 0
Bình luận (0)
Lập phương trình đường tròn (C) trong các trường hợp sau:
a, (C) có tâm I(-2; 3) và đi qua M(2; -3);
b, (C) có tâm I(-1; 2) và tiếp xúc với đường thẳng x – 2y +7 =0
c, (C) có đường kính AB với A = (1; 1) và B = (7; 5).
a) (C) có tâm I và đi qua M nên bán kính R = IM
Ta có: 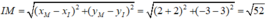
Vậy đường tròn (C) : (x + 2)2 + (y – 3)2 = 52.
b) (C) tiếp xúc với (Δ) : x – 2y + 7 = 0
⇒ d(I; Δ) = R
Mà 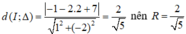
Vậy đường tròn (C) : 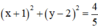
c) (C) có đường kính AB nên (C) có :
+ tâm I là trung điểm của AB
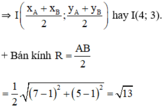
Vậy đường tròn (C) : (x – 4)2 + (y – 3)2 = 13.
Đúng 1
Bình luận (0)
cho tam giác ABC biết A(3 -7) trực tâm H(3 -1) tâm đường tròn ngoại tiếp là I(-2;0). tìm tọa độ C biết C có hoành độ dương
gọi M là giao điểm của AH và đường tròn ngoại tiếp tam giác ABC
Phương trình đường tròn ngoại tiếp tam giác ABC là: \(\left(x+2\right)^2+y^2=74\)
Phương trình đường thẳng AH là : \(x=3\Rightarrow M\left(3;7\right)\)
gọi N là trung điểm của HM \(\Rightarrow N\left(3;3\right)\)
Vẽ hình và chứng minh được H và M đối xứng qua BC
\(\Rightarrow N\in BC\)
Đường thẳng BC qua N và nhận \(\overrightarrow{u_{BC}}\) làm VTPT nên có phương trình là y=3
từ đó tìm được \(c\left(\sqrt{65}-2;3\right)\)
Đúng 0
Bình luận (0)
gọi M là giao điểm của AH và đường tròn ngoại tiếp tam giác ABC
Phương trình đường tròn ngoại tiếp tam giác ABC là: (x+2)2+y2=74(x+2)2+y2=74
Phương trình đường thẳng AH là : x=3⇒M(3;7)x=3⇒M(3;7)
gọi N là trung điểm của HM ⇒N(3;3)⇒N(3;3)
Vẽ hình và chứng minh được H và M đối xứng qua BC
⇒N∈BC⇒N∈BC
Đường thẳng BC qua N và nhận uBC−→−uBC→ làm VTPT nên có phương trình là y=3
từ đó tìm được c(65−−√−2;3)
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho
∆
A
B
C
có đỉnh A ( 3;-7 ), trực tâm H ( 3;-1 ), tâm đường tròn ngoại tiếp I ( -2;0 ). Xác định tung độ đỉnh C A.
y
C
1 B.
y
C
3 C.
y
C
-3 D.
y
C
-1
Đọc tiếp
Trong mặt phẳng Oxy, cho ∆ A B C có đỉnh A ( 3;-7 ), trực tâm H ( 3;-1 ), tâm đường tròn ngoại tiếp I ( -2;0 ). Xác định tung độ đỉnh C
A. y C = 1
B. y C = 3
C. y C = -3
D. y C = -1
Gọi B’ là điểm đối xứng với B qua điểm I. Rõ ràng tứ giác AHCB’ là hình bình hành, cho nên B ' C = A H , tức là C = T A H B '
Do B ' ∈ y là đường tròn ngoại tiếp ∆ A B C nên B = ( y' ) = T A H y ⇒ C = y ∩ y '
Dễ dàng lập được phương trình của các đường tròn (y) và (y') lần lượt như sau
x + 2 2 + y 2 = 74 x + 2 2 + y + 6 2 = 74
Tọa độ điểm C là nghiệm của hệ phương trình
x + 2 2 + y 2 = 74 x + 2 2 + y + 6 2 = 74 ⇒ x = - ± 65 y = - 3
Do đó y C = -3
Đáp án C
Đúng 0
Bình luận (1)
Trong mp Oxy, cho đường tròn (C) có tâm I(–3;−2) , bán kính R 2. Ảnh của đường tròn (C) qua phép quay tâm O góc quay 180
°
là: A.
x
−
3
2
+
y
−
2
2
9
B.
x
+
2...
Đọc tiếp
Trong mp Oxy, cho đường tròn (C) có tâm I(–3;−2) , bán kính R = 2. Ảnh của đường tròn (C) qua phép quay tâm O góc quay 180 ° là:
A. x − 3 2 + y − 2 2 = 9
B. x + 2 2 + y + 3 2 = 9
C. x + 3 2 + y + 2 2 = 9
D. x − 2 2 + y − 3 2 = 9
Đáp án A
Q ( O ; 180 o ) : I → I ' (3;2), bán kính 2
Đúng 0
Bình luận (0)
Lập phương trình đường tròn trong các trường hợp sau:
a) \((C)\) có tâm \(I(1;5)\) và bán kính \(r = 4\)
b) \((C)\) có đường kính MN với \(M(3; - 1)\)và \(N(9;3)\)
c) \((C)\) có tâm \(I(2;1)\) và tiếp xúc với đường thẳng \(5x - 12y + 12 = 0\)
d) \((C)\) có tâm \(A(1; - 2)\) và đi qua điểm \(B(4; - 5)\)
a) Đường tròn (C) tâm \(I(1;5)\), bán kính \(r = 4\) có phương trình là: \({\left( {x - 1} \right)^2} + {\left( {y - 5} \right)^2} = 16\)
b) \(MN = \sqrt {{{\left( {9 - 3} \right)}^2} + {{\left( {3 - ( - 1)} \right)}^2}} = 2\sqrt {13} \), suy ra bán kính là \(\sqrt {13} \)
Tâm của đường tròn là trung điểm của MN: \(I(6;1)\)
Đường tròn (C) tâm \(I\left( {6;1} \right)\)và bán kính là \(\sqrt {13} \) có phương trình: \({\left( {x - 6} \right)^2} + {\left( {y - 1} \right)^2} = 13\)
c) Ta có bán kính của đường tròn \(r = d\left( {I,d} \right) = \frac{{\left| {5.2 - 12.1 + 11} \right|}}{{\sqrt {{5^2} + {{12}^2}} }} = \frac{9}{{13}}\)
Đường tròn (C) tâm \(I\left( {2;1} \right)\)và bán kính là \(\frac{9}{{13}}\) có phương trình: \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{81}}{{169}}\)
d) Bán kính của đường tròn là \(r = AB = \sqrt {{{\left( {4 - 1} \right)}^2} + {{\left( {( - 5) - ( - 2)} \right)}^2}} = 3\sqrt 2 \)
Đường tròn (C) tâm \(A(1; - 2)\)và bán kính là \(3\sqrt 2 \) có phương trình: \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 18\)
Đúng 0
Bình luận (0)
Đường thẳng d: x.cosa + y.sina + 2sina - 3 cos a + 4 = 0 luôn tiếp xúc với đường tròn nào sao đây.
A. Tâm I(3;-2) và R = 4
B. Tâm I(-3;2) và R = 4
C. Tâm I(0;0) và R = 1
D. Tâm I(-3;-2) và R = 4
Giả sử đường tròn cố định là d tiếp xúc có tâm \(I\left(x;y\right)\) và bán kính R
\(\Rightarrow d\left(I;d\right)=R\) với mọi a
\(\Rightarrow\dfrac{\left|x.cosa+y.sina+2sina-3cosa+4\right|}{\sqrt{cos^2a+sin^2a}}=R\)
\(\Leftrightarrow\left|\left(x-3\right)cosa+\left(y+2\right)sina+4\right|=R\)
Đẳng thức đúng với mọi a khi và chỉ khi:
\(\left\{{}\begin{matrix}x-3=0\\y+2=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\) \(\Rightarrow I\left(3;-2\right)\) và \(R=4\)
Đúng 2
Bình luận (5)
4. Trong mặt phẳng Oxy, cho đường thẳng d: x − 3y + 1 = 0 và điểm I(−3; 1).
(a) Tìm ảnh của điểm M(1; −2) qua phép đối xứng tâm I.
(b) Tìm ảnh của đường thẳng ∆: 2x + y − 1 = 0 qua phép đối xứng tâm I.
(c) Tìm ảnh của đường tròn (C): (x − 2)2 + (y + 3)2 = 9 qua phép đối xứng














