đỉnh của tam giác vuông abc là A(0;1) cạnh đáy BC nằm trên đường thẳng x+2y+3=0. Viết phương trình 2 cạnh AB, AC

Những câu hỏi liên quan
cho tam giác ABC nội tiếp đường tròn tâm I, có đỉnh A thuộc đường thẳng d:x+y-2=0, điểm D(-2;1) là chân đường cao của tam giác ABC hạ từ A. Gọi E(3;1) là chân đường vuông góc hạ từ B xuống AI, điểm P(2;1) thuộc cạnh AC. Tìm tọa độ các đỉnh của tam giác ABC
Ta dễ có tứ giác ABDE nội tiếp đường tròn đường kính AB => ^CDE = ^BAE
Lại có ^BAE = ^CAD (= 900 - ^ACB), suy ra ^CDE = ^CAD = 900 - ^ACD => DE vuông góc AC
Thấy D,E,P cùng có tung độ bằng 1 => D,E,P thẳng hàng, vì P thuộc AC nên DE vuông góc với AC tại P
Đường thẳng AC: đi qua P(2;1), VTPT \(\overrightarrow{DE}=\left(5;0\right)\) \(\Rightarrow AC:x-2=0\)
Xét hệ: \(\hept{\begin{cases}x-2=0\\x+y-2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=0\end{cases}}\Rightarrow A\left(2;0\right)\)
Đường thẳng BC: đi qua \(D\left(-2;1\right)\),VTPT \(\overrightarrow{DA}=\left(4;-1\right)\Rightarrow BC:4x-y+9=0\)
Xét hệ: \(\hept{\begin{cases}x-2=0\\4x-y+9=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=17\end{cases}\Rightarrow C\left(2;17\right)}\)
Đường thẳng BE: đi qua \(E\left(3;1\right)\), VTPT \(\overrightarrow{AE}=\left(1;1\right)\Rightarrow BE:x+y-4=0\)
Xét hệ: \(\hept{\begin{cases}4x-y+9=0\\x+y-4=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-1\\y=5\end{cases}}\Rightarrow B\left(-1;5\right)\)
Vậy \(A\left(2;0\right),B\left(-1;5\right),C\left(2;17\right)\).
Trong mặt phẳng với hệ tọa độ Oxy Cho tam giác ABC nội tiếp trong đường tròn tâm I; có đỉnh A thuộc đường thẳng d: x + y - 2 = 0, D(2; -1) là chân đường cao của tam giác ABC hạ từ đỉnh A. Gọi điểm E(3; 1) là chân đường vuông góc hạ từ B xuống AI; điểm P(2;1) thuộc đường thẳng AC. Tìm tọa độ các đỉnh của tam giác ABC.
MAT DAY LOP 6,7,8,9 MA DUA LOP 1 , MAT DAY DI MA
Đúng 0
Bình luận (0)
1/cho tam giác abc , bên ngoài tam giác vẽ 2 hình vuông abef và acgh ,
a/CM: đường cao từ đỉnh A của tam giác ABC là đường trung tuyến của tam giác tam giác AHF
b/CM: đường trung tuyến từ đỉnh A của tam giác ABC là đường cao của tam giác AHF
cho tam giác ABC nội tiếp đường tròn tâm I, có đỉnh A thuộc đường thẳng d:x+y-2=0, điểm D(-2;1) là chân đường cao của tam giác ABC hạ từ A. Gọi E(3;1) là chân đường vuông góc hạ từ B xuống AI, điểm P(2;1) thuộc cạnh AC. Tìm tọa độ các đỉnh của tam giác ABC
Cho tam giác ABC có goác A < 900. Vẽ ngoài tam giác ABC các tam giác vuông cân đỉnh A là MAB, NAC
a, CM : MC=NB
b, CM : MC vuông góc với NB
cho đỉnh của tam giác vuông cân ABC là A(1;4), cạnh đáy BC nằm trên 3x-2y-1=0.viết pt AB,AC
Cho tam giác ABC có góc A<900. Trên nửa mp chứa đỉnh C bờ là đường thẳng AB vẽ AE vuông góc AB và đặt AE=AB. Trên nửa mp ko chứa đỉnh B bờ là đường thẳng AC vẽ tia AD vuông góc AC và AD=AC. Nối E vs D. M,Nlaf các trđiểm của BC và ED. CMR:
a) tam giác ABC=tam giác AED
b) Tam giác AMC=tam giác AND
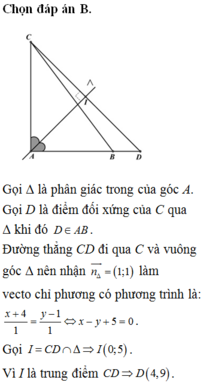
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại A và có đỉnh C(-4;1). Đường phân giác trong góc A có phương trình là x+y-50. Biết diện tích tam giác ABC bằng 24 và đỉnh A có hoành độ dương. Tìm tọa độ điểm B. A. B(4;-5) B. B(4;7) C. B(4;5) D. B(4;-7)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại A và có đỉnh C(-4;1). Đường phân giác trong góc A có phương trình là x+y-5=0. Biết diện tích tam giác ABC bằng 24 và đỉnh A có hoành độ dương. Tìm tọa độ điểm B.
A. B(4;-5)
B. B(4;7)
C. B(4;5)
D. B(4;-7)
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại A và có đỉnh C(-4;1). Đường phân giác trong góc A có phương trình là x+y-50. Biết diện tích tam giác ABC bằng 24 và đỉnh A có hoành độ dương. Tìm tọa độ điểm B.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại A và có đỉnh C(-4;1). Đường phân giác trong góc A có phương trình là x+y-5=0. Biết diện tích tam giác ABC bằng 24 và đỉnh A có hoành độ dương. Tìm tọa độ điểm B.
![]()
![]()
![]()
![]()
cho tam giác ABC vuông tại A biết B^ = 70° tính được góc ngoài của tam giác ABC tại đỉnh C là
có : ( tổng ba góc của một tam giác )
Mà ( hai góc kề bù )
Đúng 0
Bình luận (0)