a.

\(\overrightarrow{BA}=\left(4;7\right)\Rightarrow\) đường thẳng AB nhận (4;7) là 1 vtcp

Phương trình tham số AB: \(\left\{{}\begin{matrix}x=3+4t\\y=2+7t\end{matrix}\right.\)

b.

\(\overrightarrow{AB}=\left(4;-7\right)\) \(\Rightarrow\) đường thẳng AB nhận (4;-7) là 1 vtcp

Phương trình AB: \(\left\{{}\begin{matrix}x=-3+4t\\y=1-7t\end{matrix}\right.\)

\(A\left(\sqrt{3}-\sqrt{2};1-\sqrt{6}\right)\in\left(d\right)\\ \Leftrightarrow\left(\sqrt{3}-\sqrt{2}\right)a+b=1-\sqrt{6}\left(1\right)B\left(\sqrt{2};2\right)\in\left(d\right)\\ \Leftrightarrow a\sqrt{2}+b=2\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}a\sqrt{3}-a\sqrt{2}+b=1-\sqrt{6}\\a\sqrt{2}+b=2\end{matrix}\right.\)

Lấy 2 PT trừ nhau

\(\Leftrightarrow a\left(2\sqrt{2}-\sqrt{3}\right)=1+\sqrt{6}\\ \Leftrightarrow a=\dfrac{\sqrt{6}+1}{2\sqrt{2}-\sqrt{3}}=\dfrac{\left(\sqrt{6}+1\right)\left(2\sqrt{2}+\sqrt{3}\right)}{8-3}\\ \Leftrightarrow a=\dfrac{11\sqrt{2}+\sqrt{3}}{5}\\ \Leftrightarrow b=2-a\sqrt{2}=\dfrac{10-\sqrt{2}\left(11\sqrt{2}+\sqrt{3}\right)}{5}\\ \Leftrightarrow b=\dfrac{-12-\sqrt{6}}{5}\)

Tham khảo:

a) Ta có: \(\overrightarrow b  = \left( {4; - 1} \right)\) và \(\overrightarrow a  = 3.\overrightarrow i  - 2.\overrightarrow j \;\; \Rightarrow \;\overrightarrow a \;\left( {3; - 2} \right)\)

\( \Rightarrow 2\;\overrightarrow a  - \overrightarrow b  = \left( {2.3 - 4\;;\;2.\left( { - 2} \right) - \left( { - 1} \right)} \right) = \left( {2; - 3} \right)\)

Lại có: M (-3; 6), N(3; -3)

\( \Rightarrow \overrightarrow {MN}  = \left( {3 - \left( { - 3} \right); - 3 - 6} \right) = \left( {6; - 9} \right)\)

Dễ thấy:\(\left( {6; - 9} \right) = 3.\left( {2; - 3} \right)\) \( \Rightarrow \overrightarrow {MN}  = 3\left( {2\;\overrightarrow a  - \overrightarrow b } \right)\)

b) Ta có: \(\overrightarrow {OM}  = \left( { - 3;6} \right)\) ( do M(-3; 6)) và \(\overrightarrow {ON}  = \left( {3; - 3} \right)\) (do N (3; -3)).

Hai vectơ này không cùng phương (vì \(\frac{{ - 3}}{3} \ne \frac{6}{{ - 3}}\)).

Do đó các điểm O, M, N không cùng nằm trên một đường thẳng.

Vậy chúng không thẳng hàng.

c) Các điểm O, M, N không thẳng hàng nên OMNP là một hình hành khi và chỉ khi \(\overrightarrow {OM}  = \overrightarrow {PN} \).

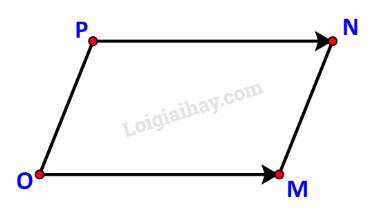
Do \(\overrightarrow {OM}  = \left( { - 3;6} \right),\;\overrightarrow {PN}  = \left( {3 - x; - 3 - y} \right)\)  nên

\(\overrightarrow {OM}  = \overrightarrow {PN}  \Leftrightarrow \left\{ \begin{array}{l} - 3 = 3 - x\\6 =  - 3 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y =  - 9\end{array} \right.\)

Vậy điểm cần tìm là P (6; -9).

Đáp án đúng là D

+ Xét điểm \(\left( {1;1} \right)\) ta có: \(y =  - 5.1 + 5 = 0 \ne 1\). Do đó, điểm \(\left( {1;1} \right)\)không thuộc đồ thị hàm số.

+ Xét điểm \(\left( {2;0} \right)\) ta có: \(y =  - 5.2 + 5 =  - 5 \ne 0\). Do đó, điểm \(\left( {2;0} \right)\)không thuộc đồ thị hàm số.

+ Xét điểm \(\left( {0;4} \right)\) ta có: \(y =  - 5.0 + 5 = 5 \ne 4\). Do đó, điểm \(\left( {0;4} \right)\)không thuộc đồ thị hàm số.

+ Xét điểm \(\left( {2; - 5} \right)\) ta có: \(y =  - 5.2 + 5 =  - 5\). Do đó, điểm \(\left( {2; - 5} \right)\) thuộc đồ thị hàm số.

Đáp án đúng là D

+ Xét điểm \(\left( {1;1} \right)\) ta có: \(y = 2 - 4.1 =  - 2 \ne 1\). Do đó, điểm \(\left( {1;1} \right)\)không thuộc đồ thị hàm số.

+ Xét điểm \(\left( {2;0} \right)\) ta có: \(y = 2 - 4.2 =  - 6 \ne 2\). Do đó, điểm \(\left( {2;0} \right)\)không thuộc đồ thị hàm số.

+ Xét điểm \(\left( {1; - 1} \right)\) ta có: \(y = 2 - 4.1 =  - 2 \ne  - 1\). Do đó, điểm \(\left( {1; - 1} \right)\)không thuộc đồ thị hàm số.

+ Xét điểm \(\left( {1; - 2} \right)\) ta có: \(y = 2 - 4.1 =  - 2\). Do đó, điểm \(\left( {1; - 2} \right)\) thuộc đồ thị hàm số.

Thế lần lượt chọn ý D

Bài 2:

Ta có : 1/a-1/b=b-a/a.b

suy ra:b-a=2

và:b.a=143

Vì b-a=2 nên suy ra a và b là 2 số chẵn hoặc lẻ liên tiếp mà chẵn nhân chẵn luôn bằng chẵn;lẻ nhân lẻ luôn bằng lẻ. Vậy a và b là hai số lẻ liên tiếp.

Ta có:143=1.143 (loại)

              =11.13 (phù hợp)

Vậy:a=11;b=3

a) 

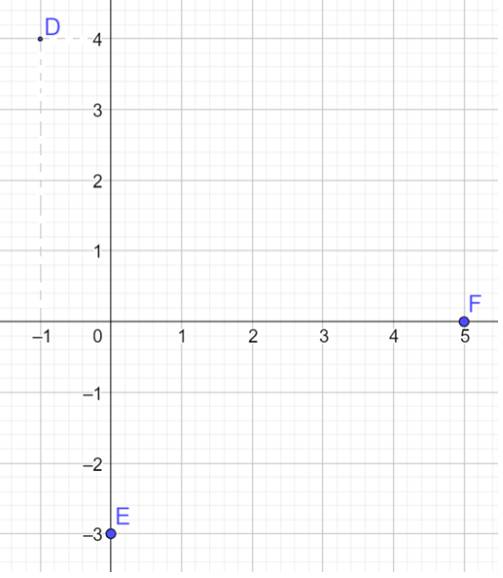
b) Vì tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ của điểm M (với mọi M) nên ta có:

\(\overrightarrow {OD}  = \left( { - 1;4} \right),\overrightarrow {OE}  = \left( {0; - 3} \right),\overrightarrow {OF}  = \left( {5;0} \right)\)

c) 

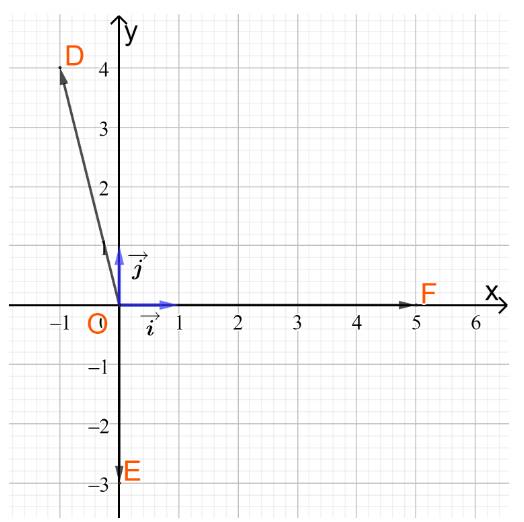
Từ hình vẽ ta có tọa độ của hai vectơ   và \(\overrightarrow j \)là

 và \(\overrightarrow j  = (0;1)\)

a: (d): y=ax+b

Theo đề, ta có hệ:

a+b=3 và 2a+b=4

=>a=1 và b=2

b: Theo đề, ta có hệ:

-3a+b=2 và 2a+b=3

=>a=1/5 và b=13/5