Đường thẳng ax+by-6=0 tạo với tia Ox 1 góc 30o và cách gốc toạ độ O(0;0) 1 khoảng bằng 3. Giá trị của biểu thức T=a^2+b^2 là

Những câu hỏi liên quan
mọi người giúp mình với ạ
đường thẳng ax+by-6=0 tạo với trục ox một góc 30 độ và cách gốc toạ độ O(0;0) một khoảng =3 tính giá trị biểu thức T=a^2+b^2
Trên mặt phẳng toạ độ cho đường thẳng (d) có phương trình: 2kx + (k – 1)y = 2 (k là tham số)
1. Tìm k để đường thẳng (d) song song với đường thẳng y = ? Khi đó hãy tính góc tạo bởi (d) và tia Ox.
2. Tìm k để khoảng cách từ gốc toạ độ đến đường thẳng (d) là lớn nhất?
Trên mặt phẳng toạ độ cho đường thẳng (d) có phương trình: 2kx + (k – 1)y = 2 (k là tham số)
1. Tìm k để đường thẳng (d) song song với đường thẳng y = ? Khi đó hãy tính góc tạo bởi (d) và tia Ox.
2. Tìm k để khoảng cách từ gốc toạ độ đến đường thẳng (d) là lớn nhất?
CHo hàm số y = ax + b
Xác định hàm số biết đồ thị của nó đi qua gốc toạ độ và P(\((\sqrt{3};1)\). Khi đó tính góc tạo bởi đường thẳng này với trục Ox
- Gọi phương trình đường thẳng cần tìm có dạng : y = ax + b
- Thay tọa độ của điểm O và P và hàm số ta được hệ :
\(\left\{{}\begin{matrix}0a+b=0\\a\sqrt{3}+b=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=0\\a=\dfrac{\sqrt{3}}{3}\end{matrix}\right.\)
=> Phương trình đường thẳng là : \(y=\dfrac{\sqrt{3}}{3}x\)
\(\Rightarrow Tan\alpha=a=\dfrac{\sqrt{3}}{3}\)
\(\Rightarrow\alpha=30^o\)
Vậy ...
Đúng 3
Bình luận (0)
Cho đường thẳng d có phương trình tổng quát là: x - 2y – 5 = 0.
a) Lập phương trình tham số của đường thẳng d.
b) Tìm toạ độ điểm M thuộc d sao cho OM = 5 với O là gốc toạ độ.
c) Tìm toạ độ điểm N thuộc d sao cho khoảng cách từ N đến trục hoành Ox là 3.
a) Từ phương trình tổng quát của đường thẳng, ta lấy được một vecto pháp tuyến là: \(\overrightarrow n = \left( {1; - 2} \right)\) nên ta chọn vecto chỉ phương của đường thẳng d là: \(\overrightarrow u = \left( {2;1} \right)\).
Chọn điểm \(A\left( {1; - 2} \right) \in d\).Vậy phương trình tham số của đường thẳng d là: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = - 2 + t\end{array} \right.\) (t là tham số)
b) Do điểm M thuộc d nên ta có: \(M\left( {1 + 2m; - 2 + m} \right);m \in \mathbb{R}\).
Ta có: \(OM = 5 \Leftrightarrow \sqrt {{{\left( {1 + 2m} \right)}^2} + {{\left( { - 2 + m} \right)}^2}} = 5 \Leftrightarrow {m^2} = 4 \Leftrightarrow m = \pm 2\)
Với \(m = 2 \Rightarrow M\left( {5;0} \right)\)
Với \(m = - 2 \Rightarrow M\left( { - 3; - 4} \right)\)
Vậy ta có 2 điểm M thỏa mãn điều kiện đề bài.
c) Do điểm N thuộc d nên ta có: \(N\left( {1 + 2n; - 2 + n} \right)\)
Khoảng cách từ N đến trục hoành bằng giá trị tuyệt đối của tung độ điểm N. Do đó, khoảng cách tư N đến trục hoành bằng 3 khi và chỉ khi: \(\left| { - 2 + n} \right| = 3 \Leftrightarrow \left[ \begin{array}{l}n = 5\\n = - 1\end{array} \right.\)
Với \(n = 5 \Rightarrow N\left( {11;3} \right)\)
Với \(n = - 1 \Rightarrow N\left( { - 1; - 3} \right)\)
Vậy có 2 điểm N thỏa mãn bài toán
Đúng 0
Bình luận (0)
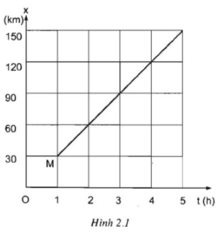
Hình 2.1 là đồ thị toạ độ - thời gian của môt chiếc ô tô chay từ A đến B trên một đường thẳng. Điểm A cách gốc toạ độ bao nhiêu kilômét ? Thời điểm xuất phát cách mốc thời gian mấy giờ ?A. A trùng với gốc toạ độ o, xe xuất phát lúc 0 h, tính từ mốc thời gian.B. A trùng với gốc toạ độ o, xe xuất phát lúc 1 h, tính từ mốc thời gian.C. A cách gốc o 30 km, xe xuất phát lúc 0 h.D. A cách gốc o 30 km, xe xuất phát lúc 1 h.
Đọc tiếp
Hình 2.1 là đồ thị toạ độ - thời gian của môt chiếc ô tô chay từ A đến B trên một đường thẳng. Điểm A cách gốc toạ độ bao nhiêu kilômét ? Thời điểm xuất phát cách mốc thời gian mấy giờ ?
A. A trùng với gốc toạ độ o, xe xuất phát lúc 0 h, tính từ mốc thời gian.
B. A trùng với gốc toạ độ o, xe xuất phát lúc 1 h, tính từ mốc thời gian.
C. A cách gốc o 30 km, xe xuất phát lúc 0 h.
D. A cách gốc o 30 km, xe xuất phát lúc 1 h.
Cho hàm số : 1, y=2x-1 2, y= -3x+2 3, y=3x+4 4, y= -1/3x +2 5, y=2/3x +2
1. Vẽ đồ thị hàm số
2. Tính góc tạo bởi đường thẳng đó với trục Ox
3.Đường thẳng cắt trục Ox và Oy lần lượt tại A,B. Tính diện tích tam giác AOB
4. Tìm khoảng cách từ gốc toạ độ đến đường thẳng đó
5. Tìm toạ độ giao điểm của các hàm số trên với trục tung và trục hoành
viết công thức đường thẳng yax+byax+ba) đi qua M(1;2) song song y2x−100y2x−100b) đi qua k(-1;8) song song với trục Oxc) cắt Oy tại điểm có tung độ y -1 song song với đường phân giác của góc vuông thứ 2d) đi qua gốc toạ độ và hợp với chiều dương của Ox 1 góc 45o
Đọc tiếp
viết công thức đường thẳng
a) đi qua M(1;2) song song
b) đi qua k(-1;8) song song với trục Ox
c) cắt Oy tại điểm có tung độ y = -1 song song với đường phân giác của góc vuông thứ 2
d) đi qua gốc toạ độ và hợp với chiều dương của Ox 1 góc 45o
a: Vì (d)//y=2x-100 nên a=2
=>y=2x+b
Thay x=1 và y=2 vào (d),ta được:
b+2=2
=>b=0
b: Vì (d)//Ox nên y=b
Thay x=-1 và y=8 vào (d), ta được:
0*(-1)+b=8
=>y=8
d: a=tan alpha=1
=>y=x+b
Thay x=0 và y=0 vào(d), ta được:
b+0=0
=>b=0
Đúng 0
Bình luận (0)
Biết rằng đường thẳng d1: ax+by-3=0 tạo với đường thẳng d2:3x-y+7=0 một góc 45 độ và a,b là số nguyên. Tính giá trị biểu thức a-b



















