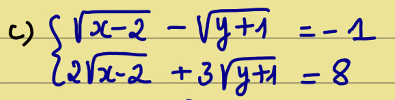
ĐKXĐ:\(\left\{{}\begin{matrix}x\ge2\\y\ge-1\end{matrix}\right.\)

\(\left\{{}\begin{matrix}\sqrt{x-2}-\sqrt{y+1}=-1\\2\sqrt{x-2}+3\sqrt{y+1}=8\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3\sqrt{x-2}-3\sqrt{y+1}=-3\\2\sqrt{x-2}+3\sqrt{y+1}=8\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\sqrt{x-2}-\sqrt{y+1}=-1\\5\sqrt{x-2}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}1-\sqrt{y+1}=-1\\\sqrt{x-2}=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\sqrt{y+1}=2\\x-2=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y+1=4\\x=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3\\x=3\left(tm\right)\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}3\sqrt{x-2}-3\sqrt{y+1}=-3\\2\sqrt{x-2}+3\sqrt{y+1}=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5\sqrt{x-2}=5\\\sqrt{x-2}-\sqrt{y+1}=-1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x-2=1\\y+1=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=3\end{matrix}\right.\)

a) m = 3 thì hệ trở thành \(\hept{\begin{cases}3x+y=3\\2x-y=7\end{cases}}\Leftrightarrow\hept{\begin{cases}6x+2y=6\left(1\right)\\6x-3y=21\left(2\right)\end{cases}}\)

\(\left(1\right)-\left(2\right)\Leftrightarrow5y=-15\Leftrightarrow y=-3\)

Từ đó suy ra \(x=2\)

Vậy với m = 3 thì hệ có 1 nghiệm (2;-3)

b) HPT không thể có nghiệm (3;1)

c) HPT có nghiệm (4;1) thì \(4m+1=3\Leftrightarrow m=\frac{1}{2}\)

a/ Xét pt : \(\left\{{}\begin{matrix}mx-y=1\\\dfrac{x}{2}-\dfrac{y}{2}=335\end{matrix}\right.\)

 Khi \(m=2\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x-y=1\\x-y=670\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=-669\\y=-1339\end{matrix}\right.\)

b/ \(\left\{{}\begin{matrix}mx-y=1\\x-y=670\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=x-670\\mx-\left(x-670\right)=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=x-670\\x\left(m-1\right)=-669\end{matrix}\right.\)

Để pt có nghiệm duy nhất \(\Leftrightarrow m\ne1\)

Vậy...

\(\left\{{}\begin{matrix}2x-y=x+3y+3\\3x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+x-y=x+3y+3\\x-y=3\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x+3-x-3y-3=0\\x=3+y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3y=0\\x=3+y\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=3+y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=3+0=3\end{matrix}\right.\)

a: Khi a=1 thì hệ sẽ là:

x-3y=4 và 3x+2y=1

=>x=1; y=-1

b: Để hệ vô nghiệm thì a/3=-3/2<>4/1

=>a=-9/2

1) Cho hệ phương trình:

{mx+y=52x−y=−2(I){mx+y=52x−y=−2(I)

a) Với m=1 ta có hệ phương trình:

{x+y=52x−y=−2{x+y=52x−y=−2

Cộng vế với vế ta được:

3x=3⇔x=1⇒y=2x+2=43x=3⇔x=1⇒y=2x+2=4

Vậy với  m=11m=11 thì hệ phương trình (I) có nghiệm x=1 và y=4

b) Nghiệm (x0,y0)(x0,y0) của  (I) thỏa mãn x0+y0=1x0+y0=1

nên ta có hệ phương trình:

⎧⎪⎨⎪⎩x+y=1(1)mx+y=5(2)2x−y=−2(3){x+y=1(1)mx+y=5(2)2x−y=−2(3)

Lấy (1) + (3) ta được: 3x=−1⇒x=−13⇒y=1−x=433x=−1⇒x=−13⇒y=1−x=43

Thay vào (2) suy ra m=5−yx=−11m=5−yx=−11

Vậy với m=−11m=−11 thì nghiệm của hệ phương trình (I) có tổng là 1.

2) Từ x+my=2⇒x=2−myx+my=2⇒x=2−my

Thay vào phương trình mx−2y=1mx−2y=1 ta được:

m(2−my)−2y=1⇒y=2m−1m2+2m(2−my)−2y=1⇒y=2m−1m2+2

⇒x=2−m2m−1m2+2⇒x=2−m2m−1m2+2

x=m+4m2+2x=m+4m2+2

Do m2+2>0m2+2>0 ∀m∀m

⇒x>0⇒m+4>0⇒m>−4⇒x>0⇒m+4>0⇒m>−4 và y<0⇒2m−1<0⇒m<12y<0⇒2m−1<0⇒m<12

Vậy với −4<m<12−4<m<12 thì phương trình có nghiệm duy nhất mà x>0,y<0

I don't know how to do this