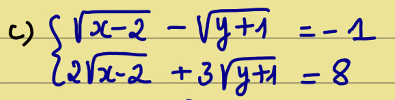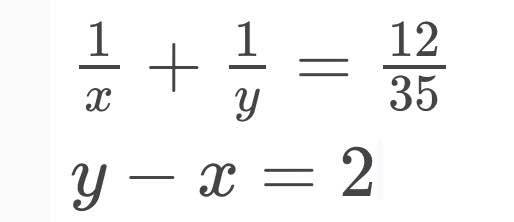ĐKXĐ:\(\left\{{}\begin{matrix}x\ge2\\y\ge-1\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\sqrt{x-2}-\sqrt{y+1}=-1\\2\sqrt{x-2}+3\sqrt{y+1}=8\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3\sqrt{x-2}-3\sqrt{y+1}=-3\\2\sqrt{x-2}+3\sqrt{y+1}=8\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\sqrt{x-2}-\sqrt{y+1}=-1\\5\sqrt{x-2}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}1-\sqrt{y+1}=-1\\\sqrt{x-2}=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\sqrt{y+1}=2\\x-2=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y+1=4\\x=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3\\x=3\left(tm\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3\sqrt{x-2}-3\sqrt{y+1}=-3\\2\sqrt{x-2}+3\sqrt{y+1}=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5\sqrt{x-2}=5\\\sqrt{x-2}-\sqrt{y+1}=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2=1\\y+1=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=3\end{matrix}\right.\)