Theo đề ta có: \(\widehat{BAH}=2\widehat{CAH}\Rightarrow\widehat{A}=3\widehat{CAH}\)

Mà \(\widehat{A}=72^o\left(gt\right)\) \(\Rightarrow3\widehat{CAH}=72^o\)

\(\Rightarrow\widehat{CAH}=24\) \(\Rightarrow BAH=24^o.2=48^o\)

Ta lại có: \(\widehat{B}+\widehat{BAH}=90^o\) (định lí của một tam giác vuông)

hay \(\widehat{B}+48^o=90^o\Rightarrow\widehat{B}=42^o\)

Tương tự: \(\widehat{C}+\widehat{CAH}=90^o\)

hay \(\widehat{C}+24^o=90^o\Rightarrow\widehat{C}=66^o\)

Vậy góc B có số đo là \(42^o\)

góc C có số đo là \(66^o\)

Vì ΔABC vuông tại A

==> BC² = AC² +AB² ( Định lý Pitago )

       BC² = 4² + 3² 

       BC² = 27

==> BC = √27

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=3^2+4^2=25\)

hay BC=5(cm)

Vậy: BC=5cm

b) Xét ΔABC có AC>AB(4cm>3cm)

mà góc đối diện với cạnh AC là \(\widehat{ABC}\)

và góc đối diện với cạnh AB là \(\widehat{ACB}\)

nên \(\widehat{B}>\widehat{C}\)(Định lí quan hệ giữa cạnh và góc đối diện trong tam giác)

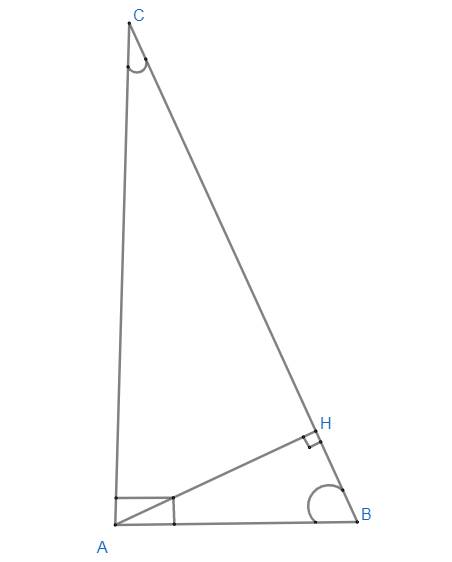
a)

Xét 2 tam giác vuông ABC và HAC có:

\(\widehat{C}\) chung

=> tg ABC \(\sim\) td HAC (g.g)

=> \(\widehat{ABC}=\widehat{HAC}\)

b)

Xét 2 tg vuông ACB và HAB có:

\(\widehat{B}\) chung

=> tg ACB \(\sim\) tg HAB (g.g)

=> \(\widehat{ACB}=\widehat{HAB}\)

a) Xét hai tam giác vuông ABH và ACH

có:+AB=AC( \(\Delta ABC\) cân tại A)

      +AH: cạnh chung

Vậy \(\Delta ABH=\Delta ACH\left(ch-cgv\right)\)

=> HB=HC(  hai cạnh tương ứng)

b) Vì \(\Delta ABH=\Delta ACH\left(cmt\right)\)

nên: góc BAH=góc CAH( hai góc tương ứng)

 ^..^ ^_^

a) Xét \(\Delta\nu ABH\) và \(\Delta\nu ACH\) có :

   \(AB=AC\left(gt\right)\)

   \(AH\) là cạnh chung

 Do đó : \(\Delta\nu ABH=\Delta\nu ACH\left(ch-gn\right)\)

\(\Rightarrow HB=HC\) ( vì hai cạnh tương ứng )

b )  Vì : \(\Delta\nu ABH=\Delta\nu ACH\)

\(\Rightarrow\widehat{BAH}=\widehat{CAH}\)

 

a)Xét tam giác ABH và tam giác ACH,có:

AB=AC(vì tam giác ABC cân tại A)

BAH=CAH=90

AH là cạnh chung.

=>tam giác ABH=tam giác ACH(cạnh huyền-cạnh góc vuông)

=>HB=HC (2 cạnh tương ứng)

b) Vì tam giác ABH=tam giác ACH (C/m trên)

=>góc BAH=góc CAH(2 góc tương ứng)

Ghi nhớ:

_ Nếu 2 cạnh góc vuông của tam giác vuông này lần lượt bằng 2 cạnh góc vuông của tam giác vuông kia thì tam giác vuông đó bằng nhau (theo trường hợp cạnh-góc-cạnh)

_Nếu 1 cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (theo trường hợp góc-cạnh-góc).

_Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (theo trường hợp góc-cạnh-góc).

_Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

a) Hai tam giác vuông ABH và ACH có:

AB=AC(gt)

AH cạnh chung.

Nên ∆ABH=∆ACH(Cạnh huyền-cạnh góc vuông)

Suy ra HB=HC

b)∆ABH=∆ACH(Câu a)

Suy ra ^BAH=^CAH(Hai góc tương ứng)

a) Hai tam giác vuông ABH và ACH có:

AB=AC(gt)

AH cạnh chung.

Nên ∆ABH=∆ACH(Cạnh huyền-cạnh góc vuông)

Suy ra HB=HC

b)∆ABH=∆ACH(Câu a)

Suy ra =(Hai góc tương ứng)

Xem thêm tại: http://loigiaihay.com/bai-63-trang-136-sach-giao-khoa-toan-7-tap-1-c42a5157.html#ixzz4envied4H

a) Hai tam giác vuông ABH và ACH có:

AB=AC(gt)

AH cạnh chung.

Nên ∆ABH=∆ACH(Cạnh huyền-cạnh góc vuông)

Suy ra HB=HC

b)∆ABH=∆ACH(Câu a)

Suy ra =(Hai góc tương ứng)

a) Hai tam giác vuông ABH và ACH có:

AB=AC(gt)

AH cạnh chung.

Nên ∆ABH=∆ACH(Cạnh huyền-cạnh góc vuông)

Suy ra HB=HC

b)∆ABH=∆ACH(cmt)

Suy ra BAH=CAH(Hai góc tương ứng)

a) Xét tam giác AHB và tam giác AHC có:

\(\widehat{AHB}=\widehat{AHC}=90^o\)

AB=AC(tam giác ABC cân)

\(\widehat{ABC}=\widehat{ACB}\)(tam giác ABC cân)

Do đó tam giác AHB=tam giác AHC(ch-gn)

Suy ra HB=HC(hai cạnh tương ứng)

b)Vì tam giác AHB=tám giác AHC(câu a)

Nên \(\widehat{BAH}=\widehat{CAH}\)(hai góc tương ứng)

a, Xét \(\Delta ABC\),ta có:

\(\widehat{A}=90\)

=> \(\widehat{B}+\widehat{C}=90\)       (1)

Xét \(\Delta CAH\),ta có:

\(\widehat{AHC}=90\)

=>\(\widehat{CAH}+\widehat{C}=90\)  (2)

Từ (1) và (2)=>\(\widehat{B}=\widehat{CAH}\)  (đpcm)

b, Xét \(\Delta BAH\),ta có:

\(\widehat{AHB}=90\)

=>\(\widehat{B}+\widehat{BAH}=90\)   (3)

Từ (1) và (3)=>\(\widehat{C}=\widehat{BAH}\)   (đpcm)

a, tam giác AHB vuông tại H (gt) => ^B + ^HAB = 90 (đl)

^BAC = 90 (gt) => ^HAB  + ^CAH = 90 

=> ^B = ^CAH 

b, tương tự a

A) XÉT \(\Delta ABC\)CÓ \(\widehat{B}=90^o-\widehat{C}\left(1\right)\)

XÉT \(\Delta HAC\)CÓ \(\widehat{CAH}=90^o-\widehat{C}\left(2\right)\)

TỪ (1) VÀ (2) => \(\widehat{B}=\widehat{CAH}\left(đpcm\right)\)

b) XÉT \(\Delta ABC\)CÓ \(\widehat{C}=90^o-\widehat{B}\left(1\right)\)

XÉT \(\Delta ABH\)CÓ \(\widehat{BAH}=90^o-\widehat{B}\left(2\right)\)

TỪ (1) VÀ (2) => \(\widehat{C}=\widehat{BAH}\left(đpcm\right)\)

Sửa tam giác ABC cân tại A nhé chứ là tam giác vuông thì chỉ có c.g thôi 

a, Xét tam giác BHA và tam giác AHC ta có : 

AH _ chung 

^BHA = ^AHC = 90⁰

^ABH = ^ACH ( gt ) vì ABC cân tại A

Vậy tam giác BHA = tam giác AHC ( g.c.g )

=> BH = HC ( 2 cạnh tương ứng )

b, Xét tam giác BAH và tam giác CAH ta có : 

BH = HC ( cmt )

^AHB = ^AHC = 90⁰

AH _ chung 

Vậy tam giác BAH = tam giác CAH ( c.g.c )

=> ^BAH = ^CAH ( 2 góc tương ứng )

a) Xét tam giác ABH và tam giác ACH vuông tại H có:

+) AB = AC (chứng minh trên)

+) Góc B = góc C (cmt)

=> Tam giác ABH = tam giác ACH (cạnh huyền - góc nhọn)

=> HB = HC (2 cạnh tương ứng)

b)  Vì tam giác ABH = tam giác ACH nên:

=> Góc BAH = góc CAH (2 góc tương ứng)

Chứng minh:

a, Xét \(\Delta ABH\) và \(\Delta ACH\), có:

\(\)AB=AC (tam giác ABC cân tại A) -> cạnh huyền

AH: cạnh chung -> cạnh góc vuông

\(\widehat{AHB}=\widehat{AHC}->gócvuông\)

=> \(\Delta ABH=\Delta ACH\left(cạnhhuyền-cạnhgócvuông\right)\)

=> \(HB=HC\) (2 cạnh tương ứng)

b, Vì \(\Delta ABH=\Delta ACH\left(cạnhhuyền-cạnhgócvuông\right)\left(cmt\right)\)

=> \(\widehat{BAH}=\widehat{CAH}\) (2 góc tương ứng)

CHÚC BẠN HỌC TỐT!

Hình tự vẽ nhé

a, Xét tam giác ABH và tam giác ACH có :

AB=AC

Cạnh AH chung

góc AHB = góc AHC

=> tam giác ABH = tam giác ACH ( cạnh huyền góc nhọn )

Suy ra : HB=HC

b, Ta có : tam giác ABH = tam giác ACH ( câu a )

=> Góc BAH = Góc CAH (2 cạnh tương ứng )
Chúc bạn học tốt

a) Tam giác ABC cân tại A =>Đường cao kẻ từ đỉnh A đồng thời là đường trung tuyến

=.>HB=HC

b) Tam giác ABC cân tại A

=> đường cao đồng thời là đường phân giác

=> góc BAH=góc CAH

còn nhiều thiếu sót mong bạn thông cảm