Xét sự biến thiên của các hàm số
a, y = sinx trên (\(-\dfrac{\pi}{6}\);\(\dfrac{\pi}{3}\))
b, y = cosx trên (\(\dfrac{2\pi}{3}\);\(\dfrac{3\pi}{2}\))
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:
a) y = sinx trên khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right),\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
b) y = cosx trên khoảng \(\left( { - 20\pi ; - 19\pi } \right),\left( { - 9\pi ; - 8\pi } \right)\)
a) y = sinx
- Khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
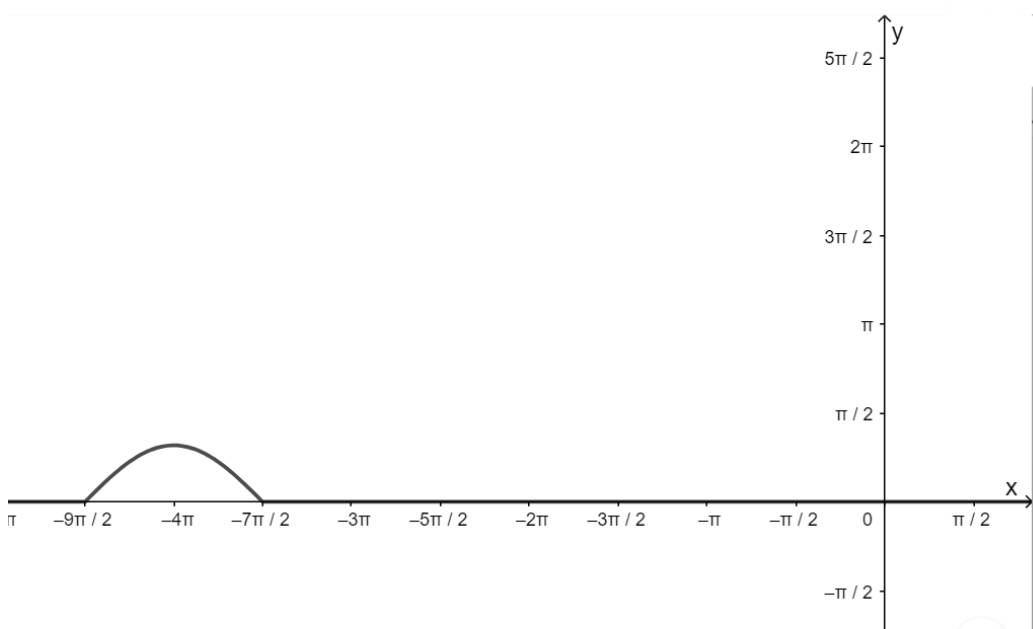
+ Đồng biến trên khoảng \(\left( { - \frac{{9\pi }}{2}; - 4\pi } \right)\)
+ Nghịch biến trên khoảng; \(\left( { - 4\pi ; - \frac{{7\pi }}{2}} \right)\)
- Khoảng \(\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
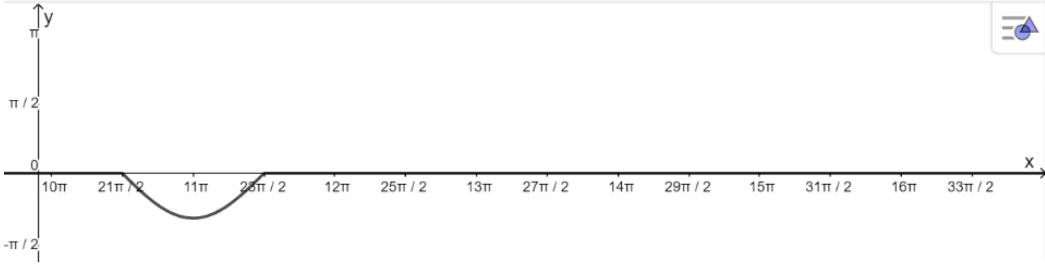
+ Đồng biến trên khoảng: \(\left( {11\pi ;\frac{{23\pi }}{2}} \right)\)
+ Nghịch biến trên khoảng: \(\left( {\frac{{21\pi }}{2};11\pi } \right)\)
Xét tính tăng giảm và lập bảng biến thiên của hàm số y = sin2x trên \(\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]\)
\(y'=-2cos2x=0\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}\\x=\dfrac{\pi}{4}\end{matrix}\right.\)
BBT:
Hàm đồng biến trên \(\left(-\dfrac{\pi}{4};\dfrac{\pi}{4}\right)\) và nghịch biến trên các khoảng \(\left(-\dfrac{\pi}{2};-\dfrac{\pi}{4}\right);\left(\dfrac{\pi}{4};\dfrac{\pi}{2}\right)\)
Xét sự biến thiên của hàm số y = 1 - sinx trên một chu kì tuần hoàn của nó. Trong các kết luận sau, kết luận nào sai?
A. Hàm số đã cho nghịch biến trên khoảng ( - π 2 ; 0)
B. Hàm số đã cho nghịch biến trên khoảng (0; π 2 )
C. Hàm số đã cho đồng biến trên khoảng ( π 2 ; π)
D. Hàm số đã cho nghịch biến trên khoảng ( π 2 ; 3 π 2 )
Đáp án D
Hàm số đã cho tuần hoàn với chu kỳ 2 π và kết hợp với các phương án đề bài thì ta sẽ xét sự biến thiên của hàm số trên (-π/2; 3π/2)
Ta có hàm số y = sin x
* Đồng biến trên khoảng (-π/2; π/2)
* Nghịch biến trên khoảng (π/2; 3π/2)
Từ đây suy ra hàm số y = 1 - sinx
* Nghịch biến trên khoảng (-π/2; π/2)
* Đồng biến trên khoảng (π/2; 3π/2)
Xét sự biến thiên của hàm số y = sinx - cosx. Trong các kết luận sau, kết luận nào đúng?
A. Hàm số đã cho đồng biến trên khoảng ( - π 4 ; 3 π 4 )
B. Hàm số đã cho đồng biến trên khoảng ( 3 π 4 ; 7 π 4 )
C. Hàm số đã cho có tập giá trị là [-1; 1]
D. Hàm số đã cho luôn nghịch biến trên khoảng ( - π 4 ; 7 π 4 )
Đáp án A
Ta có y = sin x - cos x = 2 sin x - π 4
Từ đây ta có thể loại đáp án C, do tập giá trị của hàm số là - 2 ; 2
Hàm số đã cho tuần hoàn với chu kỳ 2π do vậy ta xét sự biến thiên của hàm số trên đoạn (-π/4; 7π/4)
Ta có:
* Hàm số đồng biến trên khoảng (-π/4; 3π/4)
* Hàm số nghịch biến trên khoảng (3π/4; 7π/4)
Xét tính đơn điệu của hàm số y= sinx trên \(\left(-\dfrac{\pi}{2};\dfrac{3\pi}{2}\right)\)
Xét sự biến thiên của hàm số y = sinx - cosx. Tìm kết luận nào đúng?
A. Hàm số đã cho đồng biến trên khoảng ( - π 4 ; 3 π 4 )
B. Hàm số đã cho đồng biến trên khoảng ( 3 π 4 ; 7 π 4 )
C. Hàm số đã cho có tập giá trị là [-1; 1]
D. Hàm số đã cho luôn nghịch biến trên khoảng ( - π 4 ; 7 π 4 )
c1. điều kiện của tham số thực m để phương trình sinx +(m+1)cosx=\(\sqrt{2}\) vô nghiệm là
c2. Hàm số y=sinx đồng biến trên khoảng nào sau đây?
A. \(\left(\dfrac{5\pi}{4},\dfrac{7\pi}{4}\right)\) B.\(\left(\dfrac{9\pi}{4},\dfrac{11\pi}{4}\right)\) C. \(\left(\dfrac{7\pi}{4},3\pi\right)\) D. \(\left(\dfrac{7\pi}{4},\dfrac{9\pi}{4}\right)\)
Giải thích rõ chi tiết cách lm giúp tui với nha, tự học nên mù mờ quá
C1: \(a.sinx+b.cosx=c\)
Pt vô nghiệm \(\Leftrightarrow a^2+b^2< c^2\)
Bạn áp dụng công thức trên sẽ tìm ra m
C2: (Bạn vẽ đường tròn lượng giác sẽ tìm được)
Hàm số \(y=sinx\) đồng biến trên khoảng \(\left(-\dfrac{\pi}{2}+k2\pi;\dfrac{\pi}{2}+k2\pi\right)\) ( góc phần tư thứ IV và I)
Hàm nghịch biến trên khoảng \(\left(\dfrac{\pi}{2}+k2\pi;\dfrac{3\pi}{2}+k2\pi\right)\)( góc phần tư thứ II và III)
Ý A, khoảng nằm trong góc phần tư thứ III và thứ IV => Hàm nghịch biến sau đó đồng biến
Ý B, khoảng nằm trong góc phần tư thứ I và thứ II => hàm đồng biến sau đó nghịch biến
Ý C, khoảng nằm trong góc phần tư thứ IV; I ; II => hàm đồng biền sau đó nghịch biến
Ý D, khoảng nằm trong phần tư thứ IV ; I=> hàm đồng biến
Đ/A: Ý D
(Toi nghĩ thế)
Xét sự đồng biến, nghịch biến của các hàm số :
a) \(y=x-\sin x,x\in\left[0;2\pi\right]\)
b) \(y=x+2\cos x,x\in\left[\dfrac{\pi}{6};\dfrac{5\pi}{6}\right]\)
c) \(y=\sin\dfrac{1}{x},x>0\)
xét sự biến thiên của hàm số sau trên tập xác định của nó và lập bảng biến thiên:
a, \(y=-x^2-2x+3\)
b, \(y=\dfrac{x+1}{x-2}\)
a: TXĐ: D=R
Khi \(x\in D\Rightarrow-x\in D\)
\(f\left(-x\right)=-\left(-x\right)^2-2\cdot\left(-x\right)+3\)
\(=-x^2+2x+3\)
\(\Leftrightarrow f\left(-x\right)\ne f\left(x\right)\ne-f\left(x\right)\)
Vậy: Hàm số không chẵn không lẻ
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = x − sinx, x ∈ [0; 2π].
c) y = sin(1/x), (x > 0)
a) y = x – sinx, x ∈ [0; 2π].
y′ = 1 – cosx ≥ 0 với mọi x ∈ [0; 2π]
Dấu “=” xảy ra chỉ tại x = 0 và x = 2π.
Vậy hàm số đồng biến trên đoạn [0; 2π].
c) Xét hàm số y = sin(1/x) với x > 0.
![]()
Giải bất phương trình sau trên khoảng (0; + ∞ ):
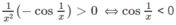
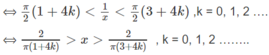
Do đó, hàm số đồng biến trên các khoảng
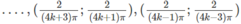
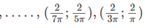
Và nghịch biến trên các khoảng
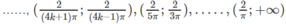
với k = 0, 1, 2 …