Cho tứ diện OABC có OA, OB, OC đôi một vuông góc, OA= 1, OB=2, OC=3
1, tính khoảng cách từ O tới mp ABC
2, gọi I là trung điểm AC, tính khoảng cách từ O đến BI
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc, OA= 1, OB=2, OC=3
1, tính khoảng cách từ O tới mp ABC
2, gọi I là trung điểm AC, tính khoảng cách từ O đến BI
Cho hình chóp tứ giác đều S.ABCD có dáy ABCD là hình vuông cạnh a, các mặt bên của hình chóp tạo vớ mặt phẳng đáy góc 60 độ
1, tính khoảng cách từ A đến mp SAC
2, tính khoảng cách giữa hai đường thẳng AB và SCSC
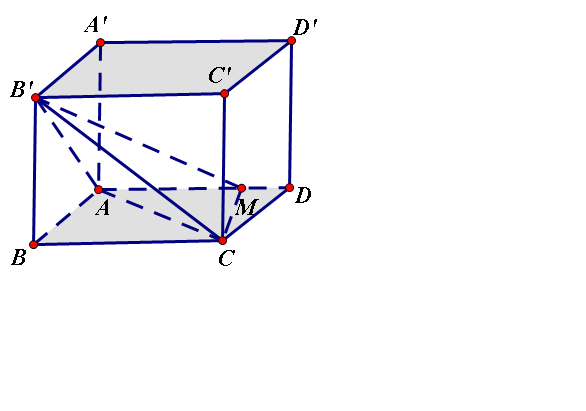
Hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, BC=2a, AA'=a. Lấy điểm M trên cạnh AD sao cho AM=3MD
1, tính khoảng cách từ B đến mp ACB'
2, tính khoảng cách từ M đến mp AB'C
ta có :
\(V_{M.AB'C}=V_{B'.MAC}=\frac{B'B.S_{ABC}}{3}\)
Mà BB'=A'A=a
\(S_{AMC}=\frac{CD.AM}{2}=\frac{a.2a}{2.3}=\frac{a^2}{3}\)
=> \(V_{M.AB'C}=\frac{a^3}{9}\) (1)
=> dM,(AB'C)=\(\frac{3.V_{M.AB'C}}{S_{AB'C}}\) (2)
tam giác AB'C cps \(AB=B'C=2\sqrt{3}\)
và \(AB=a\sqrt{2}\)
=>\(S_{AB'C}=\frac{a^2\sqrt{5}}{2}\) (3)
Từ (1), (2)&(3)
=> dM;(AB'C)=\(\frac{2a}{3\sqrt{a}}\)
Pytago tính đuợc 3 cạnh
, \(MC=\frac{a\sqrt{5}}{2}\)
Dùng công thức Heron =>\(S_{AMC}=\frac{3a^2}{4}\)
\(V_{M.AB'C}=V_{B.AB'C}=\frac{a^3}{4}\)
Mặt khác dùng công thức Heron cũng tính được \(S_{AB'C}=\frac{3a^2}{2}\)
=> \(d_{\left(M;\left(AB'C\right)\right)}=\frac{3V_{M.AB'C}}{S_{AB'C}}=\frac{a}{2}\)
Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân tại C, AB=2a, AA'=a và BC' tạo với mp (ABB'A') 1 góc 60 độ
Gọi N là trung điểm AA', M là trung điểm BB'
Tính d(M,(BC'N))
trước hết phải xác định được góc thì mới tính tiếp nhé.kẻ C'H vuông góc A'B' thì ta có C'H vuông góc A'B' và C'H vuông góc BB' thì C'H vuông góc với cả mp AA'B'B và góc là BC'H=60.giờ tính khoảng cách thông qua thể tích chóp MBNC'.tính diện tích MNB và d(C;MNB) là dễ nhất.ra được thể tích thì tính tiếp diện tích BNC'.rồi lắp vào công thức thể tích là ok thôi
Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a. Hình chiếu của A' lên mặt phẳng (ABC) trùng với trọng tâm G của tam giác ABC. AA'=a, Gọi M, N là trung điểm BC, A'B. Tính khoảng cách từ điểm C đến mặt phẳng (AMN)
Cho hình lăng trụ đứng abca'b'c' có đáy là tam giác abc vuông tại a. Gọi I là trung điểm BC , cho BC =a√6 , góc giữa 2 mp ( a'bc);(abc) bằng 60°.
Tính khoảng cách giữa 2 đường thẳng ab, a'i theo a.
cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại A.AB=3a, BC=5a. hình chiếu vu6ong góc của B' lên (ABC) là tâm đường tròn nội tiếp tam giác ABC . góc giữa (ABB'A') và (ABC) bẳng 60 độ. tính V lăng trụ và khoảng cách từ B' đến (ACC'A')
Tam giác ABC vuông tại A, ta tính được AC:
\(AC^2=BC^2-AB^2=25a^2-9a^2=16a^2\Rightarrow AC-4a\)
Trong mặt phẳng (SAC), qua S kẻ SH vuông góc với AC, H thuộc ACTa có:\(SH=SA.sin30^0=2a\sqrt{3}.\frac{1}{2}=a\sqrt{3}\)\(AH=SA.cos30^0=2a\sqrt{3}.\frac{\sqrt{3}}{2}=3a\)Thể tích khối chóp S.ABC: \(V_{S.ABC}=\frac{1}{2}.SH.S_{\Delta ABC}=\frac{1}{3}.a\sqrt{3}.\frac{1}{2}.3a.4a=2\sqrt{3}a\)Trong mặt phẳng đáy (ABC), qua H kẻ HK vuông góc với BC và cắt BC tại KTam giác HKC đồng dạng với tam giác BAC, ta được:\(\frac{HK}{AB}=\frac{HC}{BC}=\frac{a}{5a}=\frac{1}{5}\rightarrow HK=\frac{1}{5}AB=\frac{1}{5}.3a=\frac{3}{5}a\)Nối SK. Trong mặt phẳng (SHK), từ H kẻ HI vuông góc với SKTa chứng minh được HI vuông góc với mặt phẳng (SBC):Cho hình chóp đều S.ABC đáy ABC có cạnh bằng a mặt bên tạo voiứ mặt đáy một góc bằng phi (0<phi<90) tính khoảng cách từ A đến (SBC)
giúp em với ạ : cho lăng trụ ABC.A'B'C' có đấy là tam giác cân tại A, AB=AC=2a, CAB=120 độ. góc giũa (A'BC)và (ABC) là 45 độ. tính khoảng cách từ B' đến (A'BC)
cho hình chóp SABCD là hình thoi có cạnh bằng a\(\sqrt{3}\) ,góc BAD bằng \(120^0\) và cạnh bên SA vuông góc với mặt phẳng đáy.Biết rằng số đo của góc giữa hai mặt phẳng(SBC) và đáy bằng \(60^0\).khoảng cách giữ hai đường thẳng BD và SC bằng