Bài 4: Ứng dụng hình học của tích phân

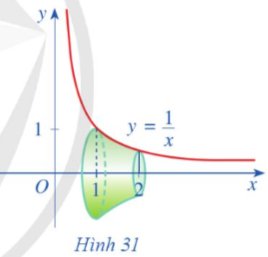
Hình thang cong ABCD ở Hình 28 có diện tích bằng:

A. \(\int\limits^2_1\left(\dfrac{4}{x}-x+3\right)dx\).                        B. \(\int\limits^2_1\left(\dfrac{4}{x}+x-3\right)dx\)

C. \(\int\limits^2_1\left(\dfrac{4}{x}-x-3\right)dx\)                         D. \(\int\limits^4_2\left(\dfrac{4}{x}+x-3\right)dx\)

Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số \(f\left(x\right)=\sqrt{x}\), trục hoành và hai đường thẳng x = 0, x = 2 quay quanh trục Ox là:

A. \(\pi\int\limits^2_0\sqrt{x}dx\).                   B. \(\pi\int\limits^2_0xdx\).                    C. \(\int\limits^2_0\sqrt{x}dx\)                    D. \(\int\limits^2_0xdx\).

Cho đồ thị hàm số y = f(t) như Hình 32.

a) Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(t), trục Ot và hai đường thẳng t = 0, t = 2.

b) Hỏi \(\int\limits^1_0f\left(u\right)du\) biểu thị cho phần diện tích của hình phẳng giới hạn bởi các đường nào trong Hình 32.

Hình 34 minh họa mặt cắt đứng của một con kênh đặt trong hệ trục tọa độ Oxy. Đáy của con kênh là một đường cong cho bởi phương trình \(y=f\left(x\right)=\dfrac{3}{100}\left(-\dfrac{1}{3}x^3+5x^2\right)\).

Hãy tính diện tích hình phẳng tô màu xanh trong Hình 34, biết đơn vị trên mỗi trục tọa độ là mét.

Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox.

Giả sử \(\widehat{POM}=\alpha,OM=l\left(0\le\alpha\le\dfrac{\pi}{3};l>0\right)\).

Gọi 𝒩 là khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox (Hình 35). Tính thể tích của 𝒩 theo α và l.

Sau khi đo kích thước của thùng rượu vang (Hình 36), bạn Quân xác định thùng rượu vang có dạng hình tròn xoay được tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số y = – 0,011x² – 0,071x + 40, trục Ox và hai đường thẳng x = – 35, x = 35 quay quanh trục Ox. Tính thể tích thùng rượu vang đó, biết đơn vị trên mỗi trục tọa độ là centimét.