Trả lời câu hỏi trong hoạt động khởi động trang 52.
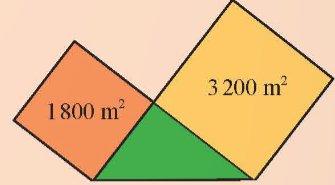
Một khu đất hình tam giác vuông tiếp giáp với hai thửa ruộng hình vuông có diện tích như hình bên. Khu đất hình tam giác vuông có chu vi bằng chu vi thửa ruộng bé không? Kiểm tra bằng cách nào?
Trả lời câu hỏi trong hoạt động khởi động trang 52.
Một khu đất hình tam giác vuông tiếp giáp với hai thửa ruộng hình vuông có diện tích như hình bên. Khu đất hình tam giác vuông có chu vi bằng chu vi thửa ruộng bé không? Kiểm tra bằng cách nào?

Rút gọn các biểu thức sau:
a) \(\frac{2}{3}\sqrt {9{x^3}} + 4x\sqrt {\frac{x}{4}} - {x^2}\sqrt {\frac{1}{x}} \) với x > 0
b) \(\frac{{{a^2} - 5}}{{a + \sqrt {15} }}\) với a \( \ne - \sqrt 5 \)
Thảo luận (1)Hướng dẫn giảia) \(\frac{2}{3}\sqrt {9{x^3}} + 4x\sqrt {\frac{x}{4}} - {x^2}\sqrt {\frac{1}{x}} \)
\(\begin{array}{l} = \frac{2}{3}.3\sqrt {{x^2}.x} + 4x.\frac{1}{2}\sqrt x - \sqrt {{x^4}\frac{1}{x}} \\ = 2x\sqrt x + 2x\sqrt x - \sqrt {{x^3}} \\ = 4x\sqrt x - x\sqrt x \\ = 3x\sqrt x \end{array}\)
b) \(\frac{{{a^2} - 5}}{{a + \sqrt 5 }}\) với a \( \ne - \sqrt 5 \)
\(\frac{{{a^2} - 5}}{{a + \sqrt 5 }} = \frac{{\left( {a + \sqrt 5 } \right)\left( {a - \sqrt 5 } \right)}}{{a + \sqrt 5 }} = a - \sqrt 5 \)
(Trả lời bởi Nguyễn Quốc Đạt)
Rút gọn các biểu thức sau:
a) \(2\sqrt 3 - \sqrt {27} \)
b) \(\sqrt {45} - \sqrt {20} + \sqrt 5 \)
c) \(\sqrt {64a} - \sqrt {18} - a\sqrt {\frac{9}{a}} + \sqrt {50} \) với a > 0
Thảo luận (1)Hướng dẫn giảia) \(2\sqrt 3 - \sqrt {27} \) \( = 2\sqrt 3 - \sqrt {9.3} \) \( = 2\sqrt 3 - 3\sqrt 3 \) \( = - \sqrt 3 \)
b) \(\sqrt {45} - \sqrt {20} + \sqrt 5 \) \( = \sqrt {5.9} - \sqrt {4.5} + \sqrt 5 \) \( = 3\sqrt 5 - 2\sqrt 5 + \sqrt 5 \) \( = 2\sqrt 5 \)
c) \(\sqrt {64a} - \sqrt {18} - a\sqrt {\frac{9}{a}} + \sqrt {50} \) với a > 0
\(\begin{array}{l} = 8\sqrt a - \sqrt {2.9} - 3\sqrt {\frac{{{a^2}}}{a}} + \sqrt {25.2} \\ = 8\sqrt a - 3\sqrt 2 - 3\sqrt a + 5\sqrt 2 \\ = 5\sqrt a + 2\sqrt 2\end{array}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Trục căn thức ở mẫu các biểu thức sau:
a) \(\frac{{2\sqrt 5 }}{{\sqrt 2 }}\)
b) \(\frac{{10}}{{3\sqrt 5 }}\)
c) \( - \frac{3\sqrt a}{\sqrt {12 a}}\) với a > 0
Thảo luận (1)Hướng dẫn giảia) \(\frac{{2\sqrt 5 }}{{\sqrt 2 }} = \frac{{2\sqrt 5 .\sqrt 2 }}{{\sqrt 2 .\sqrt 2 }} = \frac{{2\sqrt {10} }}{2} = \sqrt {10} \)
b) \(\frac{{10}}{{3\sqrt 5 }} = \frac{{10.\sqrt 5 }}{{3\sqrt 5 .\sqrt 5 }} = \frac{{10\sqrt 5 }}{{15}} = \frac{{2\sqrt 5 }}{3}\)
c) \( - \frac{3\sqrt a }{\sqrt {12a}}\) \( = - \frac{3\sqrt a .\sqrt {12a}}{\sqrt {12a} .\sqrt {12a}} \) \(= - \frac{3\sqrt {2^2.3.a^2}}{12a} \) \(= -\frac{6a\sqrt {3}}{12a} \) \(= -\frac{\sqrt {3}}{2} \) với a > 0
(Trả lời bởi Nguyễn Quốc Đạt)
Trục căn thức ở mẫu các biểu thức sau:
a) \(\frac{4}{{\sqrt {13} - 3}}\)
b) \(\frac{{10}}{{5 + 2\sqrt 5 }}\)
c) \(\frac{{\sqrt a - \sqrt b }}{{\sqrt a + \sqrt b }}\) với a > 0; b > 0, \(a \ne b\).
Thảo luận (1)Hướng dẫn giảia) \(\frac{4}{{\sqrt {13} - 3}}\)\( = \frac{{4.\left( {\sqrt {13} + 3} \right)}}{{\left( {\sqrt {13} - 3} \right)\left( {\sqrt {13} + 3} \right)}}\)\( = \frac{{4.\left( {\sqrt {13} + 3} \right)}}{{{{\left( {\sqrt {13} } \right)}^2} - {3^2}}}\)\( = \frac{{4.\left( {\sqrt {13} + 3} \right)}}{{13 - 9}}\)\( = {\sqrt {13} + 3}\)
b) \(\frac{{10}}{{5 + 2\sqrt 5 }}\)\( = \frac{{10.\left( {5 - 2\sqrt 5 } \right)}}{{\left( {5 + 2\sqrt 5 } \right)\left( {5 - 2\sqrt 5 } \right)}}\)\( = \frac{{10.\left( {5 - 2\sqrt 5 } \right)}}{{{5^2} - {{\left( {2\sqrt 5 } \right)}^2}}}\)\( = \frac{{10.\left( {5 - 2\sqrt 5 } \right)}}{5}\)\( = 2\left( {5 - 2\sqrt 5 } \right)\)
c) \(\frac{{\sqrt a - \sqrt b }}{{\sqrt a + \sqrt b }}\)\( = \frac{{\left( {\sqrt a - \sqrt b } \right)\left( {\sqrt a - \sqrt b } \right)}}{{\left( {\sqrt a + \sqrt b } \right)\left( {\sqrt a - \sqrt b } \right)}}\)\( = \frac{{{{\left( {\sqrt a - \sqrt b } \right)}^2}}}{{{{\left( {\sqrt a } \right)}^2} - {{\left( {\sqrt b } \right)}^2}}}\)\( = \frac{{{{\left( {\sqrt a - \sqrt b } \right)}^2}}}{{a - b}}\) với a > 0; b > 0, \(a \ne b\).
(Trả lời bởi Nguyễn Quốc Đạt)
Tính
a) \(\left( {\sqrt {\frac{4}{3}} + \sqrt 3 } \right)\sqrt 6 \)
b) \(\sqrt {18} :\sqrt 6 + \sqrt 8 .\sqrt {\frac{{27}}{2}} \)
c) \({\left( {1 - 2\sqrt 5 } \right)^2}\)
Thảo luận (1)Hướng dẫn giảia) \(\left( {\sqrt {\frac{4}{3}} + \sqrt 3 } \right)\sqrt 6 = \sqrt {\frac{4}{3}} .\sqrt 6 + \sqrt 3 .\sqrt 6 \) \(= \sqrt {\frac{{24}}{3}} + \sqrt {18} \)\(=\sqrt 8 + \sqrt {18} \)\(= \sqrt {2.4} + \sqrt {2.9} \)\(= 2\sqrt 2 + 3\sqrt 2 \)\(= 5\sqrt 2 \)
b) \(\sqrt {18} :\sqrt 6 + \sqrt 8 .\sqrt {\frac{{27}}{2}} \)\( = \sqrt {\frac{{18}}{6}} + \sqrt {8.\frac{{27}}{2}} \)\( = \sqrt 3 + \sqrt {108} \)\( = \sqrt 3 + \sqrt {36.3} \)\( = \sqrt 3 + 6\sqrt 3 \)\( = 7\sqrt 3 \)
c) \({\left( {1 - 2\sqrt 5 } \right)^2} = 1 - 4\sqrt 5 + 20 = 21 - 4\sqrt 5 \)
(Trả lời bởi Nguyễn Quốc Đạt)
Tam giác ABC được vẽ trên ô vuông như Hình 4. Tính diện tích và chu vi của tam giác ABC.
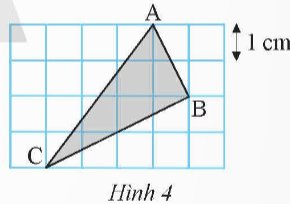
Thảo luận (1)Hướng dẫn giảiTa có:
AB = \(\sqrt{1+2^2} = \sqrt 5\)cm;
BC = \(\sqrt{2^2+4^2} = 2\sqrt 5\)cm;
AC = \(\sqrt{3^2+4^2} = 5\)cm
Chu vi tam giác ABC là: \(\sqrt 5 + 2\sqrt 5 + 5 = 5 + 3 \sqrt5 \)cm
Diện tích tam giác ABC là: \(\frac{1}{2}AB.BC\)= \(\frac{1}{2}.\sqrt 5.2\sqrt 5 = 5\)cm2
(Trả lời bởi Nguyễn Quốc Đạt)
Một vườn hoa gồm ba thửa hình vuông X, Y, Z lần lượt có diện tích như Hình 5. Tính chu vi của vườn hoa đó.
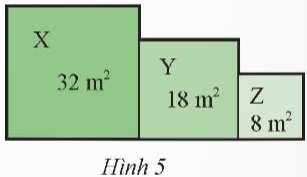
Thảo luận (1)Hướng dẫn giải
Độ dài cạnh hình vuông X là: \(x = \sqrt {32} = 4\sqrt 2 \)m
Độ dài cạnh hình vuông Y là: \(y = \sqrt {18} = 3\sqrt 2 \)m
Ta có cạnh hình vuông Z là: \(z = \sqrt 8 = 2\sqrt 2 \)m
Quan sát hình vẽ ta thấy: AK = BC + DE + FG hay x = BC + DE + FG
Chu vi của vườn hoa là:
\(AB + BC + CD + DE + EF + FG + GH + HI + IK + KA \)
\(= (AB + IK + AK) + (BC + DE + FG) + (CD + HI) + (EF + GH)\)
\(= 3x + x + 2y + 2z\)
\( = 4x + 2y + 2z\)
\( = 4.4\sqrt 2 + 2.3\sqrt 2 + 2.2\sqrt 2 = 26\sqrt 2 (m)\)
Vậy chu vi của vườn hoa đó là: \(26\sqrt 2 \)m.
(Trả lời bởi Nguyễn Quốc Đạt)
Chứng minh rằng:
a) \(\frac{{a\sqrt b - b\sqrt a }}{{\sqrt {ab} }}:\frac{1}{{\sqrt a + \sqrt b }} = a - b\) với a > 0; b > 0
b) \(\left( {1 + \frac{{a + \sqrt a }}{{\sqrt a + 1}}} \right)\left( {1 - \frac{{a - \sqrt a }}{{\sqrt a - 1}}} \right) = 1 - a\) với a \( \ge \) 0 và a \( \ne \)1
Thảo luận (1)Hướng dẫn giảia) \(\frac{{a\sqrt b - b\sqrt a }}{{\sqrt {ab} }}:\frac{1}{{\sqrt a + \sqrt b }} = a - b\) với a > 0; b > 0
Xét vế trái, ta có:
\(\begin{array}{l}VT = \frac{{a\sqrt b - b\sqrt a }}{{\sqrt {ab} }}:\frac{1}{{\sqrt a + \sqrt b }}\\ = \frac{{\sqrt {ab} \left( {\sqrt a - \sqrt b } \right)}}{{\sqrt {ab} }}.\left( {\sqrt a + \sqrt b } \right)\\ = \left( {\sqrt a - \sqrt b } \right)\left( {\sqrt a + \sqrt b } \right)\\ = a - b = VP\end{array}\)
Vậy \(\frac{{a\sqrt b - b\sqrt a }}{{\sqrt {ab} }}:\frac{1}{{\sqrt a + \sqrt b }} = a - b\)
b) \(\left( {1 + \frac{{a + \sqrt a }}{{\sqrt a + 1}}} \right)\left( {1 - \frac{{a - \sqrt a }}{{\sqrt a - 1}}} \right) = 1 - a\) với a \( \ge \) 0 và a \( \ne \)1
Xét vế trái ta có:
\(\left( {1 + \frac{{a + \sqrt a }}{{\sqrt a + 1}}} \right)\left( {1 - \frac{{a - \sqrt a }}{{\sqrt a - 1}}} \right) = \left( {1 + \frac{{\sqrt a \left( {\sqrt a + 1} \right)}}{{\sqrt a + 1}}} \right)\left( {1 - \frac{{\sqrt a \left( {\sqrt a - 1} \right)}}{{\sqrt a - 1}}} \right)\)
\( = \left( {1 + \sqrt a } \right)\left( {1 - \sqrt a } \right) = 1 - {\left( {\sqrt a } \right)^2} = 1 - a\) = VP.
Vậy \(\left( {1 + \frac{{a + \sqrt a }}{{\sqrt a + 1}}} \right)\left( {1 - \frac{{a - \sqrt a }}{{\sqrt a - 1}}} \right) = 1 - a\)
(Trả lời bởi Nguyễn Quốc Đạt)
Khử mẫu của biểu thức lấy căn:
a) \(\sqrt {\frac{4}{7}} \)
b) \(\sqrt {\frac{5}{{24}}} \)
c) \(\sqrt {\frac{2}{{3{a^3}}}} \) với a > 0
d) \(2ab\sqrt {\frac{{{a^2}}}{{2b}}} \) với a < 0, b > 0
Thảo luận (1)Hướng dẫn giảia) \(\sqrt {\frac{4}{7}} = \sqrt {\frac{{4.7}}{{7.7}}} = \frac{{\sqrt {28} }}{7} = \frac{{\sqrt {2^2.7} }}{7} = \frac{{2\sqrt {7} }}{7}\)
b) \(\sqrt {\frac{5}{{24}}} = \sqrt {\frac{{5.24}}{{24.24}}} = \frac{{\sqrt {120} }}{{24}} = \frac{{2\sqrt {30} }}{{24}} = \frac{{\sqrt {30} }}{{12}}\)
c) \(\sqrt {\frac{2}{{3{a^3}}}} = \sqrt {\frac{2}{a^2.3a}} = \sqrt {\frac{1}{a^2}.\frac{2}{3a}} = \left|{\frac{1}{a}}\right| .\sqrt {\frac{2}{3a}}\)
Với a > 0, ta có:
\(\sqrt {\frac{2}{{3{a^3}}}} = {\frac{1}{a}}.\sqrt {\frac{2}{3a}} = {\frac{1}{a}}.\sqrt {\frac{2.3a}{3a.3a}}= \frac{1}{a}.\sqrt {\frac{6a}{9a^2}}\\= {\frac{1}{a}}. \frac{\sqrt{6a}}{3a} = \frac{\sqrt{6a}}{3a^2}\)d) \(2ab\sqrt {\frac{{{a^2}}}{{2b}}} = 2ab\sqrt {\frac{{{a^2}.2b}}{{2b.2b}}} = 2ab\frac{{\sqrt {2b} \left| a \right|}}{{2\left| b \right|}} = - {a^2}\sqrt {2b} \) với a < 0, b > 0
(Trả lời bởi Nguyễn Quốc Đạt)