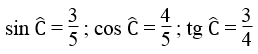Cho tam giác ABC vuông tại A, \(\widehat{B}=30^0;BC=8cm\). Hãy tính cạnh AB (làm tròn đến chữ số thập phân thứ ba), biết rằng \(\cos30^0\approx0,866\)
Bài 2: Tỉ số lượng giác của góc nhọn
Bài 23 (Sách bài tập trang 106)
Thảo luận (1)
Bài 24 (Sách bài tập trang 106)
Cho tam giác ABC vuông tại A, AB = 6 cm, \(\widehat{B}=\alpha\) (h.9).

Biết \(tg\alpha=\dfrac{5}{12}\). Hãy tính :
a) Cạnh AC
b) Cạnh BC
Thảo luận (1)Hướng dẫn giải
Bài 25 (Sách bài tập trang 107)
Tìm giá trị x (làm tròn đến chữ số thập phân thứ ba) trong mỗi tam giác vuông với kích thước được chỉ ra trên hình 10, biết rằng :

Thảo luận (1)Hướng dẫn giảia: \(x=63\cdot\cos47^0\simeq42,966\left(cm\right)\)
b: \(16=x\cdot\cos38^0\)
nên \(x\simeq20,304\left(cm\right)\)
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Bài 26 (Sách bài tập trang 107)
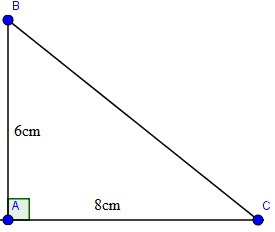
Cho tam giác ABC vuông tại A, trong đó AB = 6cm, AC = 8cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc C ?
Thảo luận (1)Hướng dẫn giải
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2=AB2+AC2=62+82=100BC2=AB2+AC2=62+82=100
Suy ra: BC = 10 (cm)
Ta có:
sinˆB=ACBC=810=0,8sinB^=ACBC=810=0,8
cosˆB=ABBC=610=0,6cosB^=ABBC=610=0,6
tgˆB=ACAB=86=43tgB^=ACAB=86=43
cotgˆC=tgˆB=43
(Trả lời bởi ✿ Hương ➻❥)
Bài 27 (Sách bài tập trang 107)
Cho tam giác ABC vuông tại A. Kẻ đường cao AH. Tính sin B, sin C trong mỗi trường hợp sau (làm tròn đến chữ số thập phân thứ tư ), biết rằng :
a) AB = 13; BH = 5
b) BH = 3 ; CH = 4
Thảo luận (1)Hướng dẫn giảia)
xét tam giác ABH vuông tại H có:
\(AH^2=AB^2-BH^2\Rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{13^2-5^2}=12\)
theo tỉ lệ thức trong tam giác vuông ABC có:
\(AH^2=BH.CH\Rightarrow HC=\frac{AH^2}{BH}=\frac{12^2}{5}=\frac{144}{5}=28,8\)
xét tam giác vuông AHC có:
\(AC^2=AH^2+HC^2\Rightarrow AC=\sqrt{AH^2+HC^2}=\sqrt{12^2+28,8^2}=\frac{156}{5}=31,2\)
vậy : \(\sin B=\frac{AH}{AB}=\frac{12}{13}\)
\(\sin C=\frac{AH}{AC}=\frac{12}{31,2}=\frac{5}{13}\)
b)
theo tỉ số lượng giác trong tam giác ABC có:
\(AH^2=BH.CH\Rightarrow AH=\sqrt{BH.CH}=\sqrt{3.4}=2\sqrt{3}\)
xét tam giác vuông ABH có:
\(AB^2=AH^2+BH^2\Rightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{\left(2\sqrt{3}\right)^2+3^2}=\sqrt{21}\)
theo hệ thức lượng trong tam giác vuông ABC có:
\(AC^2=BC.HC\Rightarrow AC=\sqrt{BC.HC}=\sqrt{7.4}=2\sqrt{7}\)
Vậy : \(\sin B=\frac{AH}{AB}=\frac{2\sqrt{3}}{\sqrt{21}}=\frac{2\sqrt{7}}{7}\)
\(\sin C=\frac{AH}{AC}=\frac{2\sqrt{3}}{2\sqrt{7}}=\frac{\sqrt{21}}{7}\)
(Trả lời bởi Hiệu diệu phương)
Bài 28 (Sách bài tập trang 107)
Hãy biến đổi các tỉ số lượng giác sau đây thành tỉ số lượng giác của các góc nhỏ hơn \(45^0\)?
\(\sin75^0;\cos53^0;\sin47^020';tg62^0;cotg82^045'\)
Thảo luận (1)Hướng dẫn giảisin750 = cos150
(Trả lời bởi Lưu Hạ Vy)
cos530 = sỉn370
sin 47020' = cos 42040'
tan 620 = cot 280
cotg 82045' = tg 7015'
Bài 29 (Sách bài tập trang 107)
Xét quan hệ giữa hai góc trong mỗi biểu thức rồi tính :
a) \(\dfrac{\sin32^0}{\cos58^0}\)
b) \(tg76^0-cotg14^0\)
Thảo luận (1)Hướng dẫn giảia: \(\dfrac{\sin32^0}{\cos58^0}=\dfrac{\sin32^0}{\sin32^0}=1\)
b: \(\tan76^0-\cot14^0=\tan76^0-\tan76^0=0\)
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Bài 30 (Sách bài tập trang 107)
Đường cao MQ của tam giác vuông MNP chia cạnh huyền NP thành hai đoạn NQ = 3, PQ = 6. Hãy so sánh cotg N và cotg P. Tỉ số nào lớn hơn và lớn hơn bao nhiêu lần ?
Thảo luận (2)Hướng dẫn giải(Trả lời bởi Thien Tu Borum)
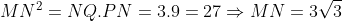
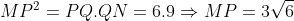
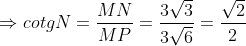
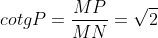
lớn hơn 2 lần
Bài 31 (Sách bài tập trang 108)
Cạnh góc vuông kề với góc \(60^0\) của một tam giác vuông bằng 3. Sử dụng bảng lượng giác của các góc đặc biệt, hãy tìm cạnh huyền và cạnh góc vuông còn lại (làm tròn đến chữ số thập phân thứ tư) ?
Thảo luận (1)Hướng dẫn giảiXét ΔABC vuông tại A có
\(AC=AB\cdot\tan60^0=3\sqrt{3}\simeq5,1962\left(cm\right)\)
=>\(BC=\sqrt{AB^2+AC^2}=6\left(cm\right)\)
(Trả lời bởi Nguyễn Lê Phước Thịnh)
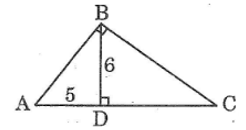
Bài 32 (Sách bài tập trang 108)
Đường cao BD của tam giác nhọn ABC bằng 6; đoạn thẳng AD bằng 5
a) Tính diện tích tam giác ABD
b) Tính AC, dùng các thông tin dưới đây nếu cần :
\(\sin C=\dfrac{3}{5};\cos C=\dfrac{4}{5};tgC=\dfrac{3}{4}\)
Thảo luận (1)Hướng dẫn giải