Trong mặt phẳng (P). Xét một điểm M tùy ý trong không gian.
a) Có bao nhiêu đường thẳng d đi qua điểm M và vuông góc với mặt phẳng (P)?
b) Đường thẳng d cắt mặt phẳng (P) tại bao nhiêu giao điểm?
Trong mặt phẳng (P). Xét một điểm M tùy ý trong không gian.
a) Có bao nhiêu đường thẳng d đi qua điểm M và vuông góc với mặt phẳng (P)?
b) Đường thẳng d cắt mặt phẳng (P) tại bao nhiêu giao điểm?
Cho mặt phẳng (P) và đoạn thẳng AB. Xác định hình chiếu của đoạn thẳng AB trên mặt phẳng (P)
Thảo luận (1)Hướng dẫn giải
Trong Hình 27, mặt sàn gợi nên hình ảnh mặt phẳng (P), đường thẳng a không vuông góc với mặt phẳng (P), đường thẳng a’ là hình chiếu của đường thẳng a trên mặt phẳng (P), đường thẳng d nằm trong mặt phẳng (P). Quan sát Hình 27 và cho biết: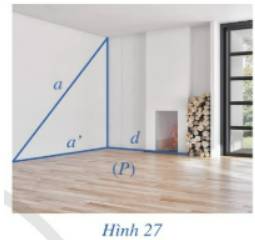
a) Nếu đường thẳng d vuông góc với hình chiếu a’ thì đường thẳng d có vuông góc với a hay không?
b) Ngược lại, nếu dường thẳng d vuông góc với a thì đường thẳng d có vuông góc với hình chiếu a’ hay không
Thảo luận (1)Hướng dẫn giảia: Gọi \(A,B\in a\)
A',B' lần lượt là hình chiếu của A,B trên (P)
\(d\subset\left(P\right)\) nên \(AB\subset\left(P\right)\)
=>d vuông góc A'A
Do đó: nếu d vuông góc a' thì d vuông góc mp(a,a')
=>d vuông góc a
b: Nếu d vuông góc a thì d vuông góc mp(a,a')
=>d vuông góc a'
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Cho hình chóp S.ABCD có \(SA \bot (ABCD)\) và đáy ABCD là hình chữ nhật. Chứng minh rằng các tam giác SBC và SCD là các tam giác vuông
Thảo luận (1)Hướng dẫn giảiVì ABCD là hình chữ nhật nên \(BC \bot AB\).
Vì \(SA \bot (ABCD) \Rightarrow SA \bot AB,\,SA \bot CD\)
+ Ta có:
\(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\\AB \cap SA = A\\AB,\,SA \subset (SAB)\end{array} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot SB\)
Xét \(\Delta SBC\) có \(BC \bot SB \Rightarrow \)Tam giác SBC vuông tại B.
+ Ta có:
\(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\\AD \cap SA = A\\AD,\,SA \subset (SAD)\end{array} \right. \Rightarrow CD \bot (SAD) \Rightarrow CD \bot SD\)
Xét \(\Delta SCD\) có \(CD \bot SD \Rightarrow \)Tam giác SCD vuông tại D.
(Trả lời bởi Hà Quang Minh)
Quan sát Hình 30 (hai cột của biển báo, mặt đường), cho biết hình đó gợi nên tính chất nào về quan hệ vuông góc giữa đường thẳng và mặt phẳng.
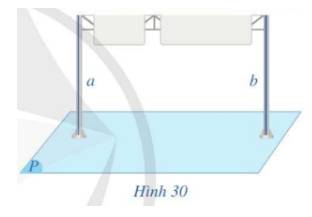
Thảo luận (1)Hướng dẫn giảiGợi lên 2 tính chất:
- Hai đường thẳng vuông góc: Nếu 2 đường thẳng phân biệt cùng vuông góc với 1 mặt phẳng thì chúng song song với nhau
- Hai đường thẳng song song: Một đường thẳng vuông góc với một mặt phẳng thì sẽ vuông góc với tất cả các đường thẳng chứa trong mp đó
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Cho hình chóp S.ABC. Gọi H là hình chiếu của S trên mặt phẳng (ABC).
a) Xác định hình chiếu của các đường thẳng SA, SB, SC trên mặt phẳng (ABC)
b) Giả sử . Chứng minh rằng H là trực tâm của tam giác ABC
Thảo luận (1)Hướng dẫn giảia)
+ H là hình chiếu của S trên mặt phẳng (ABC)
+ A là hình chiếu của A trên mặt phẳng (ABC)
\( \Rightarrow \) HA là hình chiếu của SA trên mặt phẳng (ABC)
+ H là hình chiếu của S trên mặt phẳng (ABC)
+ B là hình chiếu của B trên mặt phẳng (ABC)
\( \Rightarrow \) HB là hình chiếu của SB trên mặt phẳng (ABC)
+ H là hình chiếu của S trên mặt phẳng (ABC)
+ C là hình chiếu của C trên mặt phẳng (ABC)
\( \Rightarrow \) HC là hình chiếu của SC trên mặt phẳng (ABC)
b, Do H là hình chiếu của S trên mặt phẳng (ABC) \( \Rightarrow SH \bot (ABC)\).
Mà \(AB,AC,BC \subset (ABC) \Rightarrow SH \bot AB,SH \bot AC,SH \bot BC\).
Ta có: \(\left\{ \begin{array}{l}SA \bot BC\\SH \bot BC\\SA \cap SH = S\\SA,SH \subset (SAH)\end{array} \right. \Rightarrow BC \bot (SAH) \Rightarrow BC \bot AH\,(1)\)
Tương tự \(\left\{ \begin{array}{l}SC \bot AB\\SH \bot AB\\SC \cap SH = S\\SC,SH \subset (SCH)\end{array} \right. \Rightarrow AB \bot (SCH) \Rightarrow AB \bot CH\,(2)\)
TỪ (1) và (2) \( \Rightarrow \) H là trực tâm của tam giác ABC.
Vì \(\left\{ \begin{array}{l}AB \bot (SCH)\\SC \subset (SCH)\end{array} \right. \Rightarrow AB \bot SC\)
(Trả lời bởi Hà Quang Minh)
Cho tứ diện ABCD có \(AB \bot (BCD)\), các tam giác BCD và ACD là những tam giác nhọn. Gọi H, K lần lượt là trực tâm của các tam giác BCD, ACD (Hình 31). Chứng minh rằng:
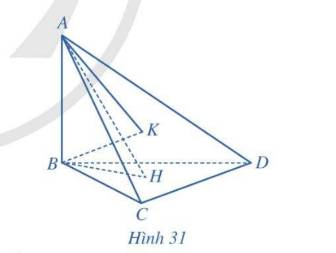
a) \(CD \bot (ABH)\)
b) \(CD \bot (ABK)\)
c) Ba đường thẳng AK, BH, CD cùng đi qua một điểm
Thảo luận (1)Hướng dẫn giảia) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)
Có H là trực tâm của tam giác BCD \( \Rightarrow BH \bot CD\left( 2 \right)\)
Tử (1) và (2) \( \Rightarrow CD \bot \left( {ABH} \right)\)
b) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)
Có K là trực tâm của tam giác BCD \( \Rightarrow AK \bot CD\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow CD \bot \left( {ABK} \right)\)
(Trả lời bởi Quoc Tran Anh Le)
Cho tứ diện ABCD có \(AB \bot (BCD),BC \bot CD\). Gọi M và N lần lượt là hình chiếu vuông góc của B trên AC và AD. Chứng minh rằng:
a) \(CD \bot BM\)
b, \(BM \bot MN\)
Thảo luận (1)Hướng dẫn giảia) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\)
Mà \(CD \bot BC\)\( \Rightarrow CD \bot \left( {ABC} \right)\)
Lại có \(BM \in \left( {ABC} \right)\)\( \Rightarrow CD \bot BM\)
b) Ta có \(\left. \begin{array}{l}BM \bot CD\\BM \bot AC\end{array} \right\} \Rightarrow BM \bot \left( {ACD} \right)\)
Mà \(MN \in \left( {ACD} \right) \Rightarrow BM \bot MN\)
(Trả lời bởi Hà Quang Minh)
Cho hình chóp O.ABC có \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = 90^\circ \). Chứng minh rằng:
a) \(BC \bot OA\)
b) \(CA \bot OB\)
c) \(AB \bot OC\)
Thảo luận (1)Hướng dẫn giảia) Ta có: \(\left. \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OA \bot \left( {OBC} \right)\)
Mà \(BC \in \left( {OBC} \right) \Rightarrow OA \bot BC\)
b) Ta có \(\left. \begin{array}{l}OA \bot OB\\OB \bot OC\end{array} \right\} \Rightarrow OB \bot \left( {OAC} \right)\)
Mà \(CA \in \left( {OAC} \right) \Rightarrow CA \bot OB\)
c) Ta có \(\left. \begin{array}{l}OC \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OC \bot \left( {OAB} \right)\)
Mà \(AB \in \left( {OAB} \right) \Rightarrow AB \bot OC\)
(Trả lời bởi Hà Quang Minh)