a)
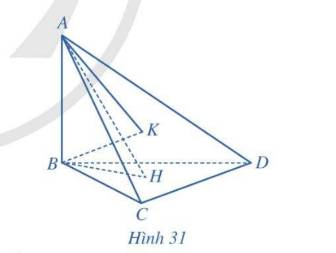
+ H là hình chiếu của S trên mặt phẳng (ABC)
+ A là hình chiếu của A trên mặt phẳng (ABC)
\( \Rightarrow \) HA là hình chiếu của SA trên mặt phẳng (ABC)
+ H là hình chiếu của S trên mặt phẳng (ABC)
+ B là hình chiếu của B trên mặt phẳng (ABC)
\( \Rightarrow \) HB là hình chiếu của SB trên mặt phẳng (ABC)
+ H là hình chiếu của S trên mặt phẳng (ABC)
+ C là hình chiếu của C trên mặt phẳng (ABC)
\( \Rightarrow \) HC là hình chiếu của SC trên mặt phẳng (ABC)
b, Do H là hình chiếu của S trên mặt phẳng (ABC) \( \Rightarrow SH \bot (ABC)\).
Mà \(AB,AC,BC \subset (ABC) \Rightarrow SH \bot AB,SH \bot AC,SH \bot BC\).
Ta có: \(\left\{ \begin{array}{l}SA \bot BC\\SH \bot BC\\SA \cap SH = S\\SA,SH \subset (SAH)\end{array} \right. \Rightarrow BC \bot (SAH) \Rightarrow BC \bot AH\,(1)\)
Tương tự \(\left\{ \begin{array}{l}SC \bot AB\\SH \bot AB\\SC \cap SH = S\\SC,SH \subset (SCH)\end{array} \right. \Rightarrow AB \bot (SCH) \Rightarrow AB \bot CH\,(2)\)
TỪ (1) và (2) \( \Rightarrow \) H là trực tâm của tam giác ABC.
Vì \(\left\{ \begin{array}{l}AB \bot (SCH)\\SC \subset (SCH)\end{array} \right. \Rightarrow AB \bot SC\)