Ta đã biết hạt nhân gồm các proton mang điện dương và các neutron trung hòa về điện. Lực đẩy tĩnh điện giữa các proton là rất lớn vì khoảng cách giữa chúng rất nhỏ. Để duy trì sự tồn tại của hạt nhân, các proton và các neutron (các nucleon) cần một lực hút mạnh hơn lực đẩy tĩnh điện, lực này được gọi là lực hạt nhân. Vậy mức độ liên kết của các nucleon có giống nhau hay không đối với các hạt nhân khác nhau? Độ bền vững của các hạt nhân được đánh giá dựa vào đại lượng vật lí nào?
Bài 15. Năng lượng liên kết hạt nhân
Mở đầu (SGK Chân trời sáng tạo - Trang 100)
Ta đã biết hạt nhân gồm các proton mang điện dương và các neutron trung hòa về điện. Lực đẩy tĩnh điện giữa các proton là rất lớn vì khoảng cách giữa chúng rất nhỏ. Để duy trì sự tồn tại của hạt nhân, các proton và các neutron (các nucleon) cần một lực hút mạnh hơn lực đẩy tĩnh điện, lực này được gọi là lực hạt nhân. Vậy mức độ liên kết của các nucleon có giống nhau hay không đối với các hạt nhân khác nhau? Độ bền vững của các hạt nhân được đánh giá dựa vào đại lượng vật lí nào?
Đọc tiếp
Thảo luận (1)
Câu hỏi 1 (SGK Chân trời sáng tạo - Trang 100)
Tính năng lượng nghỉ của một đồng xu có khối lượng 2 g đang nằm yên trên bàn theo hệ thức về mối liên hệ giữa khối lượng và năng lượng
Thảo luận (1)Hướng dẫn giảiNăng lượng nghỉ của đồng xu là: E = mc2 = 2.10-3.(3.108)2 = 1,8.1014 (J)
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập mục 1 (SGK Chân trời sáng tạo - Trang 101)
Mặt Trời là một nguồn phát năng lượng khổng lồ với công suất rất lớn. Công suất trung bình của Mặt Trời khoảng 4.1026 W. Hãy ước tính khối lượng Mặt Trời mất đi trong mỗi giây để tạo ra được công suất nói trên.
Thảo luận (1)Hướng dẫn giảiNăng lượng của Mặt Trời trong 1 giây là: E = 4.1026 (J)
Khối lượng Mặt Trời mất đi trong mỗi giây là:
\(m = \frac{E}{{{c^2}}} = \frac{{{{4.10}^{26}}}}{{{{({{3.10}^8})}^2}}} = 4,{44.10^9}kg\)
(Trả lời bởi Nguyễn Quốc Đạt)
Câu hỏi 2 (SGK Chân trời sáng tạo - Trang 101)
Hãy ước lượng khối lượng riêng của hạt nhân \(^{12}_6C\). Nhận xét.
Thảo luận (1)Hướng dẫn giảimC = 12 (u) = 1,993.10-26 (kg)
rC = 1,2.10-15.A1/3 = 1,2.10-15.121/3 = 2,75.10-15 (m)
\({V_c} = \frac{4}{3}\pi {r^3} = \frac{4}{3}\pi {(2,{75.10^{ - 15}})^3} = 8,{71.10^{ - 44}}{m^3}\)
\( \to d = \frac{m}{V} = \frac{{1,{{993.10}^{ - 26}}}}{{8,{{71.10}^{ - 44}}}} = 2,{3.10^{17}}kg/{m^3}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Câu hỏi 3 (SGK Chân trời sáng tạo - Trang 102)
Sử dụng hệ thức E = mc2 để xác định năng lượng của các hạt trong Bảng 15.1 theo đơn vị MeV và J.
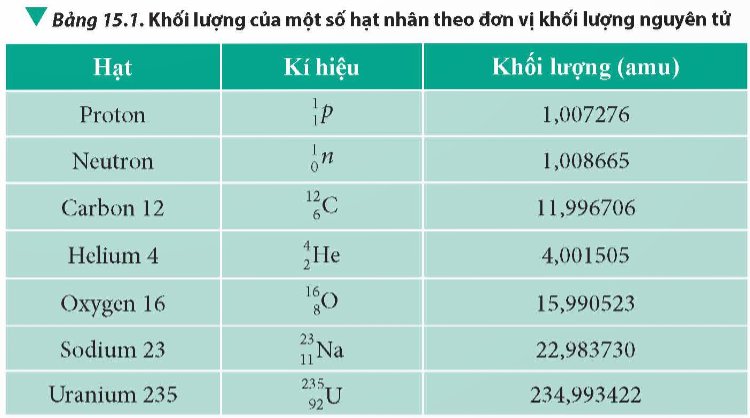
Thảo luận (1)Hướng dẫn giải(Trả lời bởi Nguyễn Quốc Đạt)
Hạt
Kí hiệu
Khối lượng (amu)
Năng lượng (MeV)
Năng lượng (J)
Proton
\({}_1^1H\)
1,007276
938,28
1,51.10-10
Neutron
\({}_0^1n\)
1,008665
939,57
1,51.10-10
Carbon 12
\({}_6^{12}C\)
11,996706
11174,93
1,79.10-9
Helium 4
\({}_2^4He\)
4,001505
3727,4
5,98.10-10
Oxygen 16
\({}_8^{16}O\)
15,990523
14895,17
2,39.10-9
Sodium 23
\({}_{11}^{23}Na\)
22,983730
21409,34
2,68.10-8
Uranium 235
\({}_{92}^{235}U\)
234,993422
218896,37
3,51.10-8
Câu hỏi 4 (SGK Chân trời sáng tạo - Trang 102)
So sánh lực đẩy tĩnh điện và lực hấp dẫn giữa hai proton đặt cách nhau 1 fm. Biết rằng điện tích của proton là 1,6.10-19 C và lực hấp dẫn giữa hai proton ở khoảng cách 1 fm là 1,87.10-34 N
Thảo luận (1)Hướng dẫn giải\({F_d} = k\frac{{{q_1}{q_2}}}{{{r^2}}} = {9.10^9}\frac{{{{(1,{{6.10}^{ - 19}})}^2}}}{{{{({{1.10}^{ - 15}})}^2}}} = 230,4N\)
→ Lực đẩy tĩnh điện lớn hơn rất nhiều so với lực hấp dẫn giữa hai proton cách nhau 1fm.
(Trả lời bởi Nguyễn Quốc Đạt)
Câu hỏi 5 (SGK Chân trời sáng tạo - Trang 103)
Tính độ hụt khối của hai hạt nhân bất kì được cho trong Bảng 15.1.
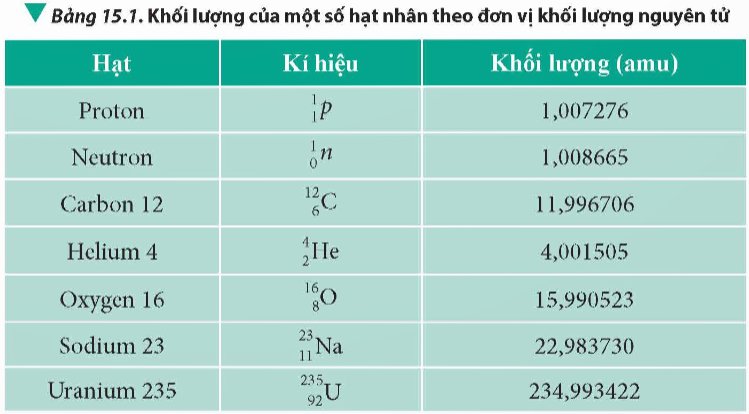
Thảo luận (1)Hướng dẫn giảimHe = (2.1,007276 + 2.1,008665) - 4,001505 = 0,030377 (amu)
∆mO = (8.1,007276 + 8.1,008665) - 15,990523 = 0,137005 (amu)
(Trả lời bởi Nguyễn Quốc Đạt)
Câu hỏi 6 (SGK Chân trời sáng tạo - Trang 103)
Tính năng lượng liên kết của hai hạt nhân bất kì được cho trong Bảng 15.1.

Thảo luận (1)Hướng dẫn giảiElk (He) = 0,030377.931,5 = 28,3 (MeV)
Elk (O) = 0,137005.931,5 = 127,62 (MeV)
(Trả lời bởi Nguyễn Quốc Đạt)
Câu hỏi 7 (SGK Chân trời sáng tạo - Trang 104)
Tính năng lượng liên kết riêng của các hạt nhân \(^{12}_6C,^4_2He,^{16}_8O,^{235}_{92}U\) trong Bảng 15.1 và chỉ ra trong đó hạt nhân nào bền vững nhất và kém bền vững nhất.
Thảo luận (1)Hướng dẫn giải\({E_{lkr}} = \frac{{{E_{lk}}}}{A} = \frac{{\Delta m{c^2}}}{A}\)
\({E_{lkr(C)}} = \frac{{\left( {\left( {6.1,007276 + 6.1,008665} \right) - 11,996706} \right).931,5}}{{12}} = 7,68MeV/nucleon\)
\({E_{lkr(He)}} = \frac{{\left( {\left( {2.1,007276 + 2.1,008665} \right) - 4,001505} \right).931,5}}{4} = 7,07MeV/nucleon\)
\({E_{lkr(O)}} = \frac{{\left( {\left( {8.1,007276 + 8.1,008665} \right) - 15,990523} \right).931,5}}{{16}} = 7,98MeV/nucleon\)
\({E_{lkr(U)}} = \frac{{\left( {\left( {92.1,007276 + 143.1,008665} \right) - 234,993422} \right).931,5}}{{235}} = 7,59MeV/nucleon\)
Hạt nhân bền vững nhất là \({}_8^{16}O\); Hạt nhân kém bền vững nhất là \({}_2^4He\)
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập mục 3 (SGK Chân trời sáng tạo - Trang 104)
Hãy thảo luận và giải thích tại sao hạt nhân \(^1_1H\) không xuất hiện trong Hình 15.2.
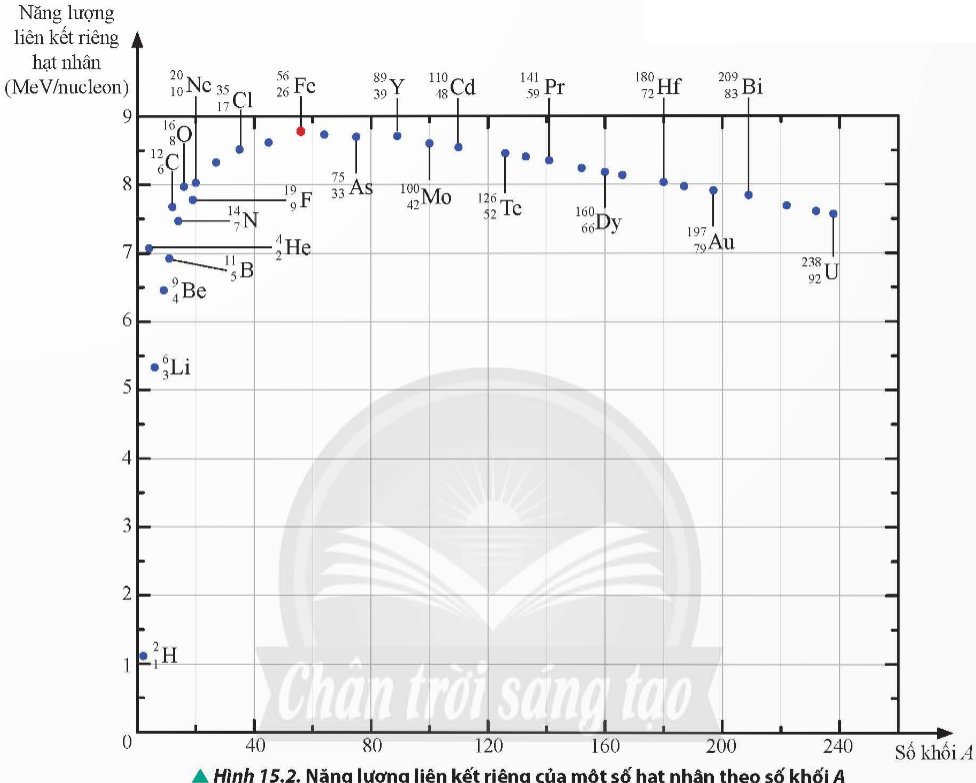
Thảo luận (1)Hướng dẫn giảiVì hạt nhân \({}_1^1H\) chỉ có duy nhất 1 proton nên không có năng lượng liên kết.
(Trả lời bởi Nguyễn Quốc Đạt)