Bằng cách viết lại các hàm số sau dưới dạng hàm số lũy thừa y = xα (x > 0), hãy tính đạo hàm của các hàm số sau với x > 0: \(y=\dfrac{1}{x^4};y=x^{\sqrt{2}};y=\dfrac{1}{\sqrt[3]{x}}\).
Bài 11. Nguyên hàm
Câu hỏi mục 3 (SGK Kết nối tri thức với cuộc sống - Trang 8)
Thảo luận (1)
Hoạt động 5 (SGK Kết nối tri thức với cuộc sống - Trang 8)
a) Với α ≠ −1, tính đạo hàm của hàm số \(y=\dfrac{x^{\alpha+1}}{\alpha+1}\left(x>0\right).\)
b) Cho hàm số y = ln|x| (x ≠ 0). Tính đạo hàm của hàm số này trong hai trường hợp: x > 0 và x < 0.
Thảo luận (1)Hướng dẫn giảia) Vì \(y' = {\left( {\frac{{{x^{\alpha + 1}}}}{{\alpha + 1}}} \right)'} = \frac{{\left( {\alpha + 1} \right){x^\alpha }}}{{\alpha + 1}} = {x^\alpha }\) với mọi \(x > 0\), \(\alpha \ne - 1\).
b) Ta có: \(y' = \left( {\ln \left| x \right|} \right)' = \frac{1}{{\left| x \right|}}\).
Với \(x > 0\) thì \(y' = \frac{1}{x}\).
Với \(x < 0\) thì \(y' = \frac{1}{{ - x}}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 5 (SGK Kết nối tri thức với cuộc sống - Trang 9)
Tìm:
a) \(\int\dfrac{1}{x^4}dx;\) b) \(\int x\sqrt{x}dx\) (x > 0); c) \(\int\left(\dfrac{3}{x}-5\sqrt[3]{x}\right)dx\) (x > 0).
Thảo luận (1)Hướng dẫn giảia) \(\int {\frac{1}{{{x^4}}}dx} = \int {{x^{ - 4}}dx} = \frac{{{x^{ - 4 + 1}}}}{{ - 4 + 1}} + C = \frac{{{x^{ - 3}}}}{{ - 3}} + C = \frac{{ - 1}}{{3{x^3}}} + C\);
b) \(\int {x\sqrt x dx = } \int {{x^{\frac{3}{2}}}dx = } \frac{{{x^{\frac{3}{2} + 1}}}}{{\frac{3}{2} + 1}} + C = \frac{2}{5}{x^2}\sqrt x + C\);
c) \(\int {\left( {\frac{3}{x} - 5\sqrt[3]{x}} \right)dx = \int {\frac{3}{x}dx - \int {5\sqrt[3]{x}} dx = 3\int {\frac{1}{x}dx - 5\int {{x^{\frac{1}{3}}}} dx = 3\ln \left| x \right| - 5.\frac{{{x^{\frac{4}{3}}}}}{{\frac{4}{3}}} + C} } } \)
\( = 3\ln \left| x \right| - \frac{{15x\sqrt[3]{x}}}{4} + C\).
(Trả lời bởi Nguyễn Quốc Đạt)
Hoạt động 6 (SGK Kết nối tri thức với cuộc sống - Trang 9)
a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.
Đọc tiếp
a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.

b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.

Thảo luận (1)Hướng dẫn giải
Luyện tập 6 (SGK Kết nối tri thức với cuộc sống - Trang 9)
Tìm:
a) \(\int\left(3\cos x-4\sin x\right)dx;\) b) \(\int\left(\dfrac{1}{\cos^2x}-\dfrac{1}{\sin^2x}\right)dx.\)
Thảo luận (1)Hướng dẫn giảia) \(\int {\left( {3\cos x - 4\sin x} \right)dx} = 3\int {\cos x} dx - 4\int {\sin x} dx = 3\sin x + 4\cos x + C\);
b) \(\int {\left( {\frac{1}{{{{\cos }^2}x}} - \frac{1}{{{{\sin }^2}x}}} \right)dx} = \int {\frac{1}{{{{\cos }^2}x}}} dx - \int {\frac{1}{{{{\sin }^2}x}}} dx = \tan x + \cot x + C\).
(Trả lời bởi Nguyễn Quốc Đạt)
Hoạt động 7 (SGK Kết nối tri thức với cuộc sống - Trang 10)
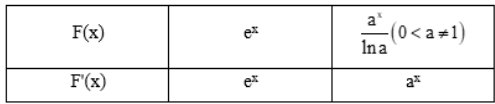
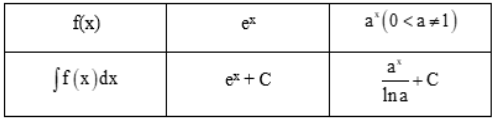
a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.
Đọc tiếp
a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.

b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.

Thảo luận (1)Hướng dẫn giải
Luyện tập 7 (SGK Kết nối tri thức với cuộc sống - Trang 10)
Tìm:
a) \(\int4^xdx;\) b) \(\int\dfrac{1}{e^x}dx;\) c) \(\int\left(2.3^x-\dfrac{1}{3}.7^x\right)dx.\)
Thảo luận (1)Hướng dẫn giảia) \(\int {{4^x}dx} = \frac{{{4^x}}}{{\ln 4}} + C\);
b) \(\int {\frac{1}{{{e^x}}}dx} = \int {{{\left( {\frac{1}{e}} \right)}^x}dx} = \frac{{{{\left( {\frac{1}{e}} \right)}^x}}}{{\ln \frac{1}{e}}} + C = - {e^{ - x}} + C\);
c) \(\int {\left( {{{2.3}^x} - \frac{1}{3}{{.7}^x}} \right)dx} = 2\int {{3^x}} dx - \frac{1}{3}\int {{7^x}} dx = \frac{{{{2.3}^x}}}{{\ln 3}} - \frac{{{7^x}}}{{3\ln 7}} + C\).
(Trả lời bởi Nguyễn Quốc Đạt)
Bài 4.1 (SGK Kết nối tri thức với cuộc sống - Trang 11)
Trong mỗi trường hợp sau, hàm số F(x) có là một nguyên hàm của hàm số f(x) trên khoảng tương ứng không? Vì sao?
a) F(x) = xlnx và f(x) = 1 + lnx trên khoảng (0; +∞);
b) F(x) = esinx và f(x) = ecosx trên ℝ.
Thảo luận (1)Hướng dẫn giảia) Ta có: \(F'\left( x \right) = \left( {x\ln x} \right)' = \ln x + \frac{x}{x} = \ln x + 1\). Do đó, \(F'\left( x \right) = f\left( x \right)\) với mọi x thuộc \(\left( {0; + \infty } \right)\). Do đó, F(x) là một nguyên hàm của hàm số f(x) trên khoảng \(\left( {0; + \infty } \right)\).
b) Ta có: \(F'\left( x \right) = \left( {{e^{\sin x}}} \right)' = \cos x.{e^{\sin x}}\).
Hàm số F(x) không là một nguyên hàm của hàm số f(x) trên \(\mathbb{R}\) vì \(F'\left( {\frac{\pi }{2}} \right) = 0 \ne 1 = f\left( 1 \right)\)
(Trả lời bởi Nguyễn Quốc Đạt)
Bài 4.2 (SGK Kết nối tri thức với cuộc sống - Trang 11)
Tìm nguyên hàm của các hàm số sau:
a) f(x) = 3x2 + 2x – 1; b) f(x) = x3 – x;
c) f(x) = (2x + 1)2; d) \(f\left(x\right)=\left(2x-\dfrac{1}{x}\right)^2\).
Thảo luận (1)Hướng dẫn giảia) \(\int {\left( {3{x^2} + 2x - 1} \right)} dx = 3\int {{x^2}} dx + 2\int x dx - \int 1 dx = {x^3} + {x^2} - x + C\)
b) \(\int {\left( {{x^3} - x} \right)} dx = \int {{x^3}} dx - \int x dx = \frac{{{x^4}}}{4} - \frac{{{x^2}}}{2} + C\)
c) \(\int {{{\left( {2x + 1} \right)}^2}} dx = \int {\left( {4{x^2} + 4x + 1} \right)} dx = 4\int {{x^2}} dx + 4\int x dx + \int 1 dx = \frac{{4{x^3}}}{3} + 2{x^2} + x + C\)
d) \(\int {{{\left( {2x - \frac{1}{x}} \right)}^2}} dx = \int {\left( {4{x^2} - 4 + \frac{1}{{{x^2}}}} \right)} dx = 4\int {{x^2}} dx + \int {{x^{ - 2}}} dx - 4\int 1 dx = \frac{{4{x^3}}}{3} - \frac{1}{x} - 4x + C\)
(Trả lời bởi Nguyễn Quốc Đạt)
Bài 4.3 (SGK Kết nối tri thức với cuộc sống - Trang 11)
Tìm:
a) \(\int\left(3\sqrt{x}+\dfrac{1}{\sqrt[3]{x}}\right)dx;\) b) \(\int\left(7x^2-3\right)dx\) (x > 0);
c) \(\int\dfrac{\left(2x+1\right)^2}{x^2}dx;\) d) \(\int\left(2^x+\dfrac{3}{x^2}\right)dx.\)
Thảo luận (1)Hướng dẫn giảia) \(\int {\left( {3\sqrt x + \frac{1}{{\sqrt[3]{x}}}} \right)} dx = 3\int {{x^{\frac{1}{2}}}} dx + \int {{x^{\frac{{ - 1}}{3}}}} dx = 2x\sqrt x + \frac{3}{2}\sqrt[3]{{{x^2}}} + C\)
b) \(\int {\sqrt x \left( {7{x^2} - 3} \right)} dx = \int {\left( {7{x^{\frac{5}{2}}} - 3{x^{\frac{1}{2}}}} \right)dx = } 7\int {{x^{\frac{5}{2}}}} dx - 3\int {{x^{\frac{1}{2}}}} dx = 2{x^3}\sqrt x - 2x\sqrt x + C\)
c) \(\int {\frac{{{{\left( {2x + 1} \right)}^2}}}{{{x^2}}}} dx = \int {\frac{{4{x^2} + 4x + 1}}{{{x^2}}}} dx = \int 4 dx + 4\int {\frac{1}{x}} dx + \int {{x^{ - 2}}} dx = 4x + 4\ln \left| x \right| - \frac{1}{x} + C\)
d) \(\int {\left( {{2^x} + \frac{3}{{{x^2}}}} \right)} dx = \int {{2^x}} dx + 3\int {{x^{ - 2}}} dx = \frac{{{2^x}}}{{\ln 2}} - \frac{3}{x} + C\)
(Trả lời bởi Nguyễn Quốc Đạt)