Bài 1: Xác suất có điều kiện

Hướng dẫn giải

a) Khi biến cố \(A\) xảy ra, tức là viên bi lấy ra lần thứ nhất là viên bi màu xanh. Bỏ viên bi màu xanh đó vào túi thứ hai, lúc này trong túi thứ 2 ta có 3 viên bi xanh và 3 viên bi đỏ.

Khi đó, xác suất để lấy ra được viên bi đỏ ở túi thứ hai (cũng là xác suất của biến cố \(B\)) là \(P\left( B \right) = \frac{3}{6} = \frac{1}{2}\).

b) Khi biến cố \(A\) không xảy ra, tức là viên bi lấy ra lần thứ nhất là viên bi màu đỏ. Bỏ viên bi màu đỏ đó vào túi thứ hai, lúc này trong túi thứ hai ta có 2 viên bi xanh và 4 viên bi đỏ. Khi đó, xác suất để lấy ra được viên bi đỏ ở túi thứ hai (cũng là xác suất của biến cố \(B\)) là \(P\left( B \right) = \frac{4}{6} = \frac{2}{3}\).

(Trả lời bởi datcoder)

Hướng dẫn giải

Tính \(P\left( {D|A} \right)\), tức là tính xác suất của biến cố

\(D\) với điều kiện \(A\). Khi biến cố \(A\) xảy ra thì kết quả của phép thử sẽ là \(\left( {1;2} \right)\) hoặc \(\left( {1;3} \right)\). Cả hai kết quả này đều có lợi cho biến cố \(D\). Suy ra \(P\left( {D|A} \right) = 1\).

Tính \(P\left( {D|B} \right)\), tức là tính xác suất của biến cố \(D\) với điều kiện \(B\). Khi biến cố \(B\) xảy ra thì kết quả của phép thử là \(\left( {2;1} \right)\) hoặc \(\left( {2;3} \right)\). Trong hai kết quả trên, chỉ có kết quả \(\left( {2;3} \right)\) là có lợi cho biến cố \(D\). Suy ra \(P\left( {D|B} \right) = \frac{1}{2}\).

(Trả lời bởi datcoder)

Hướng dẫn giải

Số thành viên biết chơi cả hai môn cờ tướng và cờ vua là: \(25 + 20 - 35 = 10\)(người)

Gọi \(A\) là biến cố “Thành viên được chọn không biết chơi cờ tướng”, \(B\) là biến cố “Thành viên đó biết chơi cờ vua”. Ta cần tính \(P\left( {A|B} \right)\).

Khi biến cố \(B\) xảy ra, ta thấy có 25 kết quả thuận lợi cho \(B\) (tức là 25 thành viên biết chơi cờ vua). Trong số đó, có 15 kết quả thuận lợi cho biến cố \(A\) (do có 10 thành viên biết chơi cả 2 môn cờ, nên sẽ có \(25 - 10 = 15\) người không biết chơi cờ tướng).

Vậy \(P\left( {A|B} \right) = \frac{{15}}{{25}} = \frac{3}{5}\).

(Trả lời bởi datcoder)

Hướng dẫn giải

Gọi \(A\) là biến cố “Xuất hiện mặt chẵn chấm” và \(B\) là biến cố “Xuất hiện mặt 6 chấm”. Ta phải tìm \(P\left( {B|A} \right)\).

Khi biến cố \(A\) xuất hiện, các kết quả của phép thử sẽ là 2, 4, 6. Chỉ có duy nhất kết quả 6 là có lợi cho biến cố \(B\). Vậy \(P\left( {B|A} \right) = \frac{1}{3}\).

(Trả lời bởi datcoder)

Hướng dẫn giải

a) Ta dễ dàng thấy các kết quả \(\left( {3;5} \right)\); \(\left( {4;4} \right)\); \(\left( {5;3} \right)\) là có lợi cho biến cố \(B\), suy ra \(P\left( B \right) = \frac{3}{{36}} = \frac{1}{{12}}\).

Biến cố \(A \cap B\) là biến cố “Xuất hiện hai mặt cùng số chấm và tổng số chấm của hai mặt xuất hiện là 8”. Dễ dàng thấy \(\left( {4;4} \right)\) là kết quả có lợi duy nhất của biến cố này. Vậy \(P\left( {A \cap B} \right) = \frac{1}{{36}}\). Suy ra \(\frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}} = \frac{{\frac{1}{{36}}}}{{\frac{1}{{12}}}} = \frac{1}{3}\).

Khi biến cố \(B\) xảy ra, ta thấy chỉ có 1 kết quả có lợi cho biến cố \(A\). Như vậy \(P\left( {A|B} \right) = \frac{1}{3}\).

b) Ta dễ dàng thấy các kết quả \(\left( {1;1} \right)\); \(\left( {2;2} \right)\); \(\left( {3;3} \right)\); \(\left( {4;4} \right)\); \(\left( {5;5} \right)\); \(\left( {6;6} \right)\) là các kết quả có lợi cho biến cố \(A\). Suy ra \(P\left( A \right) = \frac{6}{{36}} = \frac{1}{6}\).

Biến cố \(C \cap A\) là biến cố “Xuất hiện hai mặt cùng số chấm và có ít nhất một mặt 6 chấm”. Dễ dàng thấy \(\left( {6;6} \right)\) là kết quả có lợi duy nhất của biến cố này. Vậy \(P\left( {C \cap A} \right) = \frac{1}{{36}}\). Suy ra \(\frac{{P\left( {C \cap A} \right)}}{{P\left( A \right)}} = \frac{{\frac{1}{{36}}}}{{\frac{1}{6}}} = \frac{1}{6}\).

Khi biến cố \(A\) xảy ra, ta thấy chỉ có 1 kết quả có lợi cho biến cố \(C\). Như vậy \(P\left( {C|A} \right) = \frac{1}{6}\).

(Trả lời bởi datcoder)

Hướng dẫn giải

Gọi \(A\) là biến cố “Hai bạn được chọn cùng giới tính” và \(B\) là biến cố “Hai bạn được chọn có ít nhất một bạn nam”. Ta cần phải tính \(P\left( {A|B} \right)\).

Số cách chọn hai bạn bất kì là \(C_9^2 = 45\).

Số cách chọn hai bạn nam là \(C_5^2 = 10\).

Số cách chọn hai bạn nữ là \(C_4^2 = 6\).

Biến cố \(AB\) là biến cố “Hai bạn được chọn có cùng giới tính và có ít nhất một bạn nam”, đồng nghĩa với “Hai bạn được chọn là hai bạn nam”. Suy ra \(P\left( {AB} \right) = \frac{{10}}{{45}} = \frac{2}{9}\)

Xác suất của biến cố \(B\) là \(P\left( B \right) = \frac{{45 - 6}}{{45}} = \frac{{13}}{{15}}\).

Như vậy \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{\frac{2}{9}}}{{\frac{{13}}{{15}}}} = \frac{{10}}{{39}}\).

(Trả lời bởi datcoder)

Hướng dẫn giải

Gọi \(A\) là biến cố “Bệnh nhân bị chấn thương vùng đầu”, \(B\) là biến cố “Bệnh nhân đội mũ bảo hiểm đúng cách”.

Theo đề bài, ta có \(P\left( A \right) = 80\%  = 0,8\); \(P\left( B \right) = 90\%  = 0,9\).

Biến cố \[AB\] là biến cố “Bệnh nhân đội mũ bảo hiểm đúng cách bị chấn thương vùng đầu”. Theo đề bài, ta có \(P\left( {AB} \right) = 18\%  = 0,18\).

Khi biến cố \(B\) xảy ra, tức là bệnh nhân đội mũ bảo hiểm đúng cách, ta cần tính xác suất để bệnh nhân bị chấn thương vùng đầu, tức là tính \(P\left( {A|B} \right)\).

Ta có \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{0,18}}{{0,9}} = 0,2\).

Như vậy, khi đội mũ bảo hiểm đúng cách thì tỉ lệ chấn thương vùng đầu sẽ là 0,2. Suy ra việc đội mũ bảo hiểm đúng cách sẽ làm giảm khả năng chấn thương vùng đầu đi \(\frac{{0,8}}{{0,2}} = 4\) lần.

(Trả lời bởi datcoder)

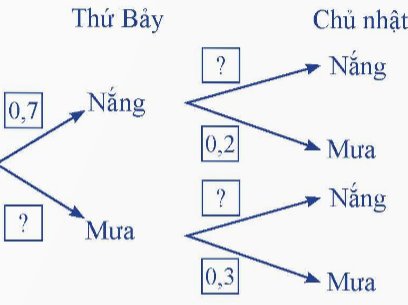
Hướng dẫn giải

Với ngày thứ 7, xác suất trời nắng là \(0,7\) nên xác suất trời mưa là \(1 - 0,7 = 0,3\).

Với ngày Chủ nhật:

- Trong trường hợp ngày thứ 7 trời nắng, xác suất trời mưa trong ngày Chủ nhật là \(0,2\). Suy ra xác suất trời nắng trong ngày Chủ nhật là \(1 - 0,2 = 0,8\).

- Trong trường hợp ngày thứ 7 trời mưa, xác suất trời mưa trong ngày Chủ nhật là \(0,3\). Suy ra xác suất trời nắng trong ngày Chủ nhật là \(1 - 0,3 = 0,7\).

Ta có sơ đồ sau:

(Trả lời bởi datcoder)

Hướng dẫn giải

Gọi \(M\) là biến cố “Viên bi lấy ra ở hộp thứ nhất có màu xanh” và \(N\) là biến cố “Viên bi lấy ra ở hộp thứ hai có màu đỏ”.

Xác suất để lấy ra được 1 viên bi xanh ở hộp thứ nhất là \(\frac{4}{{10}} = 0,4\).

Nếu ta lấy được viên bi xanh ở hộp thứ nhất và bỏ vào hộp thứ hai thì hộp thứ hai có 6 viên bi xanh và 4 viên bi đỏ. Suy ra xác suất để lấy ra được 1 viên bi đỏ là \(\frac{4}{{10}} = 0,4\).

Nếu ta lấy được viên bi đỏ ở hộp thứ nhất và bỏ vào hộp thứ hai thì hộp thứ hai có 5 viên bi xanh và 5 viên bi đỏ. Suy ra xác suất để lấy được 1 viên bi đỏ là \(\frac{5}{{10}} = 0,5\).

Ta có sơ đồ hình cây sau:

Dựa vào sơ đồ hình cây, ta có:

\(P\left( A \right) = P\left( {MN} \right) = 0,16.\)

\(P\left( B \right) = P\left( {M\bar N} \right) + P\left( {\bar MN} \right) = 0,24 + 0,3 = 0,54.\)

(Trả lời bởi datcoder)