Hộp thứ nhất có 4 viên bi xanh và 6 viên bi đỏ. Hộp thứ hai có 5 viên bi xanh và 4 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên 1 viên bi từ hộp thứ hai.
Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:
A: “Viên bi lấy ra từ hộp thứ nhất có màu xanh và viên bi lấy ra từ hộp thứ hai có màu đỏ”;
B: “Hai viên bi lấy ra có cùng màu”.
Gọi \(M\) là biến cố “Viên bi lấy ra ở hộp thứ nhất có màu xanh” và \(N\) là biến cố “Viên bi lấy ra ở hộp thứ hai có màu đỏ”.
Xác suất để lấy ra được 1 viên bi xanh ở hộp thứ nhất là \(\frac{4}{{10}} = 0,4\).
Nếu ta lấy được viên bi xanh ở hộp thứ nhất và bỏ vào hộp thứ hai thì hộp thứ hai có 6 viên bi xanh và 4 viên bi đỏ. Suy ra xác suất để lấy ra được 1 viên bi đỏ là \(\frac{4}{{10}} = 0,4\).
Nếu ta lấy được viên bi đỏ ở hộp thứ nhất và bỏ vào hộp thứ hai thì hộp thứ hai có 5 viên bi xanh và 5 viên bi đỏ. Suy ra xác suất để lấy được 1 viên bi đỏ là \(\frac{5}{{10}} = 0,5\).
Ta có sơ đồ hình cây sau:
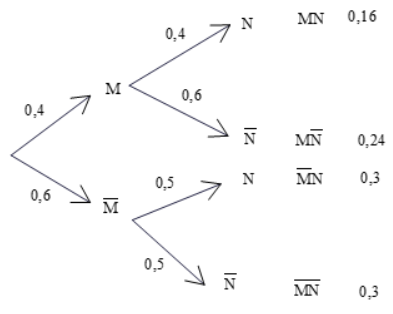
Dựa vào sơ đồ hình cây, ta có:
\(P\left( A \right) = P\left( {MN} \right) = 0,16.\)
\(P\left( B \right) = P\left( {M\bar N} \right) + P\left( {\bar MN} \right) = 0,24 + 0,3 = 0,54.\)


