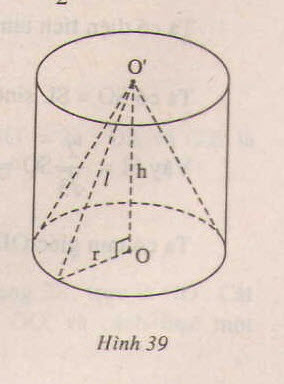
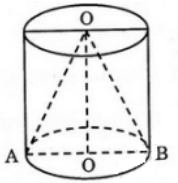
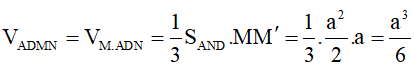Cho đường tròn tâm O bán kính r nằm trên mặt phẳng (P). Từ những điểm M thuộc đường tròn này ta kẻ những đường thẳng vuông góc với (P). Chứng minh rằng những đường thẳng như vậy nằm trên một mặt trụ tròn xoay. Hãy xác định trục và bán kính của mặt trụ đó ?
Bài 1: Khái niệm về mặt tròn xoay
Bài 1 (SGK trang 39)
Thảo luận (1)
Bài 2 (SGK trang 39)
Trong mỗi trường hợp sau đây, hãy gọi tên các hình tròn xoay hoặc khối tròn xoay sinh ra bởi :
a) Ba cạnh của hình chữ nhật khi quay quanh đường thẳng chứa cạnh thứ tư
b) Ba cạnh của một tam giác cân khi quay quanh trục đối xứng của nó
c) Một tam giác vuông kể cả các điểm trong của tam giác vuông đó khi quay quanh đường thẳng chứa một cạnh góc vuông
d) Một hình chữ nhật kể cả các điểm trong của hình chữ nhật đó khi quay quanh đường thẳng chứa một cạnh
Đọc tiếp
Trong mỗi trường hợp sau đây, hãy gọi tên các hình tròn xoay hoặc khối tròn xoay sinh ra bởi :
a) Ba cạnh của hình chữ nhật khi quay quanh đường thẳng chứa cạnh thứ tư
b) Ba cạnh của một tam giác cân khi quay quanh trục đối xứng của nó
c) Một tam giác vuông kể cả các điểm trong của tam giác vuông đó khi quay quanh đường thẳng chứa một cạnh góc vuông
d) Một hình chữ nhật kể cả các điểm trong của hình chữ nhật đó khi quay quanh đường thẳng chứa một cạnh
Thảo luận (1)Hướng dẫn giảiTheo định nghĩa ta thấy kết quả:
a) HÌnh trụ tròn xoay có đường cao là cạnh thứ tư còn bán kính hình trụ bằng độ dài của cạnh kề với cạnh thứ tư đó.
b) Hình nón tròn xoay có chiều cao bằng chiều cao của tam giác cân, cond bán kính đáy bằng một nửađộ dài cạnh đáy của tam giác cân đó.
c) Khối nón tròn xoay.
d) Khối trụ tròn xoay.
(Trả lời bởi Minh Thư)
Bài 3 (SGK trang 39)
Cho hình nón tròn xoay có đường cao h20cm, bán kính đáy r25cm
a) Tính diện tích xung quanh của hình nón đã cho
b) Tính thể tích của khối nón được tạo thành bởi hình nón đó
c) Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12cm. Tính diện tích thiết diện đó ?
Đọc tiếp
Cho hình nón tròn xoay có đường cao \(h=20cm\), bán kính đáy \(r=25cm\)
a) Tính diện tích xung quanh của hình nón đã cho
b) Tính thể tích của khối nón được tạo thành bởi hình nón đó
c) Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12cm. Tính diện tích thiết diện đó ?
Thảo luận (2)Hướng dẫn giải
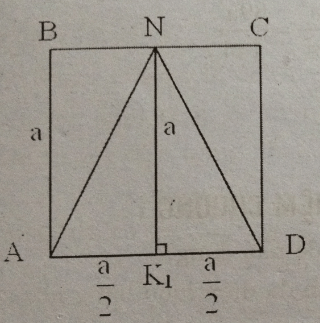
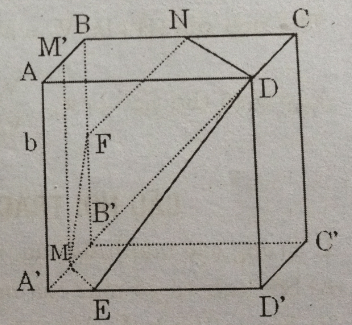
b)-Mặt phẳng (DMN) cắt hình lập phương theo thiết diện MEDNF trong đó ME // ND, FN //DE và chia hình lập phương thành hai khối đa diện (H) và (H’), gọi phần khối lập phương chứa A, B, A’, mặt phẳng (DMN) là (H)
-Chia (H) thành các hình chóp F.DBN, D.ABFMA’ và D.A’EM.
(Trả lời bởi Hai Binh)
Bài 4 (SGK trang 39)
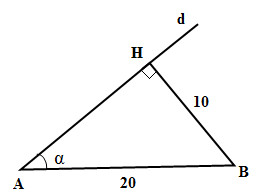
Trong không gian cho hai điểm A, B cố định và có độ dài AB = 20cm. Gọi d là một đường thẳng thay đổi luôn luôn đi qua A và cách B một khoảng bằng 10cm. Chứng tỏ rằng đường thẳng d luôn luôn nằm trên một mặt nón, hãy xác định trục và góc ở đỉnh của mặt nón đó ?
Thảo luận (1)Hướng dẫn giải
Kẻ BH ⊥ d ta có BH = 10cm
Gọi \(\alpha=\widehat{ABH}\)
Ta có: \(\sin\alpha=\dfrac{BH}{AB}=\dfrac{1}{2}\Rightarrow\alpha=30^o\)
Vậy đường thẳng d luôn thuộc mặt nón nhận đường thẳng AB làm trục và có góc ở đỉnh bằng 2α = 60°
(Trả lời bởi Hai Binh)
Bài 5 (SGK trang 39)
Một hình trụ có bán kính đáy \(r=5cm\) và có khoảng cách giữa hai đáy bằng 7cm.
a) Tính diện tích xung quanh của hình trụ và thể tích của khối trụ được tạo nên
b) Cắt khối trụ bởi một mặt phẳn song song với trục và cách trục 3cm. Hãy tính diện tích của thiết diện được tạo nên
Thảo luận (2)Hướng dẫn giải
a) Theo đầu bài, hình trụ có chiều cao h = 7 cm và bán kính đáy r = 5 cm.
Vậy diện tích xung quanh bằng: Sxq= πrh = 35π (cm2)
Thể tích của khối trụ là:
V = πr2h = 175π (cm3)
b) Thiết diện là hình chữ nhật có một cạnh bằng chiều cao của hình trụ bằng 7 cm. Giả sử thiết diện là ABCD.
Ta có AD = 7 cm, OI = 3 cm.
Do tam giác OAI vuông tại A nên
AI2 = OA2 – OI2 = 25 – 9 = 16.
Vậy AI = 4 cm, AB = 8 cm.
(Trả lời bởi Hai Binh)
Bài 6 (SGK trang 39)
Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều cạnh 2a. Tính diện tích xung quanh và thể tích xung quanh và thể tích của hình nón đó ?
Thảo luận (1)Hướng dẫn giải
Bài 7 (SGK trang 40)
Một hình trụ có bán kính r và chiều cao hrsqrt{3}
a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ
b) Tính thể tích khối trụ tạo nên bởi hình trụ đã cho
c) Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng AB và trục của hình trụ bằng 30^0. Tính khoảng cách giữa đường thẳng AB và trục của hình trụ ?
Đọc tiếp
Một hình trụ có bán kính r và chiều cao \(h=r\sqrt{3}\)
a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ
b) Tính thể tích khối trụ tạo nên bởi hình trụ đã cho
c) Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng AB và trục của hình trụ bằng \(30^0\). Tính khoảng cách giữa đường thẳng AB và trục của hình trụ ?
Thảo luận (1)Hướng dẫn giảiTheo công thức ta có:
Sxq = 2πrh = 2√3 πr2
Stp = 2πrh + 2πr2 = 2√3 πr2 + 2 πr2 = 2(√3 + 1)πr2 ( đơn vị thể tích)
b) Vtrụ = πR2h = √3 π r3
c) Giả sử trục của hình trụ là O1O2 và A nằm trên đường tròn tâm O1, B nằm trên đường tròn tâm O2; I là trung điểm của O1O2, J là trung điểm cảu AB. Khi đó IJ là đường vuông góc chung của O1O2 và AB. Hạ BB1 vuông góc với đáy, J1 là hình chiếu vuông góc của J xuống đáy.
Ta có
là trung điểm của
,
= IJ.
Theo giả thiết
= 300.
do vậy: AB1 = BB1.tan 300 =
= r.
Xét tam giác vuông
AB1 = BB1.tan 300 = O1J1A vuông tại J1, ta có:
=
-
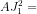
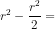
.
Vậy khoảng cách giữa AB và O1O2 :
(Trả lời bởi Minh Thư)
Bài 8 (SGK trang 40)
Một hình trụ có hai đáy là hai hình tròn left(O;rright) và left(O;rright); Khoảng cách giữa hai đáy là OOrsqrt{3}. Một hình nón có đỉnh là O và có đáy là hình tròn left(O;rright)
a) Gọi S_1 là diện tích xung quanh của hình trụ và S_2 là diện tích xung quanh của hình nón, hãy tính tỉ số dfrac{S_1}{S_2} ?
b) Mặt xung quanh của hình nón chia khối trụ thành hai phần, hãy tính tỉ số thể tích hai phần đó ?
Đọc tiếp
Một hình trụ có hai đáy là hai hình tròn \(\left(O;r\right)\) và \(\left(O';r\right)\); Khoảng cách giữa hai đáy là \(OO'=r\sqrt{3}\). Một hình nón có đỉnh là O' và có đáy là hình tròn \(\left(O;r\right)\)
a) Gọi \(S_1\) là diện tích xung quanh của hình trụ và \(S_2\) là diện tích xung quanh của hình nón, hãy tính tỉ số \(\dfrac{S_1}{S_2}\) ?
b) Mặt xung quanh của hình nón chia khối trụ thành hai phần, hãy tính tỉ số thể tích hai phần đó ?
Thảo luận (2)Hướng dẫn giải
Bài 9 (SGK trang 40)
Cắt hình nón đỉnh S bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền bằng asqrt{2}
a) Tính diện tích xung quanh, diện tích đáy và thể tích của khối nón tương ứng
b) Cho dây cung BC của đường tròn đáy hình nón sao cho mặt phẳng (SBC) tạo với mặt phẳng chứa đáy hình nón một góc 60^0. Tính diện tích tam giác SBC ?
Đọc tiếp
Cắt hình nón đỉnh S bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền bằng \(a\sqrt{2}\)
a) Tính diện tích xung quanh, diện tích đáy và thể tích của khối nón tương ứng
b) Cho dây cung BC của đường tròn đáy hình nón sao cho mặt phẳng (SBC) tạo với mặt phẳng chứa đáy hình nón một góc \(60^0\). Tính diện tích tam giác SBC ?
Thảo luận (1)Hướng dẫn giảia) Cạnh huyền chính bằng đường kính đáy do vậy bán kính đáy r =
và đường cao h = r, đwòng sinh l = a.
Vậy Sxq = πrl =
( đơn vị diện tích)
Sđáy =
=
( đơn vị diện tích);
Vnón =
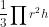
( đơn vị thể tích)
b) Gọi tâm đáy là O và trung điểm cạnh BC là I.
Theo giả thiết,
= 600.
Ta có diện tích ∆ SBC là: S = (SI.BC)/2
Ta có SO + SI.sin600 =
.
Vậy
.
Ta có ∆ OIB vuông ở I và BO = r =
;
OI = SI.cos600 =
.
Vậy BI =
và BC =
.
Do đó S = (SI.BC)/2 =
(đơn vị diện tích)
(Trả lời bởi Minh Thư)
Bài 10 (SGK trang 40)
Cho hình trụ bán kính r và có chiều cao cũng bằng r. Một hình vuông ABCD có hai cạnh AB và CD lần lượt là các dây cung của hai đường tròn đáy, còn cạnh BC và AD không phải là đường sin của hình trụ. Tính diện tích của hình vuông đó và côsin của góc giữa mặt phẳng chứa hình vuông và mặt phẳng đáy ?
Thảo luận (1)Hướng dẫn giảiHạ đường sinh AA1 vuông góc với đáy chứa cạnh CD. Khi đó góc ADA1 là góc giữa hai mặt phẳng hình vuông và mặt đáy.
Vì góc A1DC = 1v nên A1C là đường kính.
Gọi cạnh hình vuông là a.
Ta có
a2 = AD2 = AA12 + A1D2
mà AA1 = h = r, nên ta có:
A1D2 + DC2 = A1C2;
a2 – r2 + a2 = 4r2;
⇒a2=52r2
Vậy diện tích hình vuông là: SABC=a2=52r2 Gọi δ = góc ADA1 là góc tạo bởi mặt phẳng hình vuông và đáy, ta có: sinδ = A1AAD=ra=√25
(Trả lời bởi Minh Thư)